Розробка лекції «Правильні многогранники»

Про матеріал

Тема уроку: «Правильні многогранники». Мета: ознайомити з видами правильних многогранників, розвивати естетичне сприйняття математичних фактів, розширяти кругозір учнів, сприяти пізнанню зв'язків геометрії з природою і літературою, формувати уявлення про красу пов'язаною з симетрією, виховувати критичність мислення, допитливість учня.

Перегляд файлу

Розробка лекції

«Правильні многогранники»

ВИКОНАЛА:

Полозенко К.С.

Тема уроку: «Правильні многогранники».

Мета: ознайомити з видами правильних многогранників, розвивати естетичне сприйняття математичних фактів, розширяти кругозір учнів, сприяти пізнанню зв'язків геометрії з природою і літературою, формувати уявлення про красу пов'язаною з симетрією, виховувати критичність мислення, допитливість учня.

Характеристика змісту:

1) Введення поняття ”Правильний многогранник”. Види правильних многогранників (правильний тетраедр, куб, октаедр, ікосаедр, додекаедр).

2) Формула Ейлера (дослідницька робота класу — підрахувати число вказаних елементів Платонових тіл і занести результати в таблицю; визначити закономірність в зростанні чисел в кожному стовпці).

3) Правильні многогранники в астрономії (система гармонійного пристрою світу І.Кеплера, ядро Землі у формі і з властивістю кристала, що росте), біології (одноклітинні організми — феодарії, форми вірусів), хімії (форма кристалів куховарської солі, монокристал алюмінієво-калієвих квасцов, кристал сірчистого колчедану, молекули метану тощо).

4) Заповнення простору правильними многогранниками (кубом, октаедром і тетраедром, ромбічним додекаедром).

5) Використання правильних многогранників творцями мистецтва (скульпторами, архітекторами, художниками — Леонардо да Вінчі, Сальвадором Далі тощо).

Устаткування: моделі многогранників, репродукція картин С. Далі: “Таємна вечеря”, “У пошуках четвертого виміру”, модель сонячної системи І. Кеплера, ілюстрації ікосаедро-додекаедрової структури землі та правильних многогранників у природі.

Епіграф

"Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".

Л. Керолл

Хід лекції:

Многогранником називається тіло, межа якого є об'єднанням скінченного числа многокутників.

Многогранник називається правильним, якщо

1. він опуклий,

2. всі його грані — рівні правильні многокутники,

3. у кожній вершині сходиться однакове число граней,

4. всі його двогранні кути рівні.

Перші згадки про многогранники відомі ще за три тисячі років до нашої ери в Єгипті і Вавилоні. Але теорія многогранників є і сучасним розділом математики. Вона тісно пов'язана з топологією, теорією графів, має велике значення як для теоретичних досліджень по геометрії, так і для практичних застосувань в інших розділах математики, наприклад, в алгебрі, теорії чисел, прикладній математиці — лінійному програмуванні, теорії оптимального управління. Із найдавніших часів наші уявлення про красу пов'язані з симетрією. Напевно, цим пояснюється інтерес людини до многогранників — дивовижних символів симетрії, що привертали увагу видатних мислителів: Піфагора, Евкліда, Архімеда.

Історія правильних многогранників йде в глибоку старовину. Правильними многогранниками займалися Піфагор і його учні. Їх вражала краса, досконалість, гармонія цих фігур. Пізніше вчення піфагорійців про правильні многогранники виклав в своїх працях інший старогрецький учений, філософ — ідеаліст Платон. З тих пір правильні многогранники почали називатися платоновими тілами.

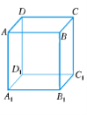
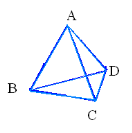
Існує п'ять видів правильних многогранників (назви їх прийшли з Греції): тетраедр, гексаедр (куб), октаедр, додекаедр, ікосаедр. Чому 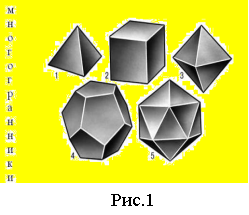правильні многогранники отримали такі імена? Це пов'язано з числом їх граней. Тетраедр (1) має 4 грані, в перекладі з грецького "тетра" — чотири, "едрон" — грань. Гексаедр (куб) (2) має 6 граней, "гекса" — шість; октаедр (3) — восьмигранник, "окто" — вісім; додекаедр (4) — дванадцятигранник, "додека" — дванадцять; ікосаедр (5) має 20 граней, "ікоси" — двадцять (рис.1).

Перший, хто звернув увагу на топологічні властивості (число граней, вершин і ребер) многогранників і займався їх вивченням, був Л. Ейлер. Многогранники виділяються незвичайними властивостями, найяскравіше з яких формулюється в теоремі Ейлера про число граней, вершин і ребер опуклого многогранника: для будь-якого опуклого многогранника справедливе співвідношення Г+В-Р=2, де Г-число граней, В-число вершин, Р-число ребер даного многогранника.

Повідомлення: «Правильні многогранники у філософській картині світу Платона».

Платон вважав, що світ будується з чотирьох «стихій» — вогню, землі, повітря і води, а атоми цих «стихій» мають форму чотирьох правильних многогранників. Тетраедр втілював вогонь, оскільки його вершина спрямована вгору, як у полум'я, що розгорілося; ікосаедр — як самий обтічний — воду; куб — найстійкіша з фігур — землю, а октаедр — повітря. У наш час цю систему можна порівняти з чотирма станами речовини — твердим, рідким, газоподібним і полум'яним. П'ятий многогранник — додекаедр символізував весь світ і вважався найголовнішим (рис.2). Вже по латині в середні віки його стали називати «п'ята суть» або guinta essentia, «квінта есенція», звідси з’явилося цілком сучасне слово «квінтесенція», що означає все найголовніше, основніше, дійсну суть чого-небудь.

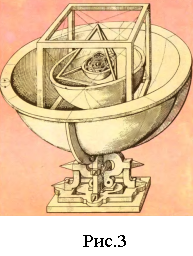А зараз від Стародавньої Греції перейдемо до Європи XVI — XVII вв., коли жив і творив чудовий німецький астроном, математик Іоганн Кеплер (1571 — 1630). Важливе місце займали правильні многогранники в системі гармонійного пристрою світу І. Кеплера (рис.3). Все та ж віра в гармонію, красу і математично закономірний пристрій всесвіту привела І. Кеплера до думки про те, що оскільки існує п'ять правильних многогранників, то їм відповідають тільки шість планет. На його думку, сфери планет зв'язані між собою вписаними в них платоновими тілами. Оскільки для кожного правильного многогранника центри вписаної і описаної сфер співпадають, то вся модель матиме єдиний центр, в якому знаходитиметься Сонце. Виконавши величезну обчислювальну роботу, в 1596 р. І. Кеплер в книзі "Тайна мироздания" опублікував результати свого відкриття. У сферу орбіти Сатурну він вписує куб, в куб — сферу Юпітера, в сферу Юпітера — тетраедр, і так далі послідовно вписуються один в одного сфера Марса — додекаедр, сфера Землі — ікосаедр, сфера Венери — октаедр, сфера Меркурія. Таємниця всесвіту здається відкритою. Сьогодні ж можна з упевненістю сказати, що відстані між планетами не пов'язані ні з якими многогранниками. Втім, можливо, що без " Тайна мироздания ", "Гармонии мира" І.Кеплера, правильних многогранників не було б трьох знаменитих законів І.Кеплера, які грають важливу роль в описі руху планет.

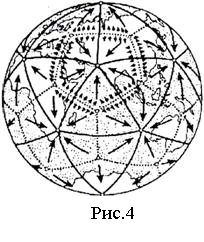Ідеї Піфагора, Платона, І.Кеплера про зв'язок правильних многогранників з гармонійним пристроєм світу вже у наш час знайшли своє продовження в цікавій науковій гіпотезі, авторами якої (на початку 80-х років) з'явилися московські інженери В.Макаров і В.Морозов. Вони вважають, що ядро Землі має форму і властивості кристала, що росте, надає дію на розвиток всіх природних процесів, що йдуть на планеті. Промені цього кристала, а точніше, його силове поле, обумовлюють ікосаедро-додекаедрову структуру Землі(рис.4), що виявляється в тому, що в земній корі як би проступають проекції вписаних в земну кулю правильних многогранників: ікосаедра і додекаедра. Їх 62 вершини і середина ребер, званих авторами вузлами, володіють певними специфічними властивостями, що дозволяють пояснити деякі незрозумілі явища. Якщо нанести на глобус вогнища найбільш крупних і примітних культур і цивілізацій Стародавнього світу, можна відмітити закономірність в їх розташуванні щодо географічних полюсів і екватора планети. Багато покладів корисних копалини тягнуться уподовж ікосаедро-додекаедрової сітки. Ще дивовижніші речі відбуваються в місцях перетину цих ребер: тут розташовуються вогнища найдавніших культур і цивілізацій: Перу, Північна Монголія, Гаїті, Обська культура тощо. У цих точках спостерігаються максимуми і мінімуми атмосферного тиску, гігантські завихрення Світового океану, тут шотландське озеро Лох-несс, Бермудський трикутник. Подальші дослідження Землі, можливо, визначать відношення до цієї красивої наукової гіпотези, в якій, як видно, правильні многогранники займають важливе місце.

Де ще можна побачити ці дивовижні тіла? У дуже красивій книзі німецького біолога початку нашого століття Е.Геккеля "Красота форм в природе" можна прочитати такі рядки: "Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы". Створення природи, наведені в цій книзі, красиві і симетричні. Це невіддільна властивість природної гармонії. Але тут видно і одноклітинні організми — феодарії (рис.5), форма яких точно передає ікосаедр. Чим же викликана така природна геометризація? Можливо, тим, що зі всіх многогранників з такою ж кількістю граней саме ікосаедр має найбільший об’єм і найменшу площу поверхні. Це геометрична властивість допомагає морському мікроорганізмові долати тиск водної товщі.

Цікаво і те, що саме ікосаедр опинився в центрі уваги біологів в їх суперечках щодо форми вірусів. Вірус не може бути досконало круглим, як вважалося раніше. Щоб встановити його форму, брали різні многогранники, направляли на них світло під тими ж кутами, що і потік атомів на вірус. Виявилось, що тільки один многогранник дає таку саму тінь — ікосаедр. Його геометричні властивості, про які мовилося вище, дозволяють економити генетичну інформацію.

Правильні многогранники — найвигідніші фігури. І природа цим широко користується. Кристали деяких знайомих нам речовин мають форму правильних многогранників. Так, куб передає форму кристалів куховарської солі NaСl (рис.6), монокристал алюмінієво-калієвих квасцов (KAlSO4)₂12H2O має форму октаедра, кристал сірчистого колчедану FeS має форму додекаедра (рис.7), сурм'янистий сірчанокислий натрій — тетраедра, бор — ікосаедра. Правильні многогранники визначають форму кристалічних решіток деяких хімічних 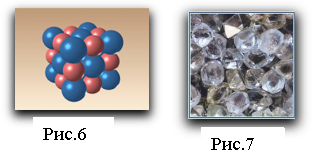речовин.

Велику цікавість до форм правильних многогранників проявляли також скульптори, архітектори, художники. Їх всіх вражала досконалість, гармонія многогранників.

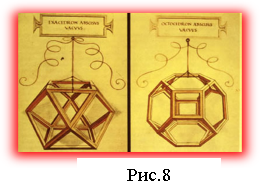
Леонардо да Вінчі (1452 — 1519) захоплювався теорією многогранників і часто зображав їх на своїх полотнах. Наприклад на його ілюстрації до книги Луки Пачолі (самого відомого бухгалтера) (рис.8).

Сальвадор Далі (1904—1989) використовував додекаедр у своїх роботах. Наприклад у картині “У пошуках четвертого виміру” він намалював цей многогранник на передньому плані (рис.9). У картині “Таємна вечеря” зобразив І.Христа зі своїми учнями на тлі величезного прозорого додекаедра (рис.10).

Моріс Ешер у своїй метаморфозі “Рептилії” (літографія, 1943 г) зобразив додекаедр (рис.11).

На надгробному пам'ятнику в кафедральному соборі Солсбері теж можна побачити правильні многогранники (рис.12).

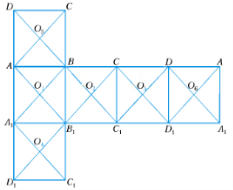
І ще одне питання виникає у зв'язку з правильними многогранниками: чи можна ними заповнити простір так, щоб між ними не було просвітів? Він виникає по аналогії з правильними багатокутниками, деякими з яких можна заповнити площину. Виявляється, заповнити простір можна тільки за допомогою одного правильного многогранника — куба.

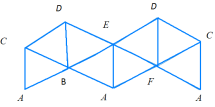
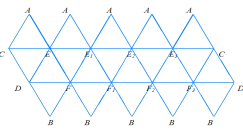
Цікаво відмітити, що правильними тетраедрами і октаедрами теж можна заповнити простір, якщо розмістити їх так, як показано на рисунку 13.[10, 31]

Простір можна заповнити і ромбічними додекаедрами (ріс.14). Щоб це зрозуміти, треба вирішити задачу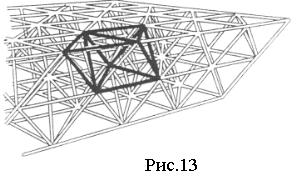: за допомогою семи кубів, які утворюють просторовий "крест" (рис.14), побудуйте ромбододекаедр і покажіть, що ними можна заповнити простір.

Розв’язання. Кубами можна заповнити простір. Розглянемо частину кубічних решіток. Середній куб залишимо незайманим, а в кожному з "оздоблюючих" кубів проведемо площини через всі шість пар протилежних ребер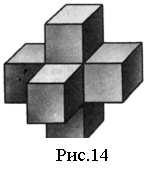. При цьому "оздоблюючі" куби розіб'ються на шість рівних пірамід з квадратними підставами і бічними ребрами, рівними половині діагоналі куба. Піраміди, що примикають до незайманого куба, і утворюють разом з останнім ромбічний 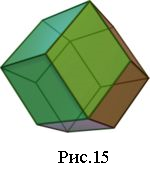додекаедр(рис.15). Звідси зрозуміло, що ромбічними додекаедрами можна заповнити весь простір. Як наслідок отримуємо, що об'єм ромбічного додекаедра дорівнює подвоєному об'єму куба, ребро якого співпадає з меншою діагоналлю грані додекаедра.

Вирішивши задачу, ми прийшли до ромбічних додекаедрів. Цікаво, що бджолині осередки (рис.16), які також заповнюють простір без просвітів, також є в ідеалі геометричними фігурами. Верхня частина бджолиного осередку є частиною ромбододекаедра.

Отже, правильні многогранники відкрили нам спроби учених наблизитися до таємниці світової гармонії і показали чарівну привабливість геометрії.

Цікаві задачі

1.Як розрізати запечатаний конверт (рис.17) і скласти з нього тетраедр?

(На обох сторонах конверту — у одного і того ж краю, накреслити рівносторонній трикутник і розрізати по пунктирній прямій. Права його половина не потрібна, а ліву перегнути по сторонам трикутника — на обох сторонах конверта, і сумістимо точки А та В. Тетраедр готовий!)

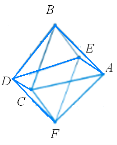
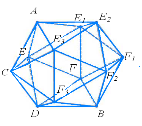
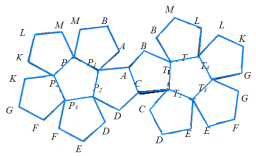
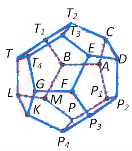
2.Муха, розгулюючи по 12 ребрам ікосаедра, проповзає по кожному з них принаймні один раз. Який найменший шлях повинна пройти муха, щоб побувати на всіх ребрах ікосаедра?(Рішенню задачі може допомогти проекція ікосаедра на площину рис.18)

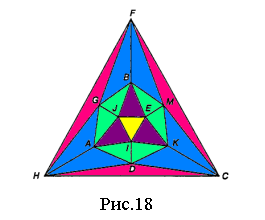(Найкоротша відстань, яку повинна подолати муха для того, щоб побувати на всіх ребрах ікосаедра, рівна 35 одиницям (одиниця — довжина ребра ікосаедра). Стерши п'ять ребер ікосаедра (наприклад, ребра FM, BE, JA, ID і HC), ми отримаємо непарне число ребер, що сходяться тільки в двох точках G і K. Тому муха їх може обійти (почавши свій шлях в точці G і закінчивши в точці K), пройшовши по кожному ребру лише один раз. Пройдена мухою відстань рівна 25 одиницям. Це найдовший шлях, всі ділянки якого муха проходить по одному разу. Якщо муха на своєму шляху зустрічає стерті ребра, ми просто додаємо їх до шляху з G в K, вважаючи, що муха проходить їх двічі (у протилежних напрямах). П'ять стертих ребер, по яким проходить двічі, складають ще 10 одиниць до вже пройденого шляху. В сумі це дасть 35одиниць.)

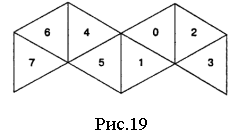3.Усі п'ять платонових тіл використовувалися як гральні кості. Після куба найбільшу популярність придбали гральні кості у формі октаедра. Як зробити таку кость, показано на рисунку 19. Накресливши і вирізавши смужку і перенумерувавши грані, її перегинають уздовж ребер, а «відкриті» ребра склеюють прозорою стрічкою. Виходить мініатюрний октаедр (рис.20). Сума очок на протилежних гранях октаедричної гральної кості, як і у звичайної кубічної, дорівнює семи. За бажання за допомогою нової кості ви можете показати фокус з відгадуванням задуманного числа. Попросіть кого-небудь загадати будь-яке число від 0 до 7. Покладете октаедр на стіл так, щоб той, що загадав міг бачити тільки грані з цифрами 1, 3, 5 і 7, і запитаєте, чи не бачить він задуманого ним числа. Якщо він відповідає ствердно, ви запам’ятовуєте про себе число 1. Потім ви перевертаєте октаедр так, щоб тому хто загадує були видні грані з цифрами 2, 3, 6 і 7, і знову ставите те ж питання. Цього разу ствердна відповідь означає, що ви повинні запам'ятати число 2. У третій (і останній раз) ви повторюєте своє питання, повернувши октаедр так, щоб той, що загадав міг бачити грані з цифрами 4, 5, 6 і 7. Ствердна відповідь в цьому випадку оцінюється числом 4. Склавши оцінки всіх трьох відповідей, ви отримаєте задумане вашим приятелем число. Щоб легко було відшукати потрібні положення октаедра, абияк помітьте три вершини, які повинні бути повернуті до вас, коли ви стоїте обличчям до глядача (що задумав число).