Розробка показового уроку: "Двогранний кут"

Про матеріал

Формувати поняття двогранного кута та кута між площинами, ребра і грані двогранного кута, лінійного кута двогранного кута, сформувати вміння розвя'зувати задачі, що передбачають використання цих понять.

Зміст архіву

ñó«úαá¡¡¿⌐ ¬πΓ.docx docx
двогранні кути.pptx pptx

Перегляд файлу

Урок

Тема уроку. Двогранний кут. Лінійний кут двогранного кута.

Формування компетентностей:

предметна компетентність: формувати поняття двогранного кута та кута між площинами, ребра і грані двогранного кута, лінійного кута двогранного кута, сформувати вміння розвя'зувати задачі, що передбачають використання цих понять;
ключові компетентності:
математична компетентність - оперувати геометричними об'єктами на площині та в просторі;
ініціативність і підприємливість - аргументувати та захищати свою позицію, дискутувати;
обізнаність та самовираження у сфері культури - унаочнювати математичні моделі;

Тип уроку: засвоєння нових знань і вмінь.

Обладнання та наочність: стереометричний набір, моделі многогранників
, комп'ютер, проектор, підручник, таблиці, аркуші паперу.

Методи і прийоми навчання: вправа "складанка", метод «Чиста дошка», гра «Ромашка», проблемне питання , випереджуюче завдання, робота в парах, математичне лото, групова робота, метод незакінченого речення, гра «Математичний футбол»

Хід уроку

І. Організаційний етап.Розминка

Вправа «Складанка»:

Із розсипаних слів складіть народну приказку: «навчати, добре, знати, хто, хоче, все, того».

(Відповідь – добре того навчати, хто хоче все знати).

ІІ. Актуалізація опорних знань.

Розгадування кросворду

https://learningapps.org/display?v=p3akqxqnv19

Групова робота

Мета: перевірити навички та вміння учнів виконувати завдання з теми:"Перпендикуляр і похила до площини"

Завдання: учні повинні розв’язати завдання та заповнити таблицю на листках і здати на перевірку.

Слово вчителя – ви вже об'єднанні в 2 групи, пригадаємо правила роботи в групах: - вмійте слухати; - не критикуйте; - вносьте свій вклад в результат роботи групи; - будьте дружними; - допомагайте іншим. В кожній групі оберіть керівника, який буде організовувати порядок виконання завдання, підбивати підсумки роботи, визначати доповідача. Я роздаю вам конверти з завданнями.

І - група

АВ- перпендикуляр, АС - похила, ВС - проекція похилої, α - кут між перпендикуляром та похилою. Заповніть таблицю.

АВ			6 см
ВС		4 см
АС	6 см	8 см	12 см
α	30⁰

ІІ - група

АВ		7 см	14 см
ВС	5 см		14 см
АС	10 см
α		60⁰

ІІІ. Вивчення нового матеріалу.

Формулювання теми, мети й завдань уроку, мотивація навчальної діяльності.

Ми весь час проводимо аналогію між поняттями в планіметрії та стереометрії. Сьогодні на уроці ми згадували, що називають кутом в планіметрії та кутом між площинами в стереометрії. Навіть в класній кімнаті ми можемо побачити кути між площинами.

А тепер давайте перегорнемо по прямій аркуш паперу.

Проблемне питання

Яку фігуру ми отримали?

 Сприйняття та усвідомлення матеріалу

План вивчення теми

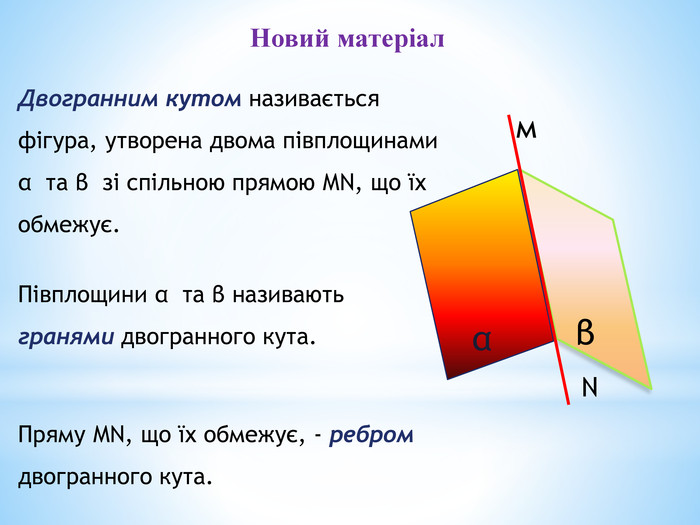
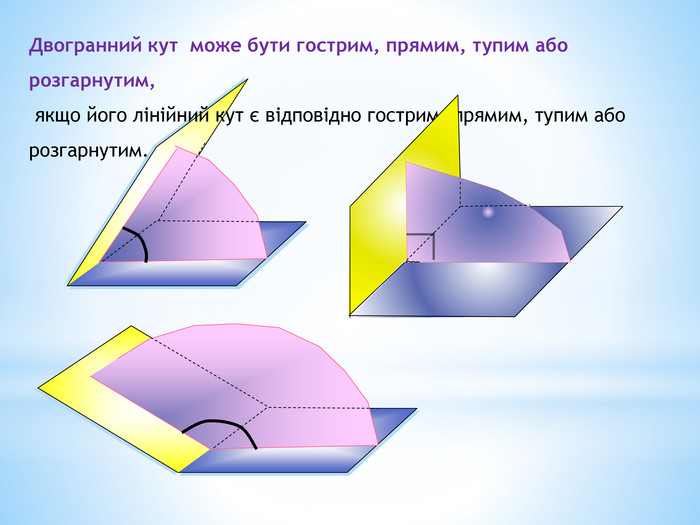
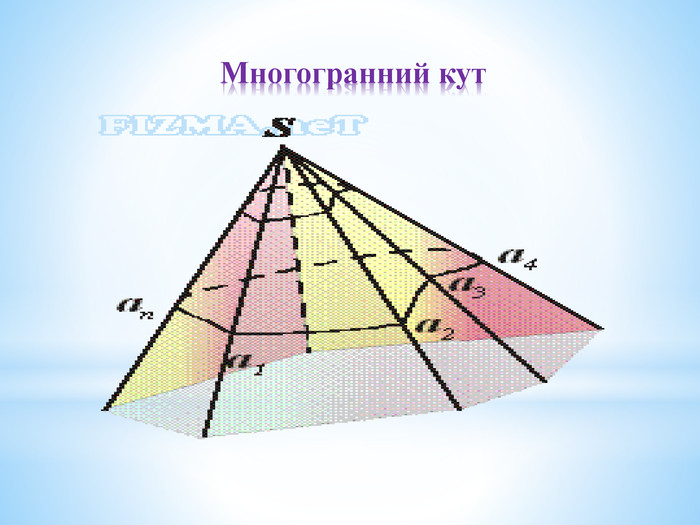
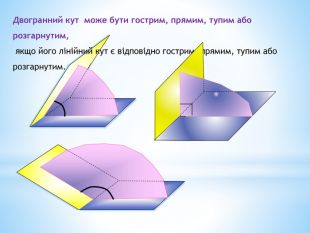
1. Означення двогранного кута.

2. Грані та ребро двогранного кута.

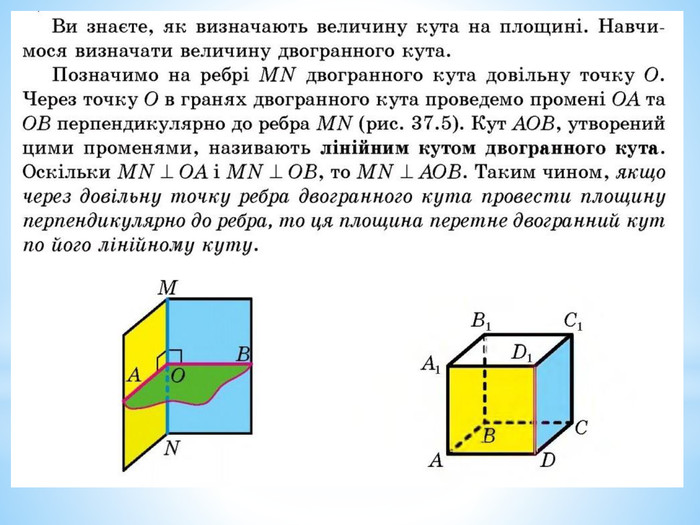
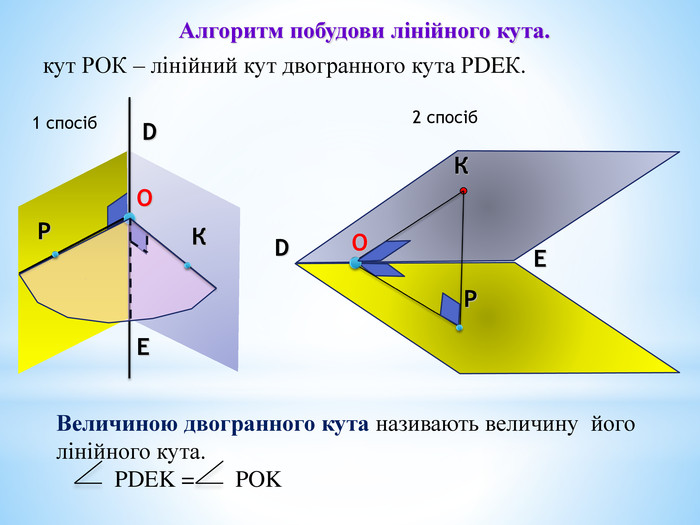
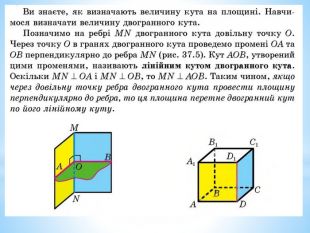
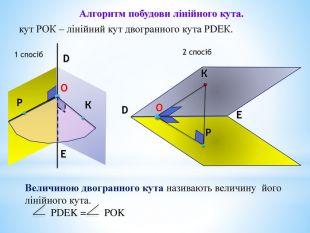
3. Лінійний кут двогранного кута.

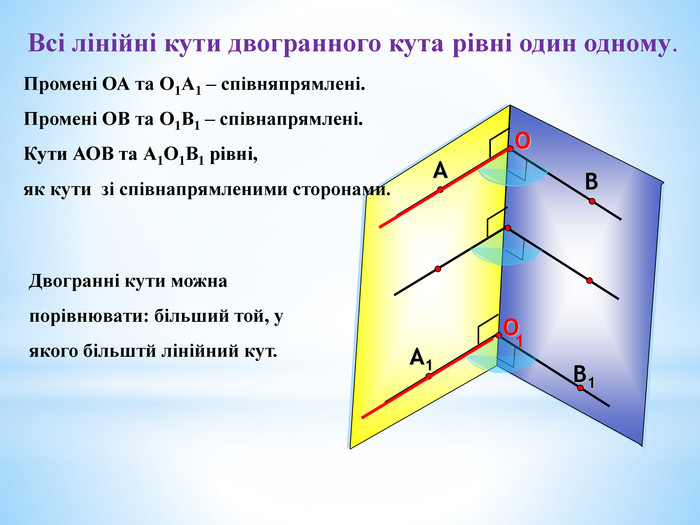
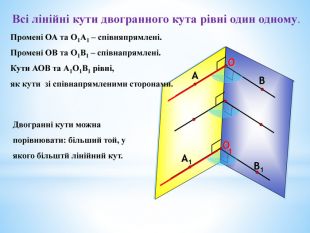
4. Рівність усіх лінійних кутів двогранного кута.

5. Градусна міра двогранного кута.

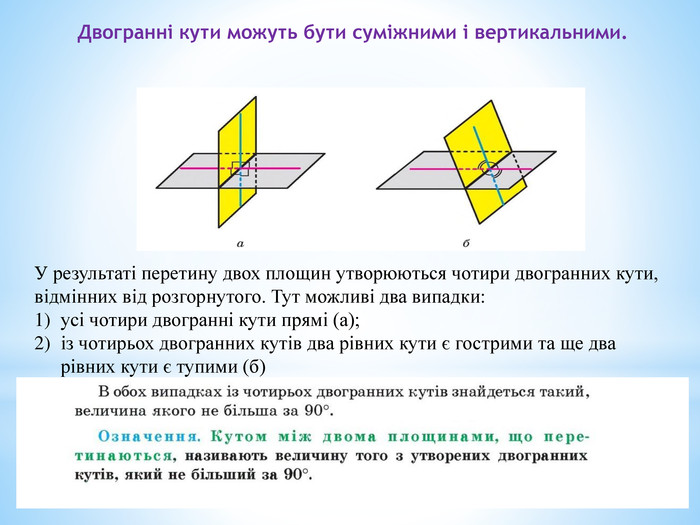
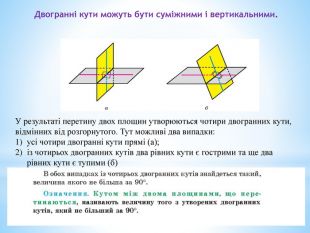
6. Кут між двома площинами.

7. Приклади двогранного кута із навколишнього середовища.

ІV. Засвоєння нових знань і способів дій

Виконання вправ

1.За допомогою стереометричного набору змоделюйте двогранний кут.

2.Покажіть на моделях многогранників та з оточення двогранні кути, вкажіть їх елементи (ребра, грані).

Колективне розв’язування

Два рівнобедрених трикутники АВС і АВD зі спільною основою АВ утворюють двогранний кут, величина якого 60. Знайдіть відстань СD між вершинами цих трикутників, якщо АВ=16 см, AD=BD=17 cм, кут АСВ= 90.(13 см)

ІV. Застосування нових знань і вмінь

Робота в парах

Обговоріть план виконання завдань. Розподіліть, хто виконуватиме завдання варіанту І, а хто - варіанту ІІ. Виконайте завдання і здійсніть взаємоперевірку. Здайте роботу вчителеві на перевірку.

Варіант - І	Варіант - ІІ
1) OD - перпендикуляр до площини прямокутника ABCD. Побудуйте лінійний кут двогранного кута між площинами.
ОВС і АВС	ОАВ і АВС
На одній із граней двогранного кута позначено точку М, із якої проведено перпендикуляр МА до ребра кута і перпендикуляр МВ до другої грані. Обчисліть градусну міру цього кута, якщо:
МА = 8 см, МВ = 4 см	МА = см, МВ = 2 см

VII. Підбиття підсумків уроку.Рефлексія.

Бліцопитування:

Скільки двогранних кутів утвориться при перетині двох площин?
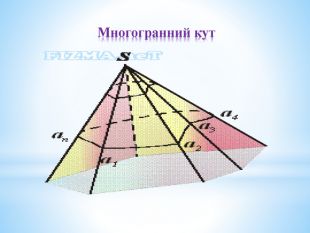
Чи існує опуклий чотиригранний кут, всі плоскі кути якого дорівнюють 90?
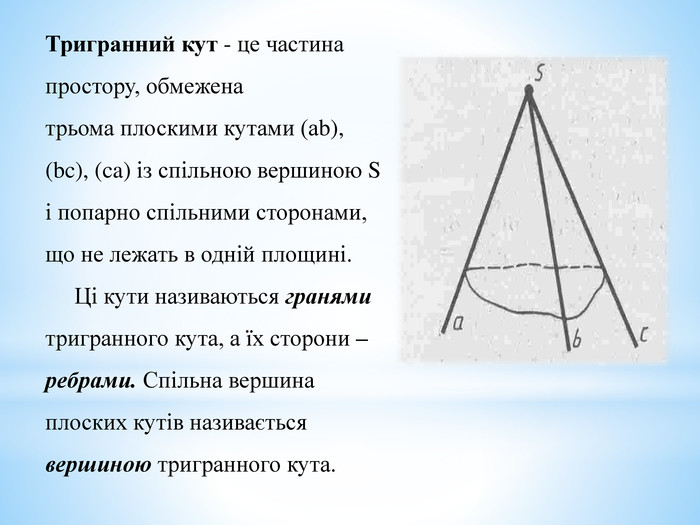
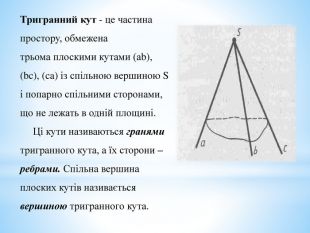
Скільки тригранних кутів має трикутна піраміда? Куб?

Рефлексія

Метод незакінченого речення
На сьогоднішньому уроці я дізнався …
Я зрозумів…
Я вмію…
Я забув, але пригадав…

VIII. Домашнє завдання.

Завдання за підручником: §37, №37.5, питання ст. 202.
Додаткове завдання.

Кут між площинами трикутників АВС і DВС дорівнює 60⁰. Знайдіть довжину відрізка АD, якщо АВ =15 см, ВС = 14 см, АС = 13 см, DВ = DС = 9 см. (Відповідь. 4см.)

Перегляд файлу

Попередній слайд 1 / 18 Наступний слайд

Зміст слайдів

Номер слайду 1

Двогранний кут

Номер слайду 2

Епіграф. Те, що я чую, я забуваю. Те, що я бачу, я пам’ятаю. Те, що я роблю, я розумію. Конфуцій.

Номер слайду 3

ІV. Вивчення нового матеріалу. Формулювання теми, мети й завдань уроку, мотивація навчальної діяльності. Ми весь час проводимо аналогію між поняттями в планіметрії та стереометрії. Сьогодні розгадуючи кросворд ми згадували кути та їх види. Кути розглядаються, як в просторі так і на площині, як між прямими так і між площинами. Навіть в класній кімнаті ми можемо побачити кути між площинами. А тепер давайте перегорнемо по прямій аркуш паперу. Яку фігуру ми отримали? Сьогодні ми поговоримо про просторову фігуру, яку називають двогранним кутом.

Номер слайду 4

αβм. NДвогранним кутом називається фігура, утворена двома півплощинами α та β зі спільною прямою МN, що їх обмежує. Півплощини α та β називають гранями двогранного кута. Пряму МN, що їх обмежує, - ребром двогранного кута. Новий матеріал

Номер слайду 5

Наочне представлення

Номер слайду 6

Номер слайду 7

кут РОК – лінійний кут двогранного кута РDEК. DEВеличиною двогранного кута називають величину його лінійного кута. PDEK = POKАлгоритм побудови лінійного кута. DEOКOРК1 спосіб2 спосіб. Р

Номер слайду 8

Всі лінійні кути двогранного кута рівні один одному. АВOА1 В1 O1 Промені ОА та О1 А1 – співняпрямлені. Промені ОВ та О1 В1 – співнапрямлені. Кути АОВ та А1 О1 В1 рівні, як кути зі співнапрямленими сторонами. Двогранні кути можна порівнювати: більший той, у якого більштй лінійний кут.

Номер слайду 9

Двогранний кут може бути гострим, прямим, тупим або розгарнутим, якщо його лінійний кут є відповідно гострим, прямим, тупим або розгарнутим.

Номер слайду 10

Двогранні кути можуть бути суміжними і вертикальними. У результаті перетину двох площин утворюються чотири двогранних кути, відмінних від розгорнутого. Тут можливі два випадки:усі чотири двогранні кути прямі (а);із чотирьох двогранних кутів два рівних кути є гострими та ще два рівних кути є тупими (б)

Номер слайду 11

Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двагранні кути, називається бісекторною півплощиною, або бісектором двогранного кута.

Номер слайду 12

Тригранний кут - це частина простору, обмежена трьома плоскими кутами (аb), (bc), (ca) із спільною вершиною S і попарно спільними сторонами, що не лежать в одній площині. Ці кути називаються гранями тригранного кута, а їх сторони – ребрами. Спільна вершина плоских кутів називається вершиною тригранного кута.

Номер слайду 13

Многогранний кут

Номер слайду 14

За допомогою стереометричного набору змоделюйте двогранний кут. Покажіть на моделях многогранників та з оточення двогранні кути, вкажіть їх елементи (ребра, грані). Колективне розв’язування Два рівнобедрених трикутники АВС і АВD зі спільною основою АВ утворюють двогранний кут, величина якого 60. Знайдіть відстань СD між вершинами цих трикутників, якщо АВ=16 см, AD=BD=17 cм, кут АСВ= 90. (13 см)Закріплення вивченого матеріалу.

Номер слайду 15

Варіант - ІВаріант - ІІ1) OD - перпендикуляр до площини прямокутника ABCD. Побудуйте лінійний кут двогранного кута між площинами. ОВС і АВСОАВ і АВСНа одній із граней двогранного кута позначено точку М, із якої проведено перпендикуляр МА до ребра кута і перпендикуляр МВ до другої грані. Обчисліть градусну міру цього кута, якщо: МА = 8 см, МВ = 4 см. МА = см, МВ = 2 см. Робота в парах. Обговоріть план виконання завдань. Розподіліть, хто виконуватиме завдання варіанту І, а хто - варіанту ІІ. Виконайте завдання і здійсніть взаємоперевірку. Здайте роботу вчителеві на перевірку.

Номер слайду 16

Домашнє завдання: § 37, №37.5, відповідати на питання ст. 202. Додаткове завдання. Кут між площинами трикутників АВС і DВС дорівнює 600. Знайдіть довжину відрізка АD, якщо АВ =15 см, ВС = 14 см, АС = 13 см, DВ = DС = 9 см.