Розробка програми для порівняння графів на еквівалентність
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Національний аерокосмічний університет ім. М.Є. Жуковського
“Харківський авіаційний інститут”
Кафедра комп’ютерних систем, мереж і кібербезпеки
Звіт з ознайомчої практики
«Розробка програми для порівняння графів на еквівалентність»
Харків – 2022
План
2. Обгрунтування розробки та порівняльний аналіз аналогів
4. Об'єкт, предмет, мета, завдання дослідження
5. Вимоги до продукта.........................................................4
7. Верифікація.................................................................9
Результати тестів............................................................10
8. Висновки...................................................................26
9. Знання та навички, отримані при проходженні практики.................27
Додаток А. Настанова оператору.............................................28
1 Призначення програми....................................................28
2 Технічні засоби для запуску програми.....................................28
3 Завантаження та робота з даною програмою...............................28
Додаток Б. Вихідні тексти програми..........................................31
Програма....................................................................31
Юніт-тести...................................................................51
1. Формулювання завдання
Під час проходження практики буде зроблено основні вимоги до програмного засобу, який я розробляв раніше. Я вибрав такий програмний засіб: додаток для роботи з неорієнтованими графами.
2. Обґрунтування розробки та порівняльний аналіз аналогів
Є багато додатків та сайтів в яких можна будувати графи але в них немає достатнього функціоналу для роботи з графами.
Сайт який я використовував для побудови графів: «Graph Editor» - https://csacademy.com/app/graph_editor;
«Graph Editor» рис. 2.1. Цей сайт дуже зручний, в ньому є два варіанти додавання ребер (орієнтований, неорієнтований), а також є декілька режимів побудови графа та функція завантаження зображення графа у форматі png. Слід зазначити, що інтерфейс даного сайту простий і користуватися ним зручно.
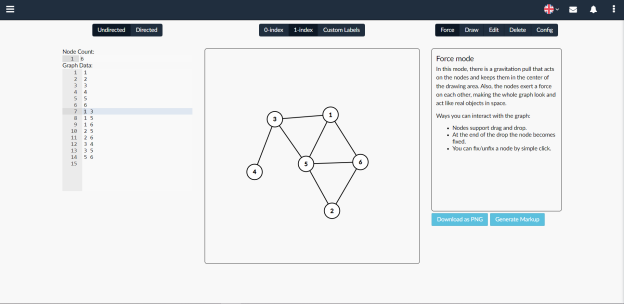
Рисунок 2.1 - Сайт «Graph Editor»
Таблиця 2.1 – Порівняння додатку з вже існуючим сайтом
|
Характеристика |
Сайт |
Мій додаток |
|
Побудова неорієнтованих графів |
Є така можливість |
Є така можливість |
|
Побудова орієнтованих графів |
Є така можливість |
Неможливо |
|
Визначення матриць графів |
Неможливо |
Є така можливість |
|
Визначення ланцюгів та циклів графа |
Неможливо |
Є така можливість |
|
Побудова двох графів |
Неможливо |
Є така можливість |
|
Зчитання графів з текстового файлу |
Неможливо |
Є така можливість |
|
Зберігання зображення графа |
Є така можливість |
Є така можливість |
|
Побудова графа з клавіатури |
Є така можливість |
Неможливо |
|
Порівняння двох графів за характеристикою: біхроматичність (двудольність) графа |
Неможливо |
Є така можливість |
3. Актуальність:
- Дуже важко знайти додаток або сайт для роботи з графами, який має достатньо потрібних функцій;
- Багато людей працюють з графами, тому важливо створити зручний та якісній додаток;
- Теорія графів швидко розвивається і знаходить все більше і більше застосування. Теорія графів містить велику кількість невирішених проблем і поки не доведених гіпотез.
4. Об'єкт, предмет, мета, завдання дослідження
Мета дослідження полягає в тому щоб створити продукт, який буде виконувати певні дії з графами та буде допомагати у вивченні «Теорії графів».
Завдання дослідження. Даний проект присвячений роботі з неорієнтованими графами. Визначенню чи являються графи біхроматичними (двудольними).
Об’єкт дослідження – неорієнтовані графи.
Предмет дослідження – додаток для роботи з неорієнтованими графами.
5. Вимоги до продукта
Таблиця 5.1 – Бізнес-вимоги
|
№ |
Вимога |
Acceptance criteria |
|
1 |
Потрібен зручний та якісний додаток для роботи з графами |
Використання WindowsForm для графічного представлення додатку |
|
2 |
Потрібна функція порівняння графів на еквівалентність за такою характеристикою: біхроматичність (двудольність). Даної функції немає в жодному додатку для роботи з графами. |
В додатку потрібна можливість створення двох графів |
|
3 |
Потрібна функція для створення графа з текстового документу. |
Задання графа повинно бути у форматі MFO |
Таблиця 5.2 – Користувацькі вимоги
|
№ |
Вимога |
Acceptance criteria |
Результат |
|
1 |
Створення вершин та ребер графа |
Кількість вершин не більше 20, кількість ребер не більше 50 Мають бути відповідні кнопки |
Реалізовано |
|
2 |
Видалення вершин та ребер графа |
Має бути відповідна кнопка |
Реалізовано |
|
3 |
Повне видалення графа |
Має бути відповідна кнопка |
Реалізовано |
|
4 |
Виведення матриць |
Мають бути відповідні кнопки |
Реалізовано |
Продовження таблиці 5.2
|
5 |
Виведення ланцюгів та циклів графа |
Мають бути відповідні кнопки |
Реалізовано |
|
6 |
Створення графу з текстового документу |
Має бути відповідна кнопка |
Реалізовано |
|
7 |
Переключення між графами 1 та 2 |
Має бути відповідна кнопка |
Реалізовано |
|
8 |
Зберігання графа |
Має бути відповідна кнопка |
Реалізовано |
|
9 |
Визначення двудольність графів та порівняння графів на еквівалентність |
Має бути відповідна кнопка |
Реалізовано |
Таблиця 5.3 – Функціональні вимоги
|
№ |
Вимога |
Acceptance criteria |
|
1 |
Додаток не потрібно інсталювати |
Запуск додатку відбувається через .exe файл |
|
2 |
Після видалення вершини графа, нумерація вершин змінюється програмою автоматично |
Немає критерій |
Таблиця 5.4 – Нефункціональні вимоги
|
№ |
Вимога |
Acceptance criteria |
|
1 |
Місце на накопичувачі щонайменше 1 MB |
Запуск додатку відбувається через exe файл |
|
2 |
Обсяг оперативної пам’яті щонайменше 500 MB |
Немає критерій |
6. Діаграми
Для створення діаграм я використовував додаток Visio
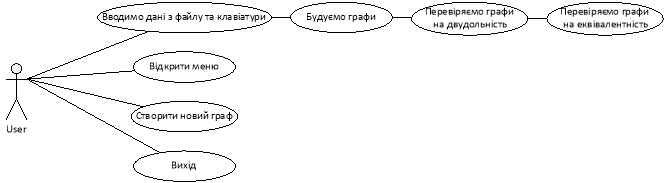
Рисунок 6.1 – UML діаграма варіантів використання (діаграма прецедентів)
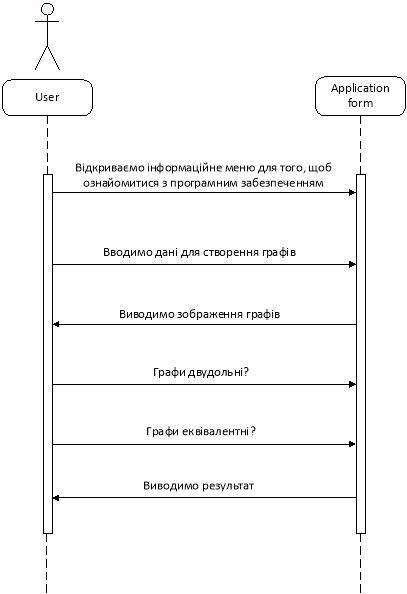
Рисунок 6.2 – Діаграма послідовності
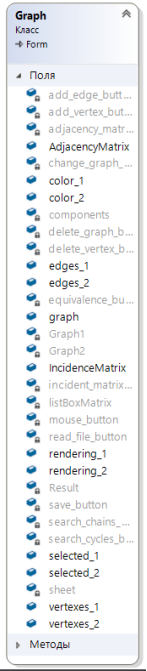
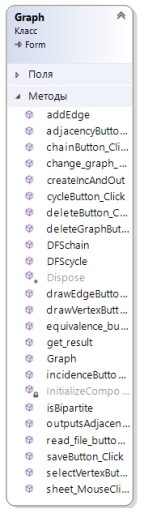
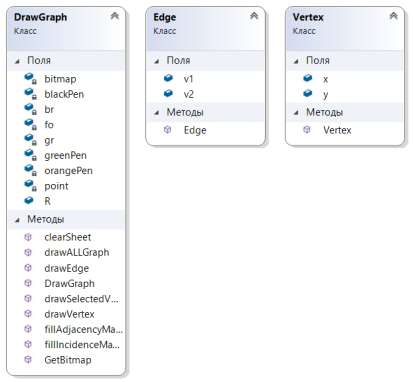
Рисунок 6.3 – Діаграма класів
7. Верифікація
Таблиця 7.1 – Верифікація
|
№ |
Заголовок |
Реалізація |
Висновок |
|
1 |
Візуальне представлення графів |
drawVertex drawEdge drawALLGraph |
Реалізовано |
|
2 |
Додавання вершин графа |
vertexes_1.Add vertexes_2.Add |
Реалізовано |
|
3 |
Додавання неорієнтованих ребер графа |
addEdge |
Реалізовано |
|
4 |
Видалення вершин графа |
deleteButton_Click |
Реалізовано |
|
5 |
Видалення ребер графа |
deleteButton_Click |
Реалізовано |
|
6 |
Виведення матриці суміжності графів |
outputsAdjacency |
Реалізовано |
|
7 |
Виведення матриць інцидентності графів |
outputsIncidence |
Реалізовано |
|
8 |
Ввод даних з клавіатури та з текстового файлу |
read_file_button_Click |
Реалізовано |
|
9 |
Виведення елементарних ланцюгів |
DFSchain |
Реалізовано |
|
10 |
Виведення елементарних циклів |
DFScycle |
Реалізовано |
|
11 |
Зберігання графа у форматі png |
saveButton_Click |
Реалізовано |
|
12 |
Виведення повідомлення про двудольність та еквівалентність графа |
equivalence_button_Click |
Реалізовано |
Результати тестів
Тест 1 – Меню програми
Меню програми представлено на рисунку 7.1

Рисунок 7.1 – Меню програми
Тест 2 – Створення вершин
Натискаємо кнопку створення вершин та рисуємо вершини на полотні.
Створенні вершини представлено на рисунку 7.2
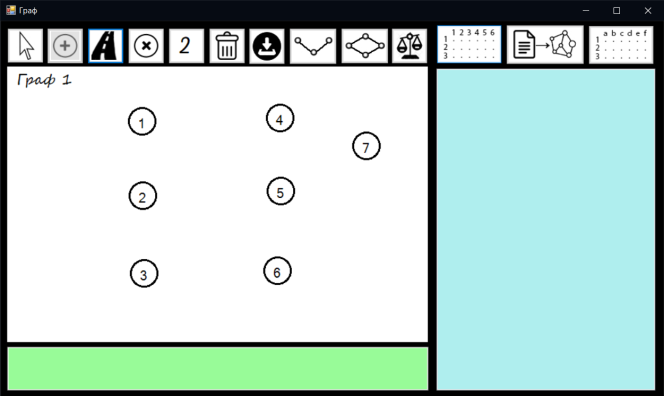
Рисунок 7.2 – Створення вершин
Тест 3 – Створення ребер
Натискаємо кнопку створити ребро та з’єднуємо дві вершини, натиснувши спочатку на одну а потім на іншу.
Створенні ребра представлено на рисунку 7.3
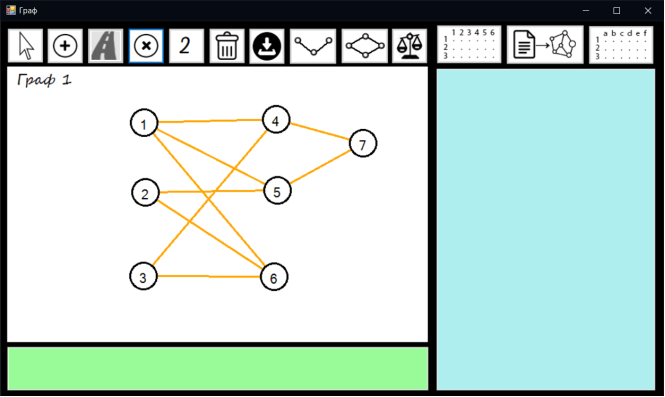
Рисунок 7.3 – Створення ребер
Тест 4 – Видалення вершин
Натискаємо на кнопку видалення вершин та натискаємо на вершину яку потрібно видалити.
Видалення вершин представлено на рисунку 7.4
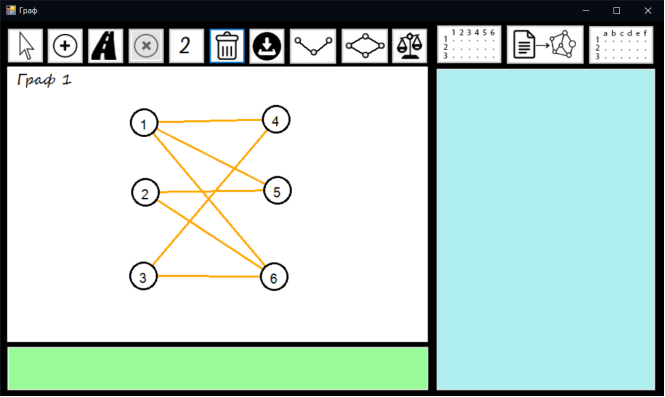
Рисунок 7.4 – Видалення вершин
Тест 5 – Видалення ребер
Натискаємо на кнопку видалення ребер та натискаємо на ребро яке потрібно видалити.
Видалення ребер представлено на рисунку 7.5
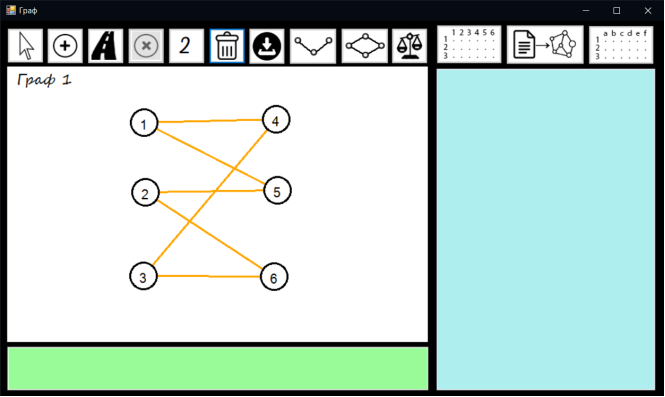
Рисунок 7.5 – Видалення ребер
Тест 6 – Переключення на другий граф
Натискаємо на кнопку переключення графа та рисуємо другий граф.
Переключення на другий граф представлено на рисунку 7.6
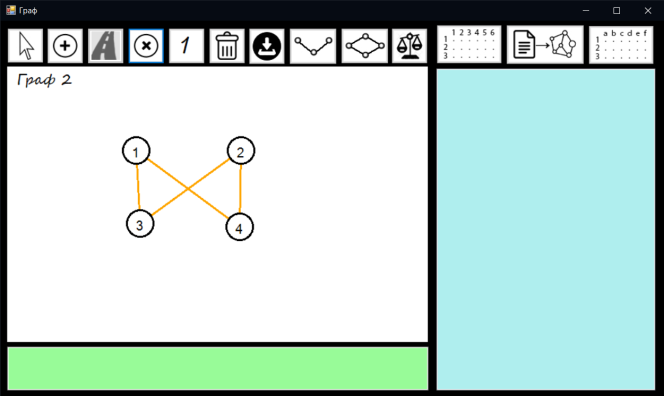
Рисунок 7.6 – Переключення на другий граф
Тест 7 – Зберегти граф
Натискаємо кнопку зберегти граф. Вибираємо формат та місце збереження.
Меню збереження графа представлено на рисунку 7.7
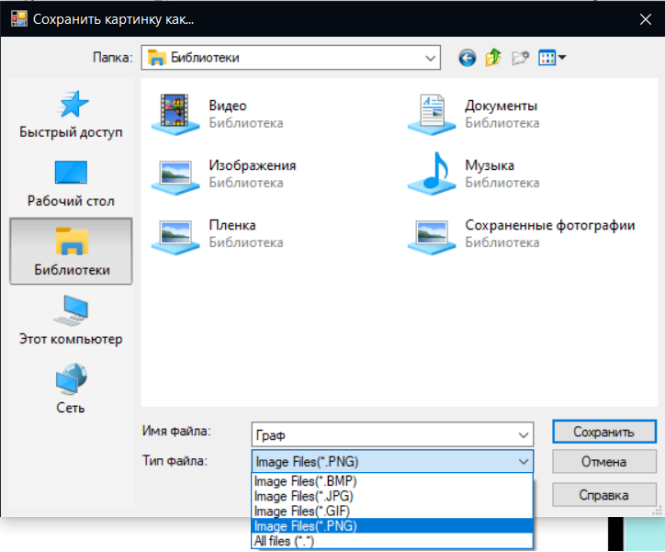
Рисунок 7.7 – Збереження графа
Тест 8 – Кнопка курсору
Натискаємо кнопку курсору та обираємо вершину. В listBoxMatrix виводиться ступінь обраної вершини.
Вивід ступеню вершини представлено на рисунку 7.8
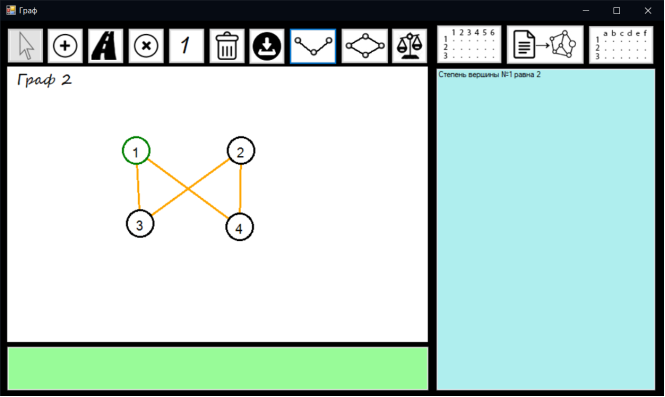
Рисунок 7.8 – Ступінь вершини
Тест 9 – Елементарні ланцюги
Натискаємо кнопку елементарні ланцюги. В listBoxMatrix виводяться всі елементарні ланцюги для обраного графа.
Вивід елементарних ланцюгів представлено на рисунку 7.9
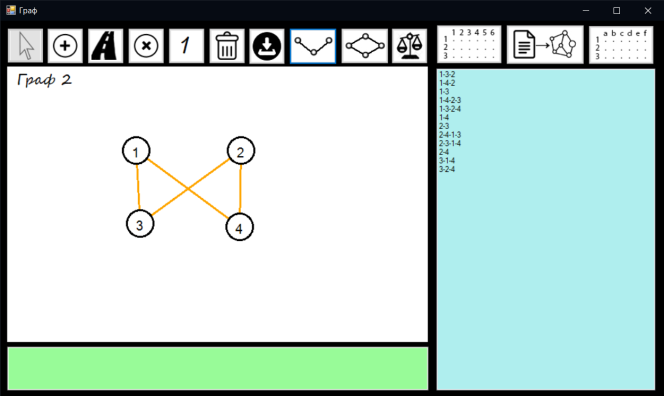
Рисунок 7.9 – Елементарні ланцюги
Тест 10 – Елементарні цикли
Натискаємо кнопку елементарні цикли. В listBoxMatrix виводяться всі елементарні цикли для обраного графа.
Вивід елементарних циклів представлено на рисунку 7.10
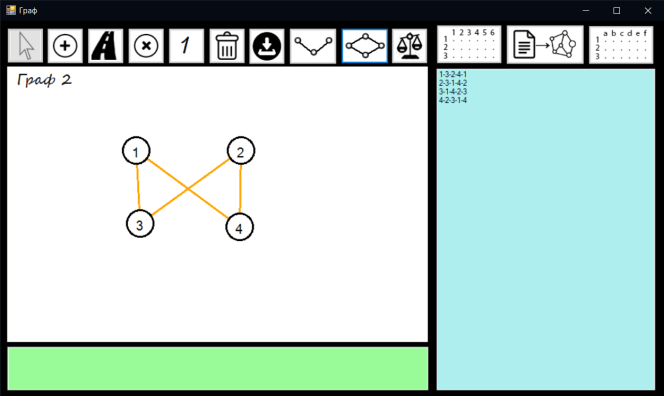
Рисунок 7.10 – Елементарні цикли
Тест 11 – Перевірка графів на двудольність та еквівалентність
Натискаємо кнопку порівняти графи. В Result виводиться результат двудольності графів та результат еквівалентності графів
Порівняння графів представлено на рисунку 7.11
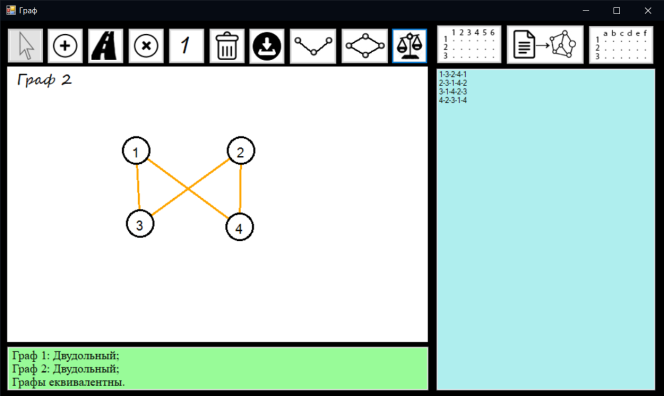
Рисунок 7.11 – Порівняння графів
Тест 12 – Матриця суміжності
Натискаємо кнопку матриця суміжності. В listBoxMatrix виводиться матриця суміжності для обраного графа.
Матриця суміжності представлено на рисунку 7.12
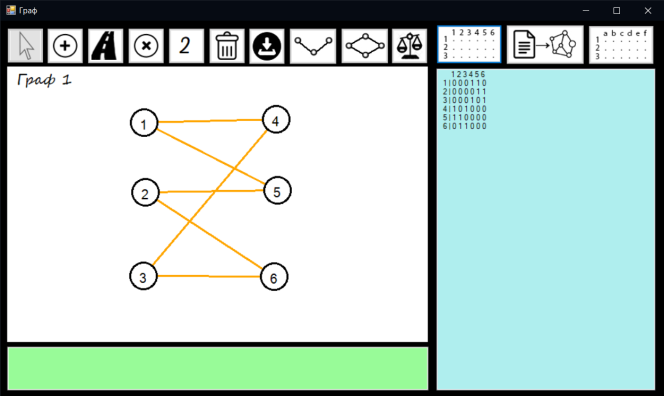
Рисунок 7.12 – Матриця суміжності
Тест 13 – Матриця інцидентності
Натискаємо кнопку матриця інцидентності. В listBoxMatrix виводиться матриця інцидентності для обраного графа.
Матрицю інцидентності представлено на рисунку 7.13
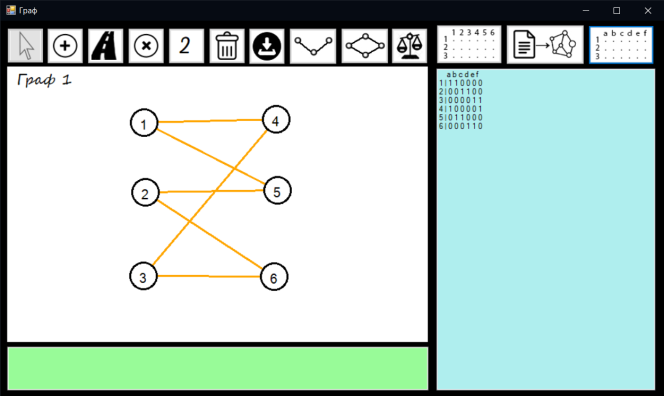
Рисунок 7.13 – Матриця інцидентності
Тест 14 – Видалення графа
Натискаємо на кнопку видалення графа. Відкривається попередження про видалення графа.
Попередження про видалення графа представлено на рисунку 7.14
Рисунок 7.14 – Попередження про видалення графа
Тест 15 – Загрузка графа з текстового документу
Натискаємо кнопку загрузити граф з текстового документу. Обираємо текстовий документ. Графи створюються.
Текстовий документ представлено на рисунку 7.15
Перший граф представлено на рисунку 7.16
Другий граф представлено на рисунку 7.17
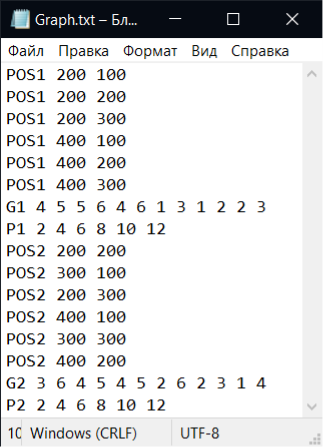
Рисунок 8.15 – Текстовий документ
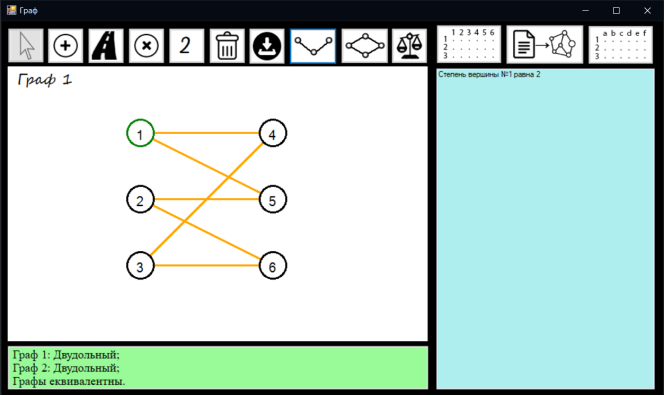
Рисунок 7.16 – Граф 1
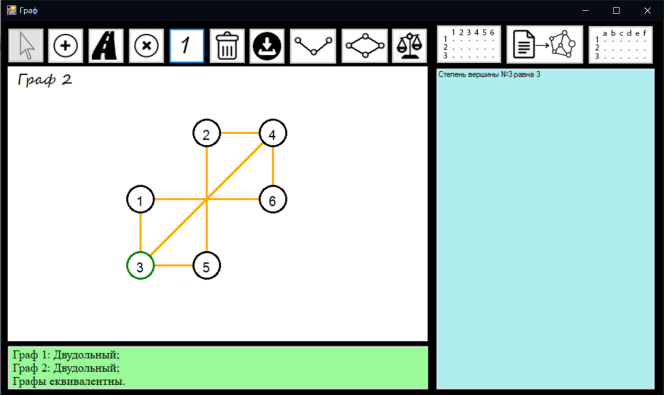
Рисунок 7.17 – Граф 2
На основі програми були створені юніт-тести Bipartite_GraphTests.
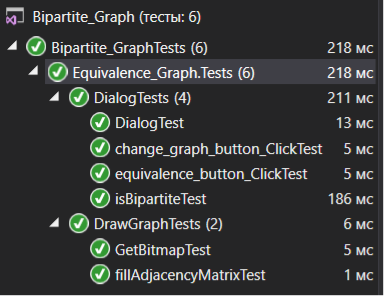
Рисунок 7.18 – Результати юніт-тестів
8. Висновки
Був розроблений додаток за допомогою якого можна працювати з неорієнтованими графами. Цей додаток допоможе в вивченні «Теорії графів».
Завдання, які було виконано:
- Побудова вершин та ребер графа (вершин не більше 20, ребер не більше 50);
- Виведення матриць сміжності та інцидентності;
- Зчитання графа з текстового файлу у форматі MFO;
- Видалення ребер та вершин графа;
- Зберігання графа;
- Визначення ступені вершин графа;
- Виведення ланцюгів та циклів графа;
- Визначення чи являється граф біхроматичним (двудольним);
- Створення Юніт-тестів.
У програми є недоліки, які з часом можна виправити:
- Графи можуть бути тільки неорієнтовані;
- Кількість вершин та ребер обмежена;
- Доречно було б зробити, щоб програма, перефарбовувала вершини при визначенні біхроматичності (двудольності) графа;
- Можна зробити необмежену кількість побудови графів (можна створити тільки 2 графа);
9. Знання та навички, отримані при проходженні практики
Під час проходження практики були отримані наступні навички:
- Проведення порівняльного аналізу мого додатку та вже існуючого.
- Розроблення UML-діаграм.
- Формулювання критерій прийняття (Acceptance Criteria).
- Формулювання актуальності теми, мета, об’єкт та предмет досліження.
- Розроблення тест-кейсів для верифікації продукту.
- Формулювання основних вимог до продукту (бізнес-вимоги, користувацькі вимоги, функціональні та нефункціональні вимоги).
Додаток А
НАСТАНОВА ОПЕРАТОРУ
- Призначення програми
Програма призначена для побудови графа, знаходження елементарних ланцюгів та циклів графа, знаходження матриць суміжності та інцидентності графа та перевірка графів на двудольність та еквівалентність.
- Технічні засоби для запуску програми
Для нормального функціонування даного програмного забезпечення потрібні такі мінімальні системні вимоги:
а) процесор з частотою не менше 2GHz;
б) оперативна пам'ять не менше 500MB;
в) місце на диску не менше 10MB;
г) дисплей і відеоадаптер будь-якого типу;
ґ) комп'ютерна миша;
д) клавіатура;
е) операційна система windows 7 і вище.
- Завантаження та робота з даною програмою
Для роботи з даною програмою потрібно запустити файл з розширенням .exe. Інсталяція даної програми не потрібна. Після запуску .exe файлу відкривається головне меню програми, що представлено на рисунку A.1

Рисунок A.1
В головному меню є кнопки для створення графа та для виводу інформації про граф. Також є полотно на якому буде відображатись граф та 2 поля для виводу інформації про граф. Опис всіх кнопок представлений в таблиці A.1.
Таблиця A.1 Опис кнопок головного меню
|
|
Визначає ступінь вершини графа |
|
|
Створює вершину графа |
|
|
Створює ребро графа |
|
|
Видаляє вершину або ребро графа |
Продовження таблиці A.1
|
|
Переключення між графами 1 та 2 |
|
|
Повністю видаляє граф |
|
|
Зберігає граф |
|
|
Виводить елементарні ланцюги |
|
|
Виводить елементарні цикли |
|
|
Визначає двудольність графів та зрівнює графи на еквівалентність |
|
|
Виводить матрицю суміжності |
|
|
Виводить матрицю інцидентності |
|
|
Створює граф з текстового документу |
Додаток Б
ВИХІДНИЙ ТЕКСТ ПРОГРАМИ
Graph.cs
using System;
using System.Collections.Generic;
using System.Windows.Forms;
using System.IO;
namespace Equivalence_Graph
{
public partial class Graph : Form
{
public bool graph = true;
public List<int> color_1;
public DrawGraph rendering_1;
public List<Vertex> vertexes_1;
public List<Edge> edges_1;
public List<int> color_2;
public DrawGraph rendering_2;
public List<Vertex> vertexes_2;
public List<Edge> edges_2;
public int[,] AdjacencyMatrix;
public int[,] IncidenceMatrix;
public int selected_1;
public int selected_2;
public Graph()
{
InitializeComponent();
vertexes_1 = new List<Vertex>();
rendering_1 = new DrawGraph(sheet.Width, sheet.Height);
edges_1 = new List<Edge>();
color_1 = new List<int>();
color_2 = new List<int>();
rendering_2 = new DrawGraph(sheet.Width, sheet.Height);
vertexes_2 = new List<Vertex>();
edges_2 = new List<Edge>();
sheet.Image = rendering_1.GetBitmap();
}
public void selectVertexButton_Click(object sender, EventArgs e)
{
mouse_button.Enabled = false;
add_vertex_button.Enabled = true;
add_edge_button.Enabled = true;
delete_vertex_button.Enabled = true;
if (graph)
{
rendering_1.clearSheet();
rendering_1.drawALLGraph(vertexes_1, edges_1);
sheet.Image = rendering_1.GetBitmap();
}
else
{
rendering_2.clearSheet();
rendering_2.drawALLGraph(vertexes_2, edges_2);
sheet.Image = rendering_2.GetBitmap();
}
selected_1 = -1;
}
public void drawVertexButton_Click(object sender, EventArgs e)
{
add_vertex_button.Enabled = false;
mouse_button.Enabled = true;
add_edge_button.Enabled = true;
delete_vertex_button.Enabled = true;
if (graph)
{
rendering_1.clearSheet();
rendering_1.drawALLGraph(vertexes_1, edges_1);
sheet.Image = rendering_1.GetBitmap();
}
else
{
rendering_2.clearSheet();
rendering_2.drawALLGraph(vertexes_2, edges_2);
sheet.Image = rendering_2.GetBitmap();
}
}
public void drawEdgeButton_Click(object sender, EventArgs e)
{
add_edge_button.Enabled = false;
mouse_button.Enabled = true;
add_vertex_button.Enabled = true;
delete_vertex_button.Enabled = true;
if (graph)
{
rendering_1.clearSheet();
rendering_1.drawALLGraph(vertexes_1, edges_1);
sheet.Image = rendering_1.GetBitmap();
}
else
{
rendering_2.clearSheet();
rendering_2.drawALLGraph(vertexes_2, edges_2);
sheet.Image = rendering_2.GetBitmap();
}
selected_1 = -1;
selected_2 = -1;
}
public void deleteButton_Click(object sender, EventArgs e)
{
delete_vertex_button.Enabled = false;
mouse_button.Enabled = true;
add_vertex_button.Enabled = true;
add_edge_button.Enabled = true;
if (graph)
{
rendering_1.clearSheet();
rendering_1.drawALLGraph(vertexes_1, edges_1);
sheet.Image = rendering_1.GetBitmap();
}
else
{
rendering_2.clearSheet();
rendering_2.drawALLGraph(vertexes_2, edges_2);
sheet.Image = rendering_2.GetBitmap();
}
}
public void deleteGraphButton_Click(object sender, EventArgs e)
{
mouse_button.Enabled = true;
add_vertex_button.Enabled = true;
add_edge_button.Enabled = true;
delete_vertex_button.Enabled = true;
const string message = "Вы действительно хотите полностью удалить граф?";
const string caption = "Удаление";
var MBSave = MessageBox.Show(message, caption, MessageBoxButtons.YesNo, MessageBoxIcon.Question);
if (MBSave == DialogResult.Yes)
{
if (graph)
{
color_1.Clear();
vertexes_1.Clear();
edges_1.Clear();
rendering_1.clearSheet();
sheet.Image = rendering_1.GetBitmap();
}
else
{
color_2.Clear();
vertexes_2.Clear();
edges_2.Clear();
rendering_2.clearSheet();
sheet.Image = rendering_2.GetBitmap();
}
}
}
public void adjacencyButton_Click(object sender, EventArgs e)
{
outputsAdjacency(graph);
}
public void incidenceButton_Click(object sender, EventArgs e)
{
createIncAndOut(graph);
}
public void sheet_MouseClick(object sender, MouseEventArgs e)
{
if (mouse_button.Enabled == false)
{
if (graph)
{
for (int i = 0; i < vertexes_1.Count; i++)
{
if (Math.Pow((vertexes_1[i].x - e.X), 2) + Math.Pow((vertexes_1[i].y - e.Y), 2) <= rendering_1.R * rendering_1.R)
{
if (selected_1 != -1)
{
selected_1 = -1;
rendering_1.clearSheet();
rendering_1.drawALLGraph(vertexes_1, edges_1);
sheet.Image = rendering_1.GetBitmap();
}
if (selected_1 == -1)
{
rendering_1.drawSelectedVertex(vertexes_1[i].x, vertexes_1[i].y);
selected_1 = i;
sheet.Image = rendering_1.GetBitmap();
outputsAdjacency(graph);
listBoxMatrix.Items.Clear();
int degree = 0;
for (int j = 0; j < vertexes_1.Count; j++)
degree += AdjacencyMatrix[selected_1, j];
listBoxMatrix.Items.Add("Степень вершины №" + (selected_1 + 1) + " равна " + degree);
break;
}
}
}
}
else
{
for (int i = 0; i < vertexes_2.Count; i++)
{
if (Math.Pow((vertexes_2[i].x - e.X), 2) + Math.Pow((vertexes_2[i].y - e.Y), 2) <= rendering_2.R * rendering_2.R)
{
if (selected_1 != -1)
{
selected_1 = -1;
rendering_2.clearSheet();
rendering_2.drawALLGraph(vertexes_2, edges_2);
sheet.Image = rendering_2.GetBitmap();
}
if (selected_1 == -1)
{
rendering_2.drawSelectedVertex(vertexes_2[i].x, vertexes_2[i].y);
selected_1 = i;
sheet.Image = rendering_2.GetBitmap();
outputsAdjacency(graph);
listBoxMatrix.Items.Clear();
int degree = 0;
for (int j = 0; j < vertexes_2.Count; j++)
degree += AdjacencyMatrix[selected_1, j];
listBoxMatrix.Items.Add("Степень вершины №" + (selected_1 + 1) + " равна " + degree);
break;
}
}
}
}
}
if (add_vertex_button.Enabled == false)
{
if (graph)
{
if(vertexes_1.Count < 20)
{
color_1.Add(-1);
vertexes_1.Add(new Vertex(e.X, e.Y));
rendering_1.drawVertex(e.X, e.Y, vertexes_1.Count.ToString());
sheet.Image = rendering_1.GetBitmap();
}
}
else
{
if (vertexes_2.Count < 20)
{
color_2.Add(-1);
vertexes_2.Add(new Vertex(e.X, e.Y));
rendering_2.drawVertex(e.X, e.Y, vertexes_1.Count.ToString());
sheet.Image = rendering_2.GetBitmap();
}
}
}
if (add_edge_button.Enabled == false)
{
if (graph)
{
if (edges_1.Count < 50)
{
if (e.Button == MouseButtons.Left)
{
for (int i = 0; i < vertexes_1.Count; i++)
{
if (Math.Pow((vertexes_1[i].x - e.X), 2) + Math.Pow((vertexes_1[i].y - e.Y), 2) <= rendering_1.R * rendering_1.R)
{
if (selected_1 == -1)
{
rendering_1.drawSelectedVertex(vertexes_1[i].x, vertexes_1[i].y);
selected_1 = i;
sheet.Image = rendering_1.GetBitmap();
break;
}
if (selected_2 == -1)
{
rendering_1.drawSelectedVertex(vertexes_1[i].x, vertexes_1[i].y);
selected_2 = i;
edges_1.Add(new Edge(selected_1, selected_2));
rendering_1.drawEdge(vertexes_1[selected_1], vertexes_1[selected_2], edges_1[edges_1.Count - 1], edges_1.Count - 1);
selected_1 = -1;
selected_2 = -1;
sheet.Image = rendering_1.GetBitmap();
break;
}
}
}
}
if (e.Button == MouseButtons.Right)
{
if ((selected_1 != -1) &&
(Math.Pow((vertexes_1[selected_1].x - e.X), 2) + Math.Pow((vertexes_1[selected_1].y - e.Y), 2) <= rendering_1.R * rendering_1.R))
{
rendering_1.drawVertex(vertexes_1[selected_1].x, vertexes_1[selected_1].y, (selected_1 + 1).ToString());
selected_1 = -1;
sheet.Image = rendering_1.GetBitmap();
}
}
}
}
else
{
if (edges_2.Count < 50)
{
if (e.Button == MouseButtons.Left)
{
for (int i = 0; i < vertexes_2.Count; i++)
{
if (Math.Pow((vertexes_2[i].x - e.X), 2) + Math.Pow((vertexes_2[i].y - e.Y), 2) <= rendering_2.R * rendering_2.R)
{
if (selected_1 == -1)
{
rendering_2.drawSelectedVertex(vertexes_2[i].x, vertexes_2[i].y);
selected_1 = i;
sheet.Image = rendering_2.GetBitmap();
break;
}
if (selected_2 == -1)
{
rendering_2.drawSelectedVertex(vertexes_2[i].x, vertexes_2[i].y);
selected_2 = i;
edges_2.Add(new Edge(selected_1, selected_2));
rendering_2.drawEdge(vertexes_2[selected_1], vertexes_2[selected_2], edges_2[edges_2.Count - 1], edges_2.Count - 1);
selected_1 = -1;
selected_2 = -1;
sheet.Image = rendering_2.GetBitmap();
break;
}
}
}
}
if (e.Button == MouseButtons.Right)
{
if ((selected_1 != -1) &&
(Math.Pow((vertexes_2[selected_1].x - e.X), 2) + Math.Pow((vertexes_2[selected_1].y - e.Y), 2) <= rendering_2.R * rendering_2.R))
{
rendering_2.drawVertex(vertexes_2[selected_1].x, vertexes_2[selected_1].y, (selected_1 + 1).ToString());
selected_1 = -1;
sheet.Image = rendering_2.GetBitmap();
}
}
}
}
}
if (delete_vertex_button.Enabled == false)
{
if (graph)
{
bool flag = false;
for (int i = 0; i < vertexes_1.Count; i++)
{
if (Math.Pow((vertexes_1[i].x - e.X), 2) + Math.Pow((vertexes_1[i].y - e.Y), 2) <= rendering_1.R * rendering_1.R)
{
for (int j = 0; j < edges_1.Count; j++)
{
if ((edges_1[j].v1 == i) || (edges_1[j].v2 == i))
{
edges_1.RemoveAt(j);
j--;
}
else
{
if (edges_1[j].v1 > i) edges_1[j].v1--;
if (edges_1[j].v2 > i) edges_1[j].v2--;
}
}
vertexes_1.RemoveAt(i);
flag = true;
break;
}
}
if (!flag)
{
for (int i = 0; i < edges_1.Count; i++)
{
if (edges_1[i].v1 == edges_1[i].v2)
{
if ((Math.Pow((vertexes_1[edges_1[i].v1].x - rendering_1.R - e.X), 2) + Math.Pow((vertexes_1[edges_1[i].v1].y - rendering_1.R - e.Y), 2) <= ((rendering_1.R + 2) * (rendering_1.R + 2))) &&
(Math.Pow((vertexes_1[edges_1[i].v1].x - rendering_1.R - e.X), 2) + Math.Pow((vertexes_1[edges_1[i].v1].y - rendering_1.R - e.Y), 2) >= ((rendering_1.R - 2) * (rendering_1.R - 2))))
{
edges_1.RemoveAt(i);
flag = true;
break;
}
}
else
{
if (((e.X - vertexes_1[edges_1[i].v1].x) * (vertexes_1[edges_1[i].v2].y - vertexes_1[edges_1[i].v1].y) / (vertexes_1[edges_1[i].v2].x - vertexes_1[edges_1[i].v1].x) + vertexes_1[edges_1[i].v1].y) <= (e.Y + 4) &&
((e.X - vertexes_1[edges_1[i].v1].x) * (vertexes_1[edges_1[i].v2].y - vertexes_1[edges_1[i].v1].y) / (vertexes_1[edges_1[i].v2].x - vertexes_1[edges_1[i].v1].x) + vertexes_1[edges_1[i].v1].y) >= (e.Y - 4))
{
if ((vertexes_1[edges_1[i].v1].x <= vertexes_1[edges_1[i].v2].x && vertexes_1[edges_1[i].v1].x <= e.X && e.X <= vertexes_1[edges_1[i].v2].x) ||
(vertexes_1[edges_1[i].v1].x >= vertexes_1[edges_1[i].v2].x && vertexes_1[edges_1[i].v1].x >= e.X && e.X >= vertexes_1[edges_1[i].v2].x))
{
edges_1.RemoveAt(i);
flag = true;
break;
}
}
}
}
}
if (flag)
{
rendering_1.clearSheet();
if (graph)
{
rendering_1.drawALLGraph(vertexes_1, edges_1);
}
else
{
rendering_1.drawALLGraph(vertexes_2, edges_2);
}
sheet.Image = rendering_1.GetBitmap();
}
}
else
{
bool flag = false;
for (int i = 0; i < vertexes_2.Count; i++)
{
if (Math.Pow((vertexes_2[i].x - e.X), 2) + Math.Pow((vertexes_2[i].y - e.Y), 2) <= rendering_2.R * rendering_2.R)
{
for (int j = 0; j < edges_2.Count; j++)
{
if ((edges_2[j].v1 == i) || (edges_2[j].v2 == i))
{
edges_2.RemoveAt(j);
j--;
}
else
{
if (edges_2[j].v1 > i) edges_2[j].v1--;
if (edges_2[j].v2 > i) edges_2[j].v2--;
}
}
vertexes_2.RemoveAt(i);
flag = true;
break;
}
}
if (!flag)
{
for (int i = 0; i < edges_1.Count; i++)
{
if (edges_1[i].v1 == edges_1[i].v2)
{
if ((Math.Pow((vertexes_2[edges_1[i].v1].x - rendering_2.R - e.X), 2) + Math.Pow((vertexes_2[edges_1[i].v1].y - rendering_2.R - e.Y), 2) <= ((rendering_2.R + 2) * (rendering_2.R + 2))) &&
(Math.Pow((vertexes_2[edges_1[i].v1].x - rendering_2.R - e.X), 2) + Math.Pow((vertexes_2[edges_1[i].v1].y - rendering_2.R - e.Y), 2) >= ((rendering_2.R - 2) * (rendering_2.R - 2))))
{
edges_2.RemoveAt(i);
flag = true;
break;
}
}
else
{
if (((e.X - vertexes_2[edges_1[i].v1].x) * (vertexes_2[edges_1[i].v2].y - vertexes_2[edges_1[i].v1].y) / (vertexes_2[edges_1[i].v2].x - vertexes_2[edges_1[i].v1].x) + vertexes_2[edges_1[i].v1].y) <= (e.Y + 4) &&
((e.X - vertexes_2[edges_1[i].v1].x) * (vertexes_2[edges_1[i].v2].y - vertexes_2[edges_1[i].v1].y) / (vertexes_2[edges_1[i].v2].x - vertexes_2[edges_1[i].v1].x) + vertexes_2[edges_1[i].v1].y) >= (e.Y - 4))
{
if ((vertexes_2[edges_1[i].v1].x <= vertexes_2[edges_1[i].v2].x && vertexes_2[edges_1[i].v1].x <= e.X && e.X <= vertexes_2[edges_1[i].v2].x) ||
(vertexes_2[edges_1[i].v1].x >= vertexes_2[edges_1[i].v2].x && vertexes_2[edges_1[i].v1].x >= e.X && e.X >= vertexes_2[edges_1[i].v2].x))
{
edges_2.RemoveAt(i);
flag = true;
break;
}
}
}
}
}
if (flag)
{
rendering_2.clearSheet();
if (graph)
{
rendering_2.drawALLGraph(vertexes_1, edges_1);
}
else
{
rendering_2.drawALLGraph(vertexes_2, edges_2);
}
sheet.Image = rendering_2.GetBitmap();
}
}
}
}
public void outputsAdjacency(bool m_graph)
{
if (m_graph)
{
AdjacencyMatrix = new int[vertexes_1.Count, vertexes_1.Count];
rendering_1.fillAdjacencyMatrix(vertexes_1.Count, edges_1, AdjacencyMatrix);
listBoxMatrix.Items.Clear();
string sOut = " ";
for (int i = 0; i < vertexes_1.Count; i++)
sOut += (i + 1) + " ";
listBoxMatrix.Items.Add(sOut);
for (int i = 0; i < vertexes_1.Count; i++)
{
if (i < 9) {
sOut = " " + (i + 1) + " | ";
}
else
{
sOut = (i + 1) + " | ";
}
for (int j = 0; j < vertexes_1.Count; j++)
{
sOut += AdjacencyMatrix[i, j] + " ";
if (j >= 9) {
sOut += " ";
}
}
listBoxMatrix.Items.Add(sOut);
}
}
else
{
AdjacencyMatrix = new int[vertexes_2.Count, vertexes_2.Count];
rendering_2.fillAdjacencyMatrix(vertexes_2.Count, edges_2, AdjacencyMatrix);
listBoxMatrix.Items.Clear();
string sOut = " ";
for (int i = 0; i < vertexes_2.Count; i++)
sOut += (i + 1) + " ";
listBoxMatrix.Items.Add(sOut);
for (int i = 0; i < vertexes_2.Count; i++)
{
if (i < 9)
{
sOut = " " + (i + 1) + " | ";
}
else
{
sOut = (i + 1) + " | ";
}
for (int j = 0; j < vertexes_2.Count; j++)
{
sOut += AdjacencyMatrix[i, j] + " ";
if (j >= 9)
{
sOut += " ";
}
}
listBoxMatrix.Items.Add(sOut);
}
}
}
public void createIncAndOut(bool m_graph)
{
if (m_graph)
{
if (edges_1.Count > 0)
{
IncidenceMatrix = new int[vertexes_1.Count, edges_1.Count];
rendering_1.fillIncidenceMatrix(vertexes_1.Count, edges_1, IncidenceMatrix);
listBoxMatrix.Items.Clear();
string sOut = " ";
for (int i = 0; i < edges_1.Count; i++)
sOut += (char)('a' + i) + " ";
listBoxMatrix.Items.Add(sOut);
for (int i = 0; i < vertexes_1.Count; i++)
{
sOut = (i + 1) + " | ";
for (int j = 0; j < edges_1.Count; j++)
sOut += IncidenceMatrix[i, j] + " ";
listBoxMatrix.Items.Add(sOut);
}
}
else
listBoxMatrix.Items.Clear();
}
else
{
if (edges_2.Count > 0)
{
IncidenceMatrix = new int[vertexes_2.Count, edges_2.Count];
rendering_2.fillIncidenceMatrix(vertexes_2.Count, edges_2, IncidenceMatrix);
listBoxMatrix.Items.Clear();
string sOut = " ";
for (int i = 0; i < edges_2.Count; i++)
sOut += (char)('a' + i) + " ";
listBoxMatrix.Items.Add(sOut);
for (int i = 0; i < vertexes_2.Count; i++)
{
sOut = (i + 1) + " | ";
for (int j = 0; j < edges_2.Count; j++)
sOut += IncidenceMatrix[i, j] + " ";
listBoxMatrix.Items.Add(sOut);
}
}
else
listBoxMatrix.Items.Clear();
}
}
public void chainButton_Click(object sender, EventArgs e)
{
if (graph)
{
listBoxMatrix.Items.Clear();
int[] color = new int[vertexes_1.Count];
for (int i = 0; i < vertexes_1.Count - 1; i++)
for (int j = i + 1; j < vertexes_1.Count; j++)
{
for (int k = 0; k < vertexes_1.Count; k++)
color[k] = 1;
DFSchain(i, j, edges_1, color, (i + 1).ToString());
}
}
else
{
listBoxMatrix.Items.Clear();
int[] color = new int[vertexes_2.Count];
for (int i = 0; i < vertexes_2.Count - 1; i++)
for (int j = i + 1; j < vertexes_2.Count; j++)
{
for (int k = 0; k < vertexes_2.Count; k++)
color[k] = 1;
DFSchain(i, j, edges_2, color, (i + 1).ToString());
}
}
}
public void DFSchain(int u, int endV, List<Edge> E, int[] color, string s)
{
if (u != endV)
color[u] = 2;
else
{
listBoxMatrix.Items.Add(s);
return;
}
for (int w = 0; w < E.Count; w++)
{
if (color[E[w].v2] == 1 && E[w].v1 == u)
{
DFSchain(E[w].v2, endV, E, color, s + "-" + (E[w].v2 + 1).ToString());
color[E[w].v2] = 1;
}
else if (color[E[w].v1] == 1 && E[w].v2 == u)
{
DFSchain(E[w].v1, endV, E, color, s + "-" + (E[w].v1 + 1).ToString());
color[E[w].v1] = 1;
}
}
}
public void cycleButton_Click(object sender, EventArgs e)
{
if (graph)
{
listBoxMatrix.Items.Clear();
int[] color = new int[vertexes_1.Count];
for (int i = 0; i < vertexes_1.Count; i++)
{
for (int k = 0; k < vertexes_1.Count; k++)
color[k] = 1;
List<int> cycle = new List<int>();
cycle.Add(i + 1);
DFScycle(i, i, edges_1, color, -1, cycle);
}
}
else
{
listBoxMatrix.Items.Clear();
int[] color = new int[vertexes_2.Count];
for (int i = 0; i < vertexes_2.Count; i++)
{
for (int k = 0; k < vertexes_2.Count; k++)
color[k] = 1;
List<int> cycle = new List<int>();
cycle.Add(i + 1);
DFScycle(i, i, edges_2, color, -1, cycle);
}
}
}
public void DFScycle(int u, int endV, List<Edge> E, int[] color, int unavailableEdge, List<int> cycle)
{
if (u != endV)
color[u] = 2;
else
{
if (cycle.Count >= 2)
{
cycle.Reverse();
string s = cycle[0].ToString();
for (int i = 1; i < cycle.Count; i++)
s += "-" + cycle[i].ToString();
bool flag = false;
for (int i = 0; i < listBoxMatrix.Items.Count; i++)
if (listBoxMatrix.Items[i].ToString() == s)
{
flag = true;
break;
}
if (!flag)
{
cycle.Reverse();
s = cycle[0].ToString();
for (int i = 1; i < cycle.Count; i++)
s += "-" + cycle[i].ToString();
listBoxMatrix.Items.Add(s);
}
return;
}
}
for (int w = 0; w < E.Count; w++)
{
if (w == unavailableEdge)
continue;
if (color[E[w].v2] == 1 && E[w].v1 == u)
{
List<int> cycleNEW = new List<int>(cycle);
cycleNEW.Add(E[w].v2 + 1);
DFScycle(E[w].v2, endV, E, color, w, cycleNEW);
color[E[w].v2] = 1;
}
else if (color[E[w].v1] == 1 && E[w].v2 == u)
{
List<int> cycleNEW = new List<int>(cycle);
cycleNEW.Add(E[w].v1 + 1);
DFScycle(E[w].v1, endV, E, color, w, cycleNEW);
color[E[w].v1] = 1;
}
}
}
public void saveButton_Click(object sender, EventArgs e)
{
if (sheet.Image != null)
{
SaveFileDialog savedialog = new SaveFileDialog();
savedialog.Title = "Сохранить картинку как...";
savedialog.OverwritePrompt = true;
savedialog.CheckPathExists = true;
savedialog.Filter = "Image Files(*.BMP)|*.BMP|Image Files(*.JPG)|*.JPG|Image Files(*.GIF)|*.GIF|Image Files(*.PNG)|*.PNG|All files (*.*)|*.*";
savedialog.ShowHelp = true;
if (savedialog.ShowDialog() == DialogResult.OK)
{
try
{
sheet.Image.Save(savedialog.FileName, System.Drawing.Imaging.ImageFormat.Jpeg);
}
catch
{
MessageBox.Show("Невозможно сохранить изображение", "Ошибка",
MessageBoxButtons.OK, MessageBoxIcon.Error);
}
}
}
}
public void change_graph_button_Click(object sender, EventArgs e)
{
graph = !graph;
rendering_1.clearSheet();
if (graph)
{
change_graph_button.Text = "2";
rendering_1.drawALLGraph(vertexes_1, edges_1);
Graph1.Visible = true;
Graph2.Visible = false;
}
else
{
change_graph_button.Text = "1";
rendering_1.drawALLGraph(vertexes_2, edges_2);
Graph2.Visible = true;
Graph1.Visible = false;
}
sheet.Image = rendering_1.GetBitmap();
}
public void addEdge(List<List<int>> adj, Edge i)
{
adj[i.v1].Add(i.v2);
adj[i.v2].Add(i.v1);
}
public void equivalence_button_Click(object sender, EventArgs e)
{
List<List<int>> adj = new List<List<int>>(vertexes_1.Count + 1);
List<List<int>> adj_1 = new List<List<int>>(vertexes_1.Count + 1);
for (int i = 0; i <= vertexes_1.Count; i++)
{
adj.Add(new List<int>());
}
for (int i = 0; i <= vertexes_2.Count; i++)
{
adj_1.Add(new List<int>());
}
for (int i = 0; i < color_1.Count; i++)
{
color_1[i] = -1;
}
for (int i = 0; i < color_2.Count; i++)
{
color_2[i] = -1;
}
color_1[1] = 0;
color_2[1] = 0;
bool[] visited = new bool[vertexes_1.Count + 1];
bool[] visited_1 = new bool[vertexes_2.Count + 1];
visited[1] = true;
visited_1[1] = true;
foreach (Edge i in edges_1)
{
addEdge(adj, i);
}
foreach (Edge i in edges_2)
{
addEdge(adj_1, i);
}
bool graph_1 = isBipartite(adj, 1, visited, color_1);
bool graph_2 = isBipartite(adj_1, 1, visited_1, color_2);
if (graph_1 && graph_2)
{
Result.Text = "Граф 1: Двудольный;\r\nГраф 2: Двудольный;\r\n";
}
else if (graph_1 && !graph_2)
{
Result.Text = "Граф 1: Двудольный;\r\nГраф 2: Не двудольный;\r\n";
}
else if (!graph_1 && graph_2)
{
Result.Text = "Граф 1: Не двудольный;\r\nГраф 2: Двудольный;\r\n";
}
else if (!graph_1 && !graph_2)
{
Result.Text = "Граф 1: Не двудольный;\r\nГраф 2: Не двудольный;\r\n";
}
if (isBipartite(adj, 1, visited, color_1) == isBipartite(adj_1, 1, visited_1, color_2))
{
Result.Text += "Графы еквивалентны.";
}
else
{
Result.Text += "Графы не еквивалентны.";
}
}
public string get_result()
{
return Result.Text;
}
public bool isBipartite(List<List<int>> adj, int v, bool[] visited, List<int> color)
{
foreach (int u in adj[v])
{
if (visited[u] == false)
{
visited[u] = true;
color[u] = 1 - color[v];
if (!isBipartite(adj, u, visited, color))
return false;
}
else if (color[u] == color[v])
return false;
}
return true;
}
public void read_file_button_Click(object sender, EventArgs e)
{
OpenFileDialog openFileDialog = new OpenFileDialog();
openFileDialog.Title = "Чтение графa...";
openFileDialog.CheckPathExists = true;
openFileDialog.Filter = "Text Files(*.TXT)|*.txt|All files (*.*)|*.*";
openFileDialog.ShowHelp = true;
if (openFileDialog.ShowDialog() == DialogResult.OK)
{
using (StreamReader reader = new StreamReader(openFileDialog.FileName))
{
string line;
List<List<int>> position1 = new List<List<int>>();
List<List<int>> position2 = new List<List<int>>();
List<int> mass_g1 = new List<int>();
List<int> mass_p1 = new List<int>();
List<int> mass_g2 = new List<int>();
List<int> mass_p2 = new List<int>();
while ((line = reader.ReadLine()) != null)
{
List<int> temp = new List<int>();
List<string> s_temp = new List<string>(line.Split(' '));
switch (s_temp[0])
{
case "G1":
s_temp.RemoveAt(0);
foreach (string s in s_temp)
{
mass_g1.Add(int.Parse(s));
}
break;
case "G2":
s_temp.RemoveAt(0);
foreach (string s in s_temp)
{
mass_g2.Add(int.Parse(s));
}
break;
case "P1":
s_temp.RemoveAt(0);
foreach (string s in s_temp)
{
mass_p1.Add(int.Parse(s));
}
break;
case "P2":
s_temp.RemoveAt(0);
foreach (string s in s_temp)
{
mass_p2.Add(int.Parse(s));
}
break;
case "POS1":
s_temp.RemoveAt(0);
foreach (string s in s_temp)
{
temp.Add(int.Parse(s));
}
position1.Add(temp);
break;
case "POS2":
s_temp.RemoveAt(0);
foreach (string s in s_temp)
{
temp.Add(int.Parse(s));
}
position2.Add(temp);
break;
}
}
vertexes_1.Clear();
edges_1.Clear();
color_1.Clear();
rendering_1.clearSheet();
vertexes_2.Clear();
edges_2.Clear();
color_2.Clear();
rendering_2.clearSheet();
foreach (List<int> p1 in position1)
{
color_1.Add(-1);
vertexes_1.Add(new Vertex(p1[0], p1[1]));
}
foreach (List<int> p2 in position2)
{
color_2.Add(-1);
vertexes_2.Add(new Vertex(p2[0], p2[1]));
}
int i = 0;
int index = 0;
foreach (int p in mass_p1)
{
for (; i < p; i++)
{
edges_1.Add(new Edge(index, mass_g1[i] - 1));
}
index++;
}
i = 0;
index = 0;
foreach (int p in mass_p2)
{
for (; i < p; i++)
{
edges_2.Add(new Edge(index, mass_g2[i] - 1));
}
index++;
}
if (graph)
{
rendering_1.drawALLGraph(vertexes_1, edges_1);
sheet.Image = rendering_1.GetBitmap();
}
else
{
rendering_2.drawALLGraph(vertexes_2, edges_2);
sheet.Image = rendering_2.GetBitmap();
}
}
}
}
}
}
DrawGraph.cs
using System.Collections.Generic;
using System.Drawing;
namespace Equivalence_Graph
{
public class Vertex
{
public int x, y;
public Vertex(int x, int y)
{
this.x = x;
this.y = y;
}
}
public class Edge
{
public int v1, v2;
public Edge(int v1, int v2)
{
this.v1 = v1;
this.v2 = v2;
}
}
public class DrawGraph
{
Bitmap bitmap;
Pen blackPen;
Pen greenPen;
Pen orangePen;
Graphics gr;
Font fo;
Brush br;
PointF point;
public int R = 20;
public DrawGraph(int width, int height)
{
bitmap = new Bitmap(width, height);
gr = Graphics.FromImage(bitmap);
clearSheet();
blackPen = new Pen(Color.Black);
blackPen.Width = 3;
greenPen = new Pen(Color.Green);
greenPen.Width = 3;
orangePen = new Pen(Color.Orange);
orangePen.Width = 3;
fo = new Font("Nexa Script", 15);
br = Brushes.Black;
}
public Bitmap GetBitmap()
{
return bitmap;
}
public void clearSheet()
{
gr.Clear(Color.White);
}
public void drawVertex(int x, int y, string number)
{
gr.FillEllipse(Brushes.White, (x - R), (y - R), 2 * R, 2 * R);
gr.DrawEllipse(blackPen, (x - R), (y - R), 2 * R, 2 * R);
point = new PointF(x - 9, y - 9);
gr.DrawString(number, fo, br, point);
}
public void drawSelectedVertex(int x, int y)
{
gr.DrawEllipse(greenPen, (x - R), (y - R), 2 * R, 2 * R);
}
public void drawEdge(Vertex V1, Vertex V2, Edge E, int numberE)
{
if (E.v1 == E.v2)
{
gr.DrawArc(orangePen, (V1.x - 2 * R), (V1.y - 2 * R), 2 * R, 2 * R, 90, 270);
point = new PointF(V1.x - (int)(2.75 * R), V1.y - (int)(2.75 * R));
drawVertex(V1.x, V1.y, (E.v1 + 1).ToString());
}
else
{
gr.DrawLine(orangePen, V1.x, V1.y, V2.x, V2.y);
point = new PointF((V1.x + V2.x) / 2, (V1.y + V2.y) / 2);
drawVertex(V1.x, V1.y, (E.v1 + 1).ToString());
drawVertex(V2.x, V2.y, (E.v2 + 1).ToString());
}
}
public void drawALLGraph(List<Vertex> V, List<Edge> E)
{
for (int i = 0; i < E.Count; i++)
{
if (E[i].v1 == E[i].v2)
{
gr.DrawArc(orangePen, (V[E[i].v1].x - 2 * R), (V[E[i].v1].y - 2 * R), 2 * R, 2 * R, 90, 270);
point = new PointF(V[E[i].v1].x - (int)(2.75 * R), V[E[i].v1].y - (int)(2.75 * R));
}
else
{
gr.DrawLine(orangePen, V[E[i].v1].x, V[E[i].v1].y, V[E[i].v2].x, V[E[i].v2].y);
point = new PointF((V[E[i].v1].x + V[E[i].v2].x) / 2, (V[E[i].v1].y + V[E[i].v2].y) / 2);
}
}
for (int i = 0; i < V.Count; i++)
{
drawVertex(V[i].x, V[i].y, (i + 1).ToString());
}
}
public void fillAdjacencyMatrix(int numberV, List<Edge> E, int[,] matrix)
{
for (int i = 0; i < numberV; i++)
for (int j = 0; j < numberV; j++)
matrix[i, j] = 0;
for (int i = 0; i < E.Count; i++)
{
matrix[E[i].v1, E[i].v2] = 1;
matrix[E[i].v2, E[i].v1] = 1;
}
}
public void fillIncidenceMatrix(int numberV, List<Edge> E, int[,] matrix)
{
for (int i = 0; i < numberV; i++)
for (int j = 0; j < E.Count; j++)
matrix[i, j] = 0;
for (int i = 0; i < E.Count; i++)
{
matrix[E[i].v1, i] = 1;
matrix[E[i].v2, i] = 1;
}
}
}
}
Юніт-тести
DialogTests.cs
using Microsoft.VisualStudio.TestTools.UnitTesting;
using System.Collections.Generic;
using System.Windows.Forms;
namespace Equivalence_Graph.Tests {
[TestClass()]
public class DialogTests
{
Graph form = new Graph();
[TestMethod()]
public void isBipartiteTest()
{
List<Edge> E = new List<Edge>();
for (int i = 1; i <= 5; i++)
for (int x = 1; x <= 5; x++)
E.Add(new Edge(i, x));
int Count = 6;
List<List<int>> adj = new List<List<int>>(Count + 1);
for (int i = 0; i <= Count; i++)
{
adj.Add(new List<int>());
}
List<int> color_1 = new List<int>();
for (int i = 0; i < Count; i++)
{
color_1.Add(-1);
}
color_1[1] = 0;
bool[] visited = new bool[Count + 1];
visited[1] = true;
foreach (Edge i in E)
{
form.addEdge(adj, i);
}
bool graph_1 = form.isBipartite(adj, 1, visited, color_1);
Assert.AreEqual(false, graph_1);
}
[TestMethod()]
public void change_graph_button_ClickTest()
{
form.change_graph_button_Click(null, null);
Assert.AreEqual(form.graph, false);
form.change_graph_button_Click(null, null);
Assert.AreEqual(form.graph, true);
form.change_graph_button_Click(null, null);
Assert.AreEqual(form.graph, false);
form.change_graph_button_Click(null, null);
Assert.AreEqual(form.graph, true);
}
[TestMethod()]
public void equivalence_button_ClickTest()
{
List<Edge> E = new List<Edge>();
for (int i = 1; i <= 5; i++)
for (int x = 1; x <= 5; x++)
E.Add(new Edge(i, x));
List<Edge> E1 = new List<Edge>();
for (int i = 1; i <= 5; i++)
for (int x = 1; x <= 5; x++)
E1.Add(new Edge(i, x));
form.edges_1 = E;
form.edges_2 = E1;
//List<int> color_1 = new List<int>();
for (int i = 0; i < 6; i++)
{
form.color_1.Add(-1);
form.vertexes_1.Add(new Vertex(15, 15));
form.color_2.Add(-1);
form.vertexes_2.Add(new Vertex(15, 15));
}
form.equivalence_button_Click(null,null);
string str = "Граф 1: Не двудольный;\r\nГраф 2: Не двудольный;\r\nГрафы еквивалентны.";
string str2 = form.get_result();
Assert.AreEqual(str, str2);
}
[TestMethod()]
public void DialogTest()
{
form.drawVertexButton_Click(null, null);
form.sheet_MouseClick(null, new MouseEventArgs(new MouseButtons(), 0, 100, 100, 0));
form.sheet_MouseClick(null, new MouseEventArgs(new MouseButtons(), 0, 150, 150, 0));
List<Vertex> V = new List<Vertex>();
V.Add(new Vertex(100, 100));
V.Add(new Vertex(150, 150));
for(int i = 0; i < V.Count; i++) {
Assert.AreEqual(form.vertexes_1[i].x, V[i].x);
Assert.AreEqual(form.vertexes_1[i].y, V[i].y);
}
form.drawEdgeButton_Click(null, null);
form.sheet_MouseClick(null, new MouseEventArgs(new MouseButtons(), 0, 100, 100, 0));
form.sheet_MouseClick(null, new MouseEventArgs(new MouseButtons(), 0, 150, 150, 0));
List<Edge> edges_1;
edges_1 = form.edges_1;
for (int i = 0; i < edges_1.Count; i++)
{
Assert.AreEqual(edges_1[i].v1, 1);
Assert.AreEqual(edges_1[i].v1, 2);
}
form.deleteButton_Click(null, null);
form.sheet_MouseClick(null, new MouseEventArgs(new MouseButtons(), 0, 100, 100, 0));
form.sheet_MouseClick(null, new MouseEventArgs(new MouseButtons(), 0, 150, 150, 0));
V.Clear();
for (int i = 0; i < V.Count; i++) {
Assert.AreEqual(form.vertexes_1[i].x, V[i].x);
Assert.AreEqual(form.vertexes_1[i].y, V[i].y);
}
}
}
}
DrawGraphTests.cs
using Microsoft.VisualStudio.TestTools.UnitTesting;
using System.IO;
using System.Collections.Generic;
using System.Drawing;
namespace Equivalence_Graph.Tests
{
[TestClass()]
public class DrawGraphTests
{
DrawGraph drawgraph;
Graphics gr;
[TestMethod()]
public void fillAdjacencyMatrixTest()
{
drawgraph = new DrawGraph(500, 500);
int numberV2 = 6; List<Edge> E2 = new List<Edge>(); int[,] matrix2 = new int[6,6];
Edge e = new Edge(1, 1);
for (int i = 1; i <= 5; i++)
for (int x = 1; x <= 5; x++)
E2.Add(new Edge(i, x));
//
for (int i = 0; i < numberV2; i++)
for (int j = 0; j < numberV2; j++)
matrix2[i, j] = 0;
for (int i = 0; i < E2.Count; i++)
{
matrix2[E2[i].v1, E2[i].v2] = 1;
}
int[,] matrix = new int[6, 6];
drawgraph.fillAdjacencyMatrix(6, E2, matrix);
for(int i = 0; i < 6; i++)
for(int j = 0; j < 6; j++)
Assert.AreEqual(matrix[j,i] , matrix2[j, i]);
}
[TestMethod()]
public void GetBitmapTest()
{
drawgraph = new DrawGraph(500, 500);
drawgraph.drawVertex(150, 150, "a");
Bitmap asd = drawgraph.GetBitmap();
MemoryStream wew = new MemoryStream();
asd.Save(wew, System.Drawing.Imaging.ImageFormat.Png);
Assert.AreEqual(2564, wew.Length);
}
}
}
1


про публікацію авторської розробки
Додати розробку