Розробка уроків до теми «Теорема Піфагора»

РОЗРОБКА УРОКІВ ДО ТЕМИ «ТЕОРЕМА ПІФАГОРА»

 

Методична розробка складається з трьох уроків на теми: «Середні пропорційні відрізки в прямокутному трикутнику», «Теорема Піфагора», «Перпендикуляр і похила, їх властивості». На першому уроці розглядаються метричні співвідношення в прямокутному трикутнику та формуються вміння розв'язувати задачі на застосування цих співвідношень. На етапі засвоєння нових знань і вмінь розв’язуються вправи з підручника, а для закріплення основних понять уроку використовується інтерактивна вправа за комп’ютером.

Для формулювання та доведення теореми Піфагора використовуються розглянуті на першому уроці метричні співвідношення в прямокутнику трикутнику. На засвоєння нових знань і вмінь також виконуються завдання з підручника, а для перевірки передбачено виконання тестових завдань.

Головною метою третього уроку є формування вміння співставляти поняття похилої, перпендикуляра та проекції похилої зі сторонами прямокутного трикутника з подальшим використанням теореми Піфагора.

Уроки розроблені на основі матеріалів підручника [1] та посібника [2].

Тема. Середні пропорційні відрізки в прямокутному трикутнику

Мета:

• навчальна: сформувати поняття середнього пропорційного відрізка; сформувати вміння розв'язувати задачі на застосування метричних співвідношень у прямокутному трикутнику;
• розвивальна: розвивати уміння записувати метричні співвідношення між відрізками прямокутного трикутника та виконувати обчислення невідомих відрізків прямокутного трикутника; формувати вміння орієнтуватися у видозміненій ситуації;
• виховна: виховувати творчу активність, спостережливість, уважність.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання та наочність: підручник, комп’ютери.

 

ХІД УРОКУ

I. ОРГАНІЗАЦІЙНИЙ ЕТАП

 

II. АНАЛІЗ КОНТРОЛЬНОЇ РОБОТИ

 

III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Фронтальне опитування

1. Які види трикутників (за кутами) існують?
2. Які трикутники називають прямокутними?
3. Як називають сторони прямокутного трикутника?
4. Чому дорівнює сума гострих кутів прямокутного трикутника?
5. Що таке висота трикутника?
6. Скільки висот можна провести в будь-якому трикутнику?
7. У трикутнику АВС 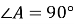. Яку назву мають сторони цього трикутника?
8. Знайдіть кути прямокутного трикутника, якщо один із них дорівнює: а) 45°; б) 70°; в) 92°

 

IV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

Подібність трикутників дозволяє встановлювати низку співвідношень між довжинами деяких відрізків трикутника. Такі співвідношення називають метричними. Спочатку розглянемо декілька допоміжних понять.

 

1. Означення середнього пропорційного відрізка.

Відрізок с називають середнім пропорційним між відрізками a і b, якщо  , тобто c²=ab.

2. Означення проекції катета на гіпотенузу.

Відрізки, на які висота прямокутного трикутника, проведена з вершини прямого кута, ділить гіпотенузу, називають проекціями катетів на гіпотенузу.

 

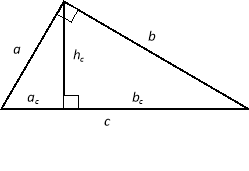3. Метричні співвідношення в прямокутному трикутнику.

У прямокутному трикутнику висота, проведена до гіпотенузи, є середнім пропорційним відрізком між проекціями катетів на гіпотенузу. (Квадрат висоти прямокутного трикутника, проведеної до гіпотенузи, дорівнює добутку проекцій катетів на гіпотенузу)

 

 

У прямокутному трикутнику катет є середнім пропорційним між гіпотенузою та його проекцію на гіпотенузу. (Квадрат катета дорівнює добутку гіпотенузи та проекції цього катета на гіпотенузу)

Висота, проведена до гіпотенузи, дорівнює добутку катетів, поділеному на гіпотенузу.

5. Поділ прямокутного трикутника висотою, проведеною до гіпотенузи.

Висота прямокутного трикутника, проведена до гіпотенузи, ділить трикутник на два подібних прямокутних трикутники, кожен із яких подібний поданому трикутнику.

 

V. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ

Робота за підручником:

1. 510. Знайдіть висоту прямокутного трикутника, проведену з вершини прямого кута, якщо вона ділить гіпотенузу на відрізки завдовжки 2 см і 18 см.
2. 512. Висота прямокутного трикутника, проведена до гіпотенузи, ділить її на відрізки завдовжки 5 см і 20 см. Знайдіть катети трикутника.
3. 513. (самостійно) Висота прямокутного трикутника, проведена з вершини прямого кута, дорівнює 48 см, а проекція одного з катетів на гіпотенузу – 36 см. Знайдіть сторони даного трикутника.
4. 514. Знайдіть катети прямокутного трикутника, висота якого ділить гіпотенузу на відрізки, один з яких на 3 см менший від цієї висоти, а другий – на 4 см більший за висоту.
5. 517. (додаткове завдання) Перпендикуляр, опущений із точки кола на діаметр, ділить його на два відрізки, один з яких дорівнює 4 см. Знайдіть радіус кола, якщо довжина перпендикуляра дорівнює 10 см.

 

VI. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

1. Робота в парах за комп’ютером: https://learningapps.org/display?v=p8chrb8hc18

2. Виконання усних вправ

• Чому дорівнює висота прямокутного трикутника, якщо вона ділить гіпотенузу на відрізки завдовжки 9 см і 16 см? (12 см)
• Проекції катетів прямокутного трикутника на гіпотенузу дорівнюють 7 см і 9 см. Знайдіть довжину більшого катета. (12 см)
• Сторони прямокутного трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть висоту цього трикутника, проведену до гіпотенузи. (4,8 см)

 

VII. ДОМАШНЄ ЗАВДАННЯ

Завдання за підручником: п. 15, вивчити метричні співвідношення, виконати вправи 511, 515.

Додаткове завдання: https://learningapps.org/3233734

 

Тема. Теорема Піфагора

Мета:

• навчальна: сформувати в учнів розуміння змісту теореми Піфагора та її доведення;
• розливальна: розвивати уміння знаходити невідому сторону прямокутного трикутника за двома відомими; розвивати творчі здібності, кмітливість учнів;
• виховна: виховувати інтерес до вивчення математики, уважність, старанність;

Тип уроку: засвоєння нових знань і вмінь.

Обладнання та наочність: підручник, картки.

 

 

ХІД УРОКУ

I. ОРГАНІЗАЦІЙНИЙ ЕТАП

 

II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 

ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Математичний диктант

Варіант 1	Варіант 2
1. Побудуйте трикутник АВС, у якому
∠А = 90°	∠С = 90°
2. Проведіть у трикутнику АВС висоту
АК	СМ
3. Яку назву мають відрізки
ВК і КС?	АМ і МВ?
4. Знайдіть довжину висоти, якщо
ВК = 4 см, КС = 9 см	АМ = 8 см, МВ = 2 см
5. Знайдіть квадрати катетів трикутника АВС

 

ІV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

1. Теорема Піфагора.

Для формулювання та доведення теореми Піфагора скористуємося розглянутими на попередньому уроці метричними співвідношеннями в прямокутнику трикутнику.

Розглянемо прямокутний трикутник з катетами а і b, гіпотенузою с і висотою, проведеною до гіпотенузи h_c. Запишемо для цього трикутника метричні співвідношення для катетів:

 

 

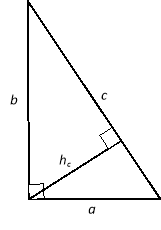
Виконаємо почленне додавання обох частин здобутих рівностей:

 

 

З рівності , маємо

 

Таким чином ми отримали математичний запис теореми Піфагора. Спробуємо перетворити отриману формулу з математичної мови на звичайну:

• У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.

2. Застосування теореми Піфагора до обчислення невідомої сторони прямокутного трикутника за двома відомими.

Нехай a і b – катети прямокутного трикутника, с – його гіпотенуза. Тоді:

або

або

 

V. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ

Робота за підручником:

1. 529.(усно) Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють: 1) 3 см і 4 см; 2) 6 см і 9 см.
2. 530. (усно) Знайдіть катет прямокутного трикутника, якщо його гіпотенуза та другий катет відповідно дорівнюють: 1)15см і 12см; 2) 7 см і 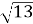см.
3. 532. Сторони прямокутника дорівнюють 9 см і 40 см. Чому дорівнює його діагональ?
4. 534. Бічна сторона рівнобедреного трикутника дорівнює 29 см, а висота, проведена до основи, – 21 см. Чому дорівнює основа трикутника?
5. 536. У колі, радіус якого дорівнює 10 см, проведено хорду завдовжки 16 см. Знайдіть відстань від центра кола до даної хорди.
6. 537.(самостійно) Знайдіть периметр ромба, діагоналі якого дорівнюють 24 см і 32 см.

 

VI. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

Виконання тестових завдань

Варіант 1

1) Знайдіть гіпотенузу прямокутного трикутника, катети якого дорівнюють 8 см і 6 см.
А 14 см	Б 7 см	В 50 см	Г 10 см
2) Знайдіть сторону ромба, діагоналі якого дорівнюють 8 см і 6 см.
А 10 см	Б 14 см	В 5 см	Г 12,5 см
3) Знайдіть висоту рівнобічного трикутника, основа якого дорівнює 24 см, а бічна сторона – 13 см.
А 5 см	Б см	В см	Г 10 см

1-Г. 2-В. 3-А.

Варіант 2

1) Знайдіть гіпотенузу прямокутного трикутника, катети якого дорівнюють 4 см і 3 см.
А см	Б 7 см	В 5 см	Г 12,5 см
2) Знайдіть сторону ромба, діагоналі якого дорівнюють 16 см і 12 см.
А 10 см	Б 20 см	В 18 см	Г 14 см
3) Знайдіть висоту рівнобічного трикутника, основа якого дорівнює 20 см, а бічна сторона – 26 см.
А 25 см	Б 24 см	В см	Г см

1-В. 2-А. 3-Б.

Бліцопитування

1. Чи правильно, що трикутник зі сторонами 7, 24, 25 є прямокутним?
2. У трикутнику ВМL ВМ² =ВL² + LМ². Укажіть прямий кут цього трикутника.
3. Дві менші сторони трикутника дорівнюють 9 см і 12 см. Чому має дорівнювати найбільша сторона трикутника, щоб він був прямокутним?

 

VII. ДОМАШНЄ ЗАВДАННЯ

Завдання за підручником: п. 16, вивчити теорему, виконати вправи 531, 535.

Додаткове завдання: https://learningapps.org/3194326

 

Тема. Перпендикуляр і похила, їх властивості

Мета:

• навчальна: сформувати поняття перпендикуляра, похилої, проекції на пряму, домогтися засвоєння їх властивостей; сформувати вміння розв'язувати задачі, які передбачають застосування означення та властивостей перпендикуляра, похилих та їх проекцій;
• розвивальна: формувати вміння виділяти головне в досліджуваному матеріалі; розвивати абстрактне мислення;
• виховна: виховувати толерантність, самостійність, дисциплінованість.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання та наочність: підручник, картки

 

ХІД УРОКУ

I. ОРГАНІЗАЦІЙНИЙ ЕТАП

 

II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

 

ІІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Фронтальне опитування

1. Укажіть катети та гіпотенузу прямокутного трикутника, якщо його сторони дорівнюють:

1) 10 см, 6 см, 8 см; 2) 10 см, 24 см, 26 см.

2. Катети одного трикутника дорівнюють 5 см і 12 см, а другого – 12 см і 16 см. Гіпотенуза якого із трикутників більша? Чи можна дати відповідь на запитання, не виконуючи обчислень?

3. Що називають перпендикуляром, проведеним із точки до прямої? Якою геометричною фігурою є перпендикуляр?

4. Яке із наведених тверджень неправильне?

• Довжина відрізка є додатним числом.
• У прямокутному трикутнику довжина гіпотенузи більша за довжину будь-якого з катетів.
• Відстань від точки до прямої – це довжина перпендикуляра, проведеного з точки до прямої.
• Із точки А до прямої т можна провести безліч перпендикулярів.

 

ІV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

1. Означення похилої, проведеної з точки до прямої.

Нехай точка А не лежить на прямій а, АВ – перпендикуляр до цієї прямої. Будь-який відрізок, який сполучає точку А з точкою прямої а і не збігається з перпендикуляром, називають похилою до прямої а.

2. Означення проекції похилої на пряму.

Відрізок прямої а, обмежений основами перпендикуляра і похилої, називають проекцією похилої на подану пряму.

3. Властивості перпендикуляра, похилих та їх проекцій.

Нехай із однієї точки до прямої проведено перпендикуляр і похилі. Тоді:

• будь-яка похила більша за перпендикуляр і більша за свою проекцію на подану пряму;
• рівні похилі мають рівні проекції, і навпаки: якщо проекції двох похилих рівні, то рівні й самі похилі;
• більша похила має більшу проекцію, і навпаки: з двох похилих більша та, яка має більшу проекцію.

 

V. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ

1. Із точки, що знаходиться на відстані 6 см від прямої, проведено дві рівні похилі до цієї прямої. Відстань між основами похилих дорівнює 16 см. Знайдіть довжину похилих.
2. Із точки до прямої проведено дві похилі, довжина однієї з них дорівнює 26 см, довжина її проекції – 24 см. Знайдіть довжину другої похилої, якщо вона утворює з прямою кут 45°.
3. (додатково) Із точки до прямої проведено дві похилі, довжини яких дорівнюють 5 см і 7 см, а різниця їх проекцій дорівнює 4 см. Знайдіть відстань між основами похилих.
4. 558. Із точки до прямої проведено дві похилі, довжини яких відносяться як 5:6, а проекції цих похилих на пряму дорівнюють 7 см і 18 см. Знайдіть відстань від даної точки до цієї прямої.
5. 556.(самостійно) Сторони тупокутного трикутника дорівнюють 29 см, 25 см і 6 см. Знайдіть висоту трикутника, проведену до меншої сторони.

 

VI. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

1. Виконання тестових завдань

1. Нехай MN – перпендикуляр, опущений із точки М на пряму а, а Р і R – будь-які точки прямої а (мал. 1). Яке твердження неправильне?

1. Відрізки MP і MR називаються похилими, проведеними з точки М до прямої а.
2. PN і RN  – проекція похилих MP і  MR.
3. Якщо PN < NR, то MP < MR.
4. З даної точки поза прямою можна провести до неї три похилі однакової довжини.

2. Похила довжиною 10 см, проведена з даної точки до прямої, має проекцію довжиною 6 см. Обчисліть довжину перпендикуляра, опущеного з тієї самої точки на пряму.

1) 9 см; 2) 8 см; 3) 7 см; 4) 6 см.

мал.1

мал.2

 

3. Із точки К до прямої а проведено перпендикуляр і похилу довжиною відповідно 15 см і 17 см. Знайдіть проекцію похилої.

1) 6 см; 2) 7 см; 3) 8 см; 4) 9 см.

4. У трикутнику ABC 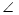C = 90°, CD 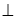AB, AC = 13 см, CD = 5 см, AB = 20 см (мал.2). Знайдіть проекцію катета СВ на гіпотенузу АВ.

1) 5 см; 2) 6 см; 3) 7 см; 4) 8 см.

5. Відрізок MN дорівнює 25 см. Його кінці лежать від прямої а на відстані 4 см і 11 см. Знайдіть проекцію відрізка MN на цю пряму.

1) 22 см; 2) 23 см; 3) 24 см; 4) 20 см.

 

Бліцопитування

1. Чи можна вказати проекцію поданої похилої, не побудувавши перпендикуляр?
2. Яку геометричну фігуру утворюють перпендикуляр і похила, проведені з однієї точки, разом із проекцією похилої?
3. Скільки похилих можна провести з поданої точки до поданої прямої?

 

VII. ДОМАШНЄ ЗАВДАННЯ

Завдання за підручником: п. 16, повторити теорему Піфагора, виконати вправу 559. Вивчити конспект

 

 

 

Список використаних джерел

1. Мерзляк А. Г. Геометрія : підруч. для 8 кл. загальноосвіт. навч. закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. — X.: Гімназія, 2016. — 208 с.: іл.
2. Старова О. О. Геометрія. 8 клас / О. О. Старова — Х. : Вид. група «Основа», 2016. — 144 c. — (Серія «Мій конспект»)