Розробка уроку на тему "Геометричні побудови"

Тема. Геометричні побудови

Мета: засвоєння учнями алгоритму побудови прямої, яка перпендикулярна до даної і проходить через дану точку на даній прямій (або поза даною прямою), і алгоритму побудови прямої, яка паралельна даній і проходить че­рез дану точку поза даною прямою; вироблення вмінь відтворювати вивчені алгоритми і виконувати дії, описані в них; відпрацювання навичок володіння креслярськими інструментами (для вимірювання та побудови прямих, відрізків, кіл та дуг кіл) і навичок аргументовано міркувати з посиланням на вивчені означення, властивості і ознаки рівних відрізків, кутів та трикутників (при доведенні пра­вильності здійснених побудов).

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таб­лиця № 22 «Геометричні побудови».

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання   

Зібрати аркуші із виконаним домашнім завданням; за при­готованими заздалегідь на дошці рисунками прокоментувати виконання задачі № 604 (або в разі необхідності всі задачі).

III. Формулювання мети і завдань уроку   

Для створення відповідної мотивації навчальної діяльності, тобто для усвідомлення значення нового на уроці матеріалу, вчитель може спонукати учнів до певної узагальнюючої робо­ти, а саме: запропонувати їм назвати відношення між двома прямими, означення, властивості і ознаки яких вони вивчали у сьомому класі, і назвати ті відношення між будь-якими двома прямими, які вони найчастіше можуть бачити навколо себе. Скоріше за все учні дадуть правильні відповіді, а тому мета уроку буде цілком зрозуміла учням.

IV. Актуалізація опорних знань і вмінь учнів

Усні   вправи

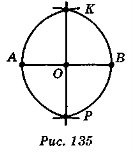
1. На дошці виконано побудову середини відрізка АВ — точки О (рис. 135). Прокоментуйте цей спосіб побудови. Що можна сказати про довжини відрізків АК, ВК, АР і ВР, виходячи з побудови? Визначте вид трикутників АКВ, АРВ, РАК, КВР. Які властивості має відрізок ОК
   в трикутнику АКВ? Відрізок ОР в трикутнику АРВ? Які ще відрізки і в яких трикутниках на цьому рисунку мають ті самі властивості?

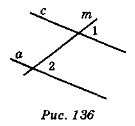
2. На рис. 136 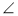1 = 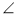2. Що можна стверджувати щодо взаємного розміщення прямих а і с? чому?

V. Засвоєння нових знань    

План вивчення нового матеріалу

1. Алгоритм  побудови  прямої,   що  проходить  через  дану точку поза даною прямою, перпендикулярно до даної.
2. Алгоритм побудови прямої, перпендикулярної до даної, що проходить через дану точку на даній прямій.
3. Алгоритм побудови прямої, що проходить через дану точку поза даною прямою, паралельно даній прямій.

Методичний   коментар

Перші два алгоритми (див. план) традиційно вивчають у сьомому класі. Вони є не тільки основою для успішного по­дальшого вивчення шкільного курсу геометрії, але й елементом математичної культури учнів. Ці алгоритми разом з тими, що вивчалися на попередньому уроці, є важливими засобами для розв'язування задач на побудову. Зауважимо, що запропонова­ний спосіб побудови прямої, яка паралельна даній прямій і про­ходить через дану точку поза прямою, взагалі в традиційному підручнику не розглядався (хоча побудова прямої, паралельної даній, є одним із етапів розв'язування досить великої кількості задач на побудову — наприклад, задачі на побудову методом подібності). При вивченні третього алгоритму варто було б ще раз звернути увагу учнів на той цікавий факт, що незважаючи на нескінченну кількість прямих, що перетинають дану пряму і які можуть проходити через задану точку, пряма, паралельна даній (шукана), — єдина!

VI. Первинне усвідомлення матеріалу

Усні   вправи

№ 611 (див. підручник).

Графічні   вправи

1. За підручником: № 605 (застосувати алгоритм побудо­ви прямої, перпендикулярної до даної), № 610 (перед розв'язанням обговорити особливості положення висот трикутника залежно від виду його кутів), № 612 (засто­сувати алгоритм побудови прямої, паралельної даній).
2. Додатково можна запропонувати учням розв'язати таку задачу:

Як поділити навпіл відрізок, якщо:

а) він зображений на краю аркуша паперу (дошки);

б) він у кілька разів більше найбільшого розхилу циркуля?

(Розв'язання цих задач подано на рис. 137 (а, б).

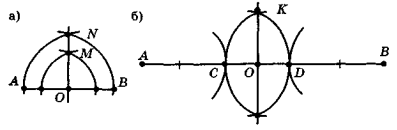
Рис. 137

VII. Підсумки уроку    

Контрольні запитання № 1—6 (див. підручник с. 157).

VIII. Домашнє Завдання    

1. § 20 — записати задачі № 5, 6 у вигляді алгоритму і вивчити його.
2. Використовуючи алгоритми, розв'язати задачі № 606, 608, 609 (оформити як практичну роботу на нелінованому папері).
3. Повторити: означення кола, поняття «рівновіддалені точки». Розв'язати: з самостійної роботи 3 варіант 4 (№ 3), с. 99 підручника.