Розробка уроку на тему "Прямокутний трикутник"

Тема. Прямокутний трикутник

Мета: домогтися засвоєння учнями змісту властивості прямо­кутного трикутника з гострим кутом 30° та оберненого твердження, а також схеми їх доведення; сформувати в учнів уміння відтворювати зміст названої властивості і застосовувати цю властивість при розв'язуванні задач; удосконалювати вміння використовувати набуті раніше знання для розв'язування задач із прямокутним трикут­ником.

Тип уроку: засвоєння знань, вироблення вмінь, удосконалення на­вичок.

Обладнання: набір демонстраційного креслярського приладдя, табли­ці № 15 «Прямокутний трикутник» і № 16 «Прямокутний трикутник з гострим кутом 30°», роздавальний матеріал (моделі рівносторонніх трикутників).

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Особливо ретельно слід перевірити правильність виконання вправ № 456 і № 4 (б), тому їх розв'язання слід обговорити з учнями. Для цього можна залучити «сильних» учнів. У той час, коли на дошці будуть записувати розв'язання цих задач, решта учнів працюватиме над виконанням завдань математич­ного диктанту (мета проведення диктанту — перевірка рівня засвоєння основних понять попереднього уроку).

Математичний   диктант   №   11

Варіант 1

1. Закінчіть речення:  «Трикутник, у якого є прямий кут, називається...»
2. У прямокутному трикутнику один із кутів дорівнює 47°. Чому дорівнюють два інші його кути?
3. Закінчіть речення: «Сторона прямокутного трикутника, що лежить проти прямого кута, називається...»
4. Гіпотенузи двох прямокутних трикутників рівні. Один із кутів першого трикутника дорівнює 40°, а один із кутів другого трикутника дорівнює 50°. Чи рівні ці трикутники? чому?
5. У трикутнику ABC кут А прямий. Як називається в цьому трикутнику сторона АВ?
6. У прямокутних трикутниках ABC і МТР рівні катети ВС і ТР і гіпотенузи АВ і МТ. Що можна сказати про ці трикутники? чому?

Варіант 2

1. Як називається трикутник, у якому кут дорівнює 90°?
2. У прямокутному трикутнику один із кутів дорівнює 67°. Чому дорівнюють два інші його кути?
3. Закінчіть речення: «Сторона прямокутного трикутника, прилегла до прямого кута, називається...»
4. Гіпотенузи двох прямокутних трикутників рівні. Один із кутів першого трикутника дорівнює 20°, а один із кутів другого трикутника — 70°. Чи рівні ці трикутники? чому?
5. У трикутнику ABC кут В прямий. Як називається в цьому трикутнику відрізок ВС?
6. У прямокутних трикутниках ABC і МОК рівні гіпотенузи АВ і МО і катети ВС і ОК. Що можна сказати про ці трикутники? чому?

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів

Створенню умов для успішної мотивації навчальної діяль­ності учнів може сприяти запропонована учням практична робо­та (з трьома готовими моделями рівносторонніх трикутників).

Практична   робота

Завдання   1

Виміряйте довжини сторін кожного з даних трьох трикут­ників. Що ви можете сказати про міри кутів цих трикутників? Визначте за цими вимірами вид трикутників. Чи є дані три­кутники трикутниками одного виду?

Завдання   2

Проведіть на даних моделях по одній медіані, висоті та бісектрисі відповідно на першому, другому та третьому трикут­никах. На трикутники якого виду поділили проведені відрізки кожний з трикутників? Що вам відомо після виконання першого завдання про сторони цих трикутників? Обчисліть кути цих трикутників. Що ви помітили? Як це можна пояснити?

Завдання   3

Використайте властивість бісектриси рівнобедреного три­кутника, проведеної до основи, щоб обчислити одну з невідо­мих сторін трикутників, утворених під час виконання другого завдання. Як називаються ці сторони в утворених трикутниках? Узагальніть свої висновки, висунувши гіпотезу.

Після виконання останнього третього завдання самі учні усвідомлюють проблему: необхідність доведення або спростуван­ня висунутої гіпотези і розв'язання цієї проблеми є основною дидактичною метою уроку.

IV. Актуалізація опорних знань і вмінь учнів

Під час розв'язування запропонованих вище завдань учні активізують свої знання,,їм доводиться згадати означення прямокутного трикутника, а також означення та властивості бісектриси (медіани, висоти) рівнобедреного трикутника, про­веденої до основи.

V. Засвоєння нових знань

План вивчення нового матеріалу

1. Властивість катета, що лежить проти кута 30°; доведення цієї властивості (опорна задача с. 118).
2. Обернене твердження; доведення оберненого твердження.

Методичний   коментар

При доведенні опорного факту про властивість катета, що лежить проти кута 30°, ми посилаємося на ознаку рівностороннього трикутника і властивість бісектриси рівнобедреного трикутника (як це робилося традиційно).

Після доведення властивості доводимо обернене твердження, яке часто використовується під час розв'язування задач на об­числення кутів прямокутного трикутника (через співвідношення катета і гіпотенузи).

Якщо є можливість, то можна запропонувати учням довести також твердження, яке є оберненим до властивості кутів пря­мокутного рівнобедреного трикутника (задача № 212).

Засвоєння нових знань відбуватиметься більш успішно, якщо використовуватиметься відповідна наочність: табли­ці № 15 і 16.

Таблиця № 16

Прямокутний трикутник з гострим кутом  30°

VІ. Первинне усвідомлення навчального матеріалу

Усні   вправи

1. За даними рис. 110 знайдіть у кожному трикутнику невідомий елемент х.

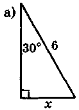
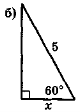
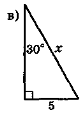
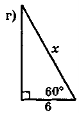
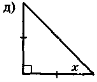
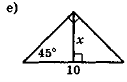
Рис. 110

2. Гіпотенуза прямокутного трикутника дорівнює 10 см, один із гострих кутів цього трикутника вдвічі більший за інший. Знайдіть катет, прилеглий до більшого гострого кута цього трикутника.

VII. Вироблення вмінь

Письмові   вправи

1. № 1 (а, б), с. 128 (задачі за готовими рисунками) і до­даткові задачі.
2. Додаткові задачі.

1) Один із кутів прямокутного трикутника дорівнює 60°, а різниця між гіпотенузою і катетом, прилеглим до даного кута, становить 6 см. Знайдіть гіпотенузу й катет цього трикутника.

2) Доведіть рівність прямокутних трикутників за катетом і висотою, проведеною до гіпотенузи.

VIII. Підсумки уроку

Запитання   до   класу

Чи існують трикутники, зображені на рис. 111?

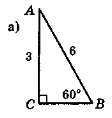
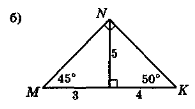
Рис. 111

IX. Домашнє завдання

1. § 15 — повторити означення та ознаки рівності прямо­кутних трикутників і вивчити твердження, що містяться в опорних задачах.
2. Письмово: N° 457 та № 2 (а), с. 128 (задачі за готови­ми рисунками), і № 454 (на застосування властивостей прямокутного рівнобедреного трикутника).
3. На повторення: № 2 (а, б), с. 100.