Розробка уроку на тему "Прямокутний трикутник"

Тема. Прямокутний трикутник

Мета: домогтися засвоєння учнями змісту таких понять, як перпендикуляр, проведений з точки до прямої; похила, проведена з точки до прямої; проекція похилої на пряму, а також установити логічний зв'язок між цими поняттями та поняттям прямокутного трикутника; вивчити власти­вості перпендикуляра, похилої та проекції, а також зміст понять про відстань від точки до прямої і відстань між двома паралельними прямими. Сформувати вміння: відтворювати зміст вивчених понять, застосовувати ви­вчені поняття та властивості прямокутного трикутника для розв'язування задач на обчислення відстаней від точки до прямої та між паралельними прямими, а також для порівняння сторін трикутника.

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання: набір демонстраційного креслярського приладдя, таб­лиця № 17 «Відстані на площині».

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Розв'язання задач № 2 (с. 128) і № 2 (а, б), с. 100 учні пере­віряють під час роботи з готовими розв'язаннями, записаними на дошці заздалегідь.

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів

Позитивній мотивації діяльності учнів може посприяти запропоноване учням завдання.

Завдання

На площині дано точку А. Як знайти відстань від цієї точки до:

а) деякої точки В;

б) деякої прямої а?

Обговорення цього практичного завдання дає учням змо­гу розв'язати цю проблему: яким чином можна однозначно визначити відстань від точки до прямої? В ході обговорення може виникнути і інша проблема: визначення відстані між паралельними прямими. Пошук відповідей на поставлені запитання і встановлення логічного зв'язку цих запитань з матеріалом попередніх уроків (прямокутний трикутник і його властивості) — є по суті основною дидактичною метою уроку.

IV. Актуалізація опорних знань і вмінь учнів

Усні   вправи

1. Дано: ОС — бісектриса кута АОВ, CD перпендикулярно ОА, CF перпендикулярно ОВ (рис. 112). Доведіть: CD = CF .
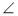2. Дано: M = 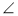B = 90°, MC = BC (ряс. 113). Доведіть: АВ = МН.
3. У трикутнику ABC АВ = 3,3 см, ВС = 3 см 5 мм, АС = 5 дм. Назвіть найбільший кут трикутника.
4. У трикутнику ABC AB < BC, 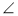A < 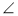B. Назвіть наймен­ший кут трикутника.

V. Засвоєння знань

План вивчення нового матеріалу

1. Поняття перпендикуляра, похилої, проведеної з точки до прямої, і проекції похилої; їх зв'язок з елементами прямокутного трикутника.
2. Властивості перпендикуляра і похилої, похилої і проек­ції.
3. Відстань між геометричними фігурами; відстань від точки до прямої; відстань між паралельними прямими.
4. Рівність трикутників.

Таблиця № 17

Відстані на площині

Методичний   коментар

За традиційним підручником матеріал уроку вивчається у восьмому класі в темі «Наслідки з теореми Піфагора» більш детально: крім понять перпендикуляра, похилої та проекції вивчаються поняття основи перпендикуляра та основи похи­лої, причому від учнів вимагається володіння всіма названими термінами. На відміну від традиційного підходу до вивчення питання про властивості перпендикуляра, похилої та її проекції в новому посібнику обґрунтування цих властивостей ведеться через нерівність трикутників та наслідки з неї (див. § 16).

VI. Первинне усвідомлення матеріалу

Усні   вправи

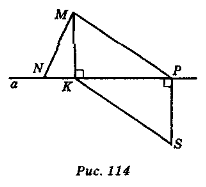
1. На рис. 114 знайдіть і назвіть перпендикуляри, проведені з певної точки до прямої а, похилі та їх проекції.

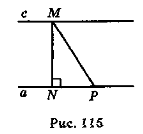
2. На рис. 115 знайдіть і назвіть відстані: від точки М до прямої а; між паралельними прямими а і с.
3. На рис. 116 знайдіть довжини відрізків х.

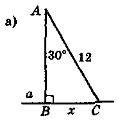
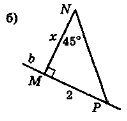
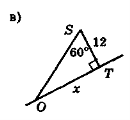
Рис. 116

VII. Вироблення вмінь

Письмові   вправи

На закріплення матеріалу уроку виконати вправи № 459, 460, 461, 477, 479, 483.

Методичний   коментар

При розв'язуванні вищезазначених вправ слід вимагати від учнів активного використання термінології, вивченої на уроці.

VIII. Підсумки уроку 

Запитання   до   класу

Чи є правильними зображення трикутників на рис. 117?

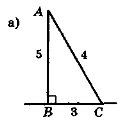
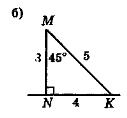
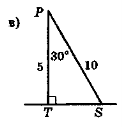
Рис 117

IX. Домашнє завдання

1. § 15—16 — вивчити означення і властивості перпенди­куляра, похилої та проекції, нерівність трикутників.
2. Письмово: № 1, 2, 3 (див. нижче), № 478, 484 (за під­ручником).
3. На повторення: № 2 (б), с. 128.

Задача   №   1

У трикутнику МРК МК = 8 см, M = 60°, K = 90°. Знайдіть:

а) відстань від точки М до прямої КР;

б) проекцію похилої MP на пряму МК;

в) довжину похилої MP.

Задача   №   2

У трикутнику МРК M < P = 45°, відстань від точки К до прямої MP дорівнює 12 см. Знайдіть:

а) проекцію відрізка МК на пряму MP;

б) довжину найбільшої сторони трикутника МРК.

Задача   №  3

Знайдіть довжину відрізка січної, що перетинає дві пара­лельні прямі, якщо відстань між цими паралельними прями­ми 40 см, а січна перетинає одну з паралельних прямих під кутом 30°.