Розробка уроку на тему "Сума кутів трикутника"

Тема. Сума кутів трикутника

Мета: домогтися засвоєння учнями змісту теореми про суму кутів трикутника та змісту її доведення, а також деяких висновків з цієї теореми; виробити в учнів уміння засто­совувати зміст теореми і висновків з неї, а також викорис­товувати сформульовані твердження при розв'язуванні задач на знаходження градусних мір кутів трикутника.

Тип уроку: засвоєння знань, вироблення вмінь.

Обладнання: набір демонстраційного креслярського приладдя; таб­лиця № 10 «Сума кутів трикутника».

Хід уроку

І. Організаційний етап    

ІІ. Перевірка домашнього завдання    

Оскільки матеріал попереднього уроку має бути опрацьо­ваний на уроці та закріплений вдома, перевірку домашнього завдання учні здійснюють самостійно за готовим зразком.

III. Формулювання мети і завдань уроку. Мотивація навчальної діяльності учнів

Для успішної мотивації діяльності учнів учитель спонукає учнів до повторення основних відомостей про трикутник (як одну з багатьох геометричних фігур) і формулює проблему: чи можна побудувати трикутник з наперед заданими мірами кутів і якщо так, то чи існують які-небудь обмеження щодо градусних мір цих кутів (наприклад, чи можна побудувати трикутник, у якого всі три кути тупі, або всі три кути прямі, тощо). Після усвідомлення учнями суті проблеми вчитель разом з учнями формулює основну мету уроку — використавши отримані раніше знання, сформулювати властивість кутів трикутника, довести справедливість сформульованої теореми і навчитися використовувати доведене твердження при розв'язуванні задач відповідного змісту.

IV. Актуалізація опорних знань і вмінь учнів

Усні   вправи

1. Чи є на рис. 52 пари суміжних кутів? Назвіть їх.

2. Вставте пропущені рисунки і записи в таблиці на рис. 53.

Рис. 53

V. Засвоєння нових знань  

План вивчення нового матеріалу

1. Теорема про суму градусних мір кутів трикутника та її доведення.
2. Наслідки з теореми.
3. Ще раз про класифікацію трикутників за градусною мірою його кутів.

Методичний   коментар

Як і в традиційному підручнику, в даному посібнику тео­рема про суму кутів трикутника подається після теми «Влас­тивість паралельних прямих» і її доведення, що здійснюється із посиланням на властивість кутів, утворених при перетині двох паралельних прямих січною, добре засвоюється учнями і, зазвичай не викликає в учнів труднощів. Звернімо увагу на те, що в даному посібнику за основні кути при перетині па­ралельних прямих січною прийнято внутрішні різносторонні кути і саме на їх властивість посилаються автори підручника при доведенні теореми (доведення із посиланням на власти­вості інших кутів можна розглянути як інший можливий варіант на уроці або запропонувати учням знайти цей варіант самостійно). Але для кращого усвідомлення учнями змісту і доведення теореми (за умови відповідної підготовки учнів) роботу над теоремою можна організувати у вигляді невеликої практичної роботи.

Практична   робота

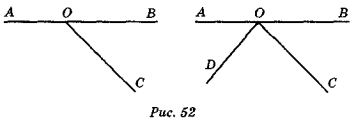
1. Назвіть пари вертикальних кутів та пари внутрішніх різносторонніх кутів при паралельних прямих а і b і січ­них с і d (рис. 54).

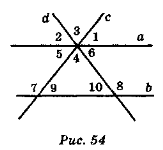
2. Що можна сказати про кути кожної пари (див. п. 1)?
3. Укажіть на рис. 54 суміжні кути з вершиною в точці В. Чому дорівнює сума їх градусних мір?
4. Порівняйте отриману в п. З суму з сумою градусних мір кутів трикутника. Зробіть висновок.

Для підготовки учнів до сприйняття висновку з теореми можна запропонувати учням знайти відповіді на запитання.

а) Яким мав би бути кут трикутника, якби кожний з двох інших його кутів був прямий?

б) Яким мав би бути кут трикутника, якби два інші його кути мали градусну міру 100°  і  120°  відповідно?

в) Яким мав би бути кут трикутника, якби один із двох інших кутів був тупий, а другий — прямий?

Якщо учні обґрунтовують свої відповіді, то доведення на­слідку з теореми про суму кутів трикутника буде узагальненням проведених міркувань.

Як квінтесенція роботи з вивчення нового матеріалу демонс­трується таблиця № 10 «Сума кутів трикутника».

Таблиця №10

Питання про види трикутників за градусною мірою його кутів уже вивчалось у сьомому класі, але на даному уроці відповідь на нього має «вдосконалений вигляд», а саме — вид трикутника визначається за градусною мірою найбільшого кута.

Останній момент, на якому слід зосередити увагу учнів на уроці — це нарешті дозвіл розуміти під поняттям кута як гео­метричну фігуру, так і його градусну міру.

VI. Первинне усвідомлення матеріалу   

Задачі, які винесено на урок, можна умовно поділити на дві групи:

Перша група — на безпосереднє застосування теореми — № 289, 290, 296, 297 (а), додаткова № 1: знайти всі кути три­кутника, якщо один із них удвічі менший від другого і на 20° більший за третій.

Друга група — на застосування наслідку — № 291, 300.

VII. Підсумки уроку    

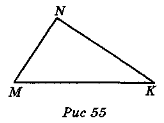
Яке з тверджень неправильне (рис. 55)?

а) M + N = 180° - K;

б) M + N + K = 180°;

в) Якщо  M > 90°, то і  N > 90°.

VIII. Домашнє завдання

1. § 10, с. 81 — вивчити зміст, доведення теореми 8 і на­слідок з неї.
2. Письмово:

1) Знайти кути трикутника, якщо їх градусні міри від­носяться як 2 : 7 : 9.

2) Накресліть трикутник ABC з тупим кутом А. Про­ведіть висоту BD і визначте вид трикутника ABD за градусною мірою кутів. Виміряйте кути BAD, ABC, АСВ, ВАС. Як пов'язана градусна міра кута BAD з гра­дусними  мірами  виміряних  кутів  трикутника ABC?

3) № 295, 297 (б).