розробка уроку на тему " Відсоткові розрахунки. Формула складних відсотків"

Тема уроку. Відсоткові розрахунки. Формула складних відсотків.

 

Мета уроку: повторити формули розв'язування основних задач на відсотки. Продовжити роботу над виробленням умінь застосовувати вивчені формули для розв'язування задач на відсоткові розрахунки, домогтися засвоєння учнями змісту: означення поняття «складні відсотки»; формули складних відсотків. Здійснити взаємозв’язок відсоткових розрахунків з реальним життям; розвивати логічне мислення, просторову уяву; виховувати почуття відповідальності, самостійність

Тип уроку: вивчення нового матеріалу.

Наочність та обладнання: опорний конспект,  ноутбук, роздатковий матеріал.

 

Епіграф:  «Знання лише тоді знання, коли воно отримане  зусиллям розуму, а не пам’яті»

                                                                                                                Л.М.Толстой.

 

ХІД УРОКУ

I. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання

1. Наявність Д/З перевіряє вчитель
2. Перевірка  Д/З (завдання з ДПА 9клас) один учень біля дошки,  решта за зразком

СЛАЙД 2,3

Задача. З куска жерсті розміром 48*30см  виготовили коробку з площею основи 1008 см².Визначити  висоту жерстяної коробки.

Розв’язання.

 (30 - 2х)(48 - 2х) = 1008

2(15 - х)2(24 - х) = 1008

(15 - х)(24 - х) = 252

1524 - 24х - 15х + х²– 252 = 0

360 - 39х + х² – 252 = 0

х²- 39х + 108 = 0

D = 1089 ; √ D = 33

х₁==3; х₂ ==36 – не задовольняє умову задачі

Відповідь: 3 см.

III. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

 

Він дві різні назви має,

Його бухгалтер поважає,

У бізнесі торгівлі – всюди

З ним звикли справу мати люди.

Виконує він скрізь роботу.

А називається …(відсоток).

А яку іншу назву має відсоток?

Вступне слово вчителя

    Шановні учні! Україна має безліч економічних проблем,розв’язувати які доведеться вам ,майбутнім випускникам школи. Тому кожному з вас потрібна фундаментальна  загальна підготовка.

Багатьом фахівцям доводиться виконувати обчислення за умови, що деякі значення виражено у відсотках. Коротко їх називають відсотковими розрахунками.

Сьогодні на уроці ми повторимо методи розв’язування задач на відсотки та ознайомитесь  зі «складними відсотками»

 Лекція вчителя  Дуже часто знання з математики допомагають при вивченні інших суміжних предметів. Досить часто на уроках хімії,фізики,географії вам доводиться зустрічатися з задачами на відсотки. Після сьогоднішнього уроку розв’язувати вам такі задачі стане значно простіше.Відсотки – одне з математичних понять, які часто зустрічаються у повсякденному житті. Слово «процент» походить від латинського pro centum, що означає «від сотні», звідси і дві назви – процент та відсоток. Відсоток означається як сота частина деякої величини. У практиці ми досить часто маємо справу з сотими частинами (копійка, сантиметр, ар), а тому соті дістали спеціальний знак % для їх позначення на письмі. Цей символ % виник у XV столітті в Італії. Вивчати відсотки почали дуже давно.  Ще у ХІІІ – ХVI столітті усі підручники приділяють значну увагу відсотковим обчисленням. Уже в 1494 році користувалися відсотковими таблицями, які підприємства тримали в секреті.

СЛАЙД 4

Спочатку відсотки використовували тільки при фінансових операціях (прибутки з капіталу, сплата внесків, касові операції). Але згодом вони знайшли широку область застосування. Їх використовують для характеристики виконання виробничих планів, визначення зростання чи зниження продуктивності праці, режиму економії, собівартості і якості продукції. У відсотках ми виражаємо вологість повітря, жирність молока, вміст солі у розчині, кількість відсутніх/присутніх учнів у класі і т.д. Відсотки ми часто використовуємо у шкільних курсах, зокрема у математиці та фізиці під час обчислення відносної похибки вимірювання, у хімії при обчисленні концентрації розчинів.

Тому знання відсотків та загальні навички розв’язування типових задач на відсотки необхідне кожній людині.

 Для розв’язування задач на відсотки слід уміти записувати будь-яке число у вигляді відсотка і розв’язувати обернену задачу – виражати відоме число відсотків у вигляді дробового чи цілого числа.

Для найпростіших задач на відсотки уведемо таке позначення: х – деяка величина, що приймається за 100% (ціле), у - її частина, яка виражається числом відсотків р%.  Залежно від того, що невідоме – х, у чи р найпростіші задачі на відсотки можна розділити на три види:

СЛАЙД 5                     Знаходження відсотків від числа.

Щоб знайти відсоток від числа, треба цей відсоток записати десятковим дробом і дане число помножити на здобутий дріб.

 

СЛАЙД 6                  Знаходження числа за його відсотком.

Щоб знайти число за його відсотком, треба відсоток записати у вигляді десяткового дробу і розділити дане число на цей дріб.

СЛАЙД 7       Знаходження відсоткового відношення двох чисел.

Щоб знайти, скільки відсотків  складає перше число  від другого числа, треба перше число поділити на друге  і результат помножити на 100%

СЛАЙД 8      Основні формули відсотків

                                                    10 % від х = 0,1х

0,7 від х = 70% від х

Збільшити х на 15%:

х+0,15х

Зменшити х на 38%:

х – 0,38х

На уроках хімії часто доводиться розв’язувати задачі на складання пропорції

СЛАЙД 9        Пропорція:     a – 100%

                                             b –   c %

Наведення прикладів

СЛАЙД 10     Задача 1. Зимова куртка коштувала 800 грн. Весною ціну куртки знизили на 10%. Але продали її тільки тоді, коли нову ціну знизили ще на 10%. На скільки відсотків ціна, за яку продали куртку, менше від початкової?
Розв’язання. Після першого зниження ціну знизили на 800*0,1=80 (грн.) і куртка стала коштувати  800-80=720 (грн.)
Після другого зниження ціну зменшили на 720*0,1=72(грн.)
В результаті двох знижень ціна куртки зменшилась на 80+72=152 (грн.)
152грн. від 800грн. складає  152/800*100%=19%.
Отже, початкову ціну знизили на 19%.
Відповідь: 19%. 

СЛАЙД 11      Задача 2. Вкладник зняв зі свого рахунку в банку 20% всіх грошей , а на наступний день зняв 10% залишку. Після цього на його рахунку залишилося 360 грн. Скільки грошей було на рахунку спочатку?
Розв’язання. Нехай на рахунку вкладника спочатку було х грн. Після першого зняття грошей н а рахунку залишилося
100%-20%=80% грошей початкового  вкладу.
Із нової суми було знято 80%*0,1=8% початкового вкладу.
Вкладник зняв за два рази 20%+8%=28% початкового вкладу, а на рахунку залишилося 100%-28%=72%.
                                        360грн.-72%
                                          х грн.-100%

=500(грн.)
Відповідь:500 грн.

СЛАЙД 12         Задача 3. Є два сплави з 30 і 10-відсотковим вмістом міді. Скільки кілограмів кожного сплаву потрібно взяти, щоб отримати 6кг нового сплаву з 15-відсотковим вмістом міді?
Розв’язання. Нехай потрібно взяти х кг першого сплаву (з 30-відсотковим вмістом міді). Тоді другого потрібно взяти (6-х) кг.
Перший сплав містить 30% міді, а другий-10%. Тому Х кг першого сплаву містить 0,3х кг міді, а (6-х) кг другого сплаву-0,1(6-х) кг міді. Новий сплав повинен містити 0,3х+0,1(6-х) кг міді. З іншого боку, 6 кг нового сплаву повинен містити 15%, або 6*0,15=0,9(кг) міді. Отримуємо рівняння:
                                        0,3х+0,1(6-х)=0,9
Розв’язавши рівняння, знайдемо: х=1,5
Отже, потрібно взяти 1,5кг першого сплаву і 6-1,5=4,5(кг) другого сплаву.
Відповідь: 1,5 кг ;4,5 кг.                   

СЛАЙД 13      Банківскі відсотки. Формула складних відсотків

А₀- початковий капітал, р% річних

рік	Нарахована сума	Нарахований капітал
1й	А0	А0+ А0 = А0(1+ )
2й	А0(1+ ) 	А0(1+ )+ А0(1+ )  = А0(1+ ) (1+)= А0(1+ )2
3й	А0(1+ )2	А0(1+ )2+ А0(1+ )2 = А0(1+ )2 (1+)= А0(1+ )3
nй		А0(1+ )n

СЛАЙД 14  Формула простих відсотків 

A_n=А₀(1+ )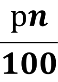

СЛАЙД 15      Формула складних відсотків

A_n=А₀(1+ 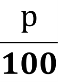)ⁿ

 

VI. Узагальнення і систематизація вивченого матеріалу

1. Технологія особистісно розвивального навчання «Кола ідей»

Учні об’єднуються у 2 групи. Групи отримують  завдання. Спочатку протягом 2 хвилин учні обговорюють задачу, потім група, яка перша знайшла шлях розв’язання вигукує «Ідея!» і пропонує свій спосіб розв’язування задачі. Ідея обговорюється, коментується і, можливо, доповнюється. Задача розв’язується на дошці.

СЛАЙД 16      Розв’язуваннязадач
1 група – На який термін банк надав позику в розмірі 1000грн., якщо , повертаючи кредит, позичальник сплатив 1875грн., а річна такса становила 25%?

Розв’язання: Оскільки в даному випадку річна такса розраховується з початкового капіталу (позиченої суми), то тут маємо справу з простими відсотками.

За умовою: А_n=1875,    А₀=1000,  =25% . Підставляючи ці дані у формулу A_n=А₀(1+ ), маємо:      1875=1000(1+ ). Звідси 1875=1000+250n, 250n=875,  n=3,5.  Відповідь: 3,5 роки

2 група – У банк, що виплачує 16% річних, покладено 6000 грн. В яку суму перетвориться  цей вклад через 2 роки?

Розв’язання: Відсоткові гроші за перший рік становитимуть:

6000/100*16=960 (грн.). Нарощений капітал через рік становитиме:

6000+6000*0,16=6000(1+0,16)=6000*1,16 (грн.).

Відсоткові гроші за другий рік становитимуть:

6000*1,16/100%*16% (грн.).

Нарощений капітал через два роки становитиме:

6000*1,16+6000*1,16/100%*16%= 6000*1,16(1+0,16)=6000*1,16²=8073,6(грн.)

 

 

СЛАЙД 17                                  Підсумки уроку

Інтерактивна технологія «Незакінчені речення»

• На сьогоднішньому уроці я дізнався(дізналася)...
• На сьогоднішньому уроці найважливішим відкриттям для мене було...
• На початку уроку я поставив(поставила) перед собою ціль. Ось як я її досягнув(досягнула)…

Домашнє завдання

§7, №363(с.р.),369(д.р.), 367(в.р.)