Розробка уроку на тему "Відстані у просторі"

Державний професійно-технічний навчальний заклад

«Ічнянський професійний аграрний ліцей»

 

 

 

 

 

 

 

 

Відкритий урок

 з математики:

 

 

 

«Відстані у просторі»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Підготувала

викладач математики

Яковенко Марина Іванівна

 

 

Тема уроку. Відстані в просторі.

Мета уроку:

-          сформувати в учнів поняття відстані у про­сторі;

-          навчити знаходити відстані у просторі на про­сторових моделях;

-          «читати» геометричні рисунки;

-          повторити матеріал про відстані на площині;

-          розви­вати в учнів логічне мислення;

-          формувати вміння аналізувати, обґрунтовувати відповідь, правильно і лаконічно висловлювати міркування, вміння пра­цювати в групах;

-          виховувати толерантність, ціннісне ставлення до праці.

Тип уроку: засвоєння нових знань і вироблення вмінь.   

Хід уроку

І. Організаційний етап

ІІІ. Формулювання теми, мети і завдань уроку.  Мотивація навчальної діяльності.

Учні записують перші літери слів, які є відповідями на запитання в табличку (Додаток 1) для того, щоб дізнатися тему уроку.

Дешифровщик

ЗАПИТАННЯ:

1.         Частина прямої, що лежить між двома точками (відрізок).

2.         Чорна, червона, кабачкова (ікра).
3.         Хорда, що проходить через центр кола (Діаметр).
4.         Розділ геометрії, який вивчаємо (Стериометрія).
5.         Твердження, що потребує доведення (Теорема).
6.         Твердження, що не потребує доведення (Аксіома).
7.         5-5= (Нуль)
8. Нескінченний десятковий неперіодичний дріб (напиклад П=3,141592…; 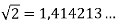; 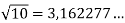) (ірраціональне число)
9.         Навчальне заняття; певний проміжок часу для заняття учнів з окремого предмета. (Урок)
10.    Відрізок, що сполучає дану точку з точкою площини і лежить на прямій перпендикулярній до площини (перпендикуляр).
11.    Результат віднімання (різниця).
12.    Як називаються паралельні сторони трапеції? (Основи)
13.    Відношення протилежного катета до гіпотенузи у прямокутному трикутнику. (синус)
14.    Рівнобедрений . . . (трикутник)
15.    Величина чого-небудь, вимірювана в кубічних одиницях (об’єм )
16.    Чотирикутник, всі сторони якого рівні. (ромб)
17.    Невідома змінна. (ікс)

1    В	2   І	3    Д	4    С	5    Т	6    А	7    Н	8   І
			9    У
10  П	11  Р	12  О	13  С	14  Т	15  О	16  Р	17  І

Надзвичайно важливим є поняття відстані в просторі : між  точками, прямими, площинами, геометричними множинами точок, тілами.

Де нам можуть знадобитися набуті знання в житі? На це запитання ми будемо давати відповідь сьогодні на уроці.

 

IV.Формування знань

Використовуючи листок-трафарет (Додаток 2) та супроводжуючі завдання, учні виконують практичні завдання та повторюють основні поняття по знаходженню відстаней.

• між двома точками
• від точки до прямої
• між паралельними прямими
• від точки до площини

Таким чином йде підготовка до вивчення нового матеріалу на основі узагальнення і повторення вивченого раніше.

Після цього йде  введення нових понять:  означення та знаходження відстаней

• від прямої до паралельної їй площини
• між паралельними площинами
• між мимобіжними прямими

 

Спочатку ми повторимо, розглянувши такі приклади

1. Місяць та Земля, дві точки в просторі. Як нам знайти відстань між ними?

Відстань  між двома́ то́чками —  це довжина  відрізка, кінцями якого є ці точки. Найкоротший шлях, яким можна дістатися з однієї точки в іншу.

 

Давайте виконаємо рисунок та запишемо символьний запис.

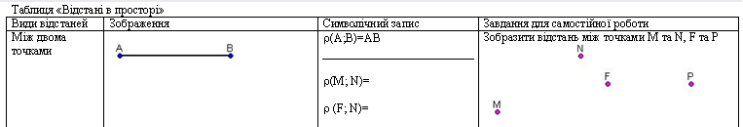
2. Як знайти відстань від годинника до припола (плінтус).

Годинник - це в нас точка, а припіл - пряма.

Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.

 

 

3. Два стовпці паркана - ніби паралельні прямі. Як знайти відстань між ними?

Відстанню між паралельними прямими називається довжина їхнього спільного перпендикуляра. Відстань між непаралельними прямими визначити не можна.

 

 

4. Птаха в польоті над поверхнею землі. Як нам знайти відстань від птахи до землі? Для цього ми повинні знати як знаходити відстань від точки до площини. Птах це точка а поверхня землі це площина.

Відстанню від точки до площини називають довжину перпендикуляра, проведеного з цієї точки до площини.

 

V. Пояснення нового матеріалу.

В ході пояснення виконуються практичні завдання.

Учні записують в зошит формулювання нових теорем (теореми 2, 3 та 4).

Почнемо вивчення нового матеріалу з такого прикладу:

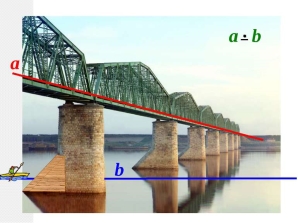
1. Як нам знайти відстань від кабелю електромережі до поверхні землі?

Це приклад математичної задачі на знаходження «відстані від прямої до паралельної площини»

Теорема 2 (про відстань між паралельними прямою і площиною)

Відстань між паралельними прямою і площиною дорівнює довжині спільного перпендикуляра, проведеного з будь-якої точки прямої на площину.

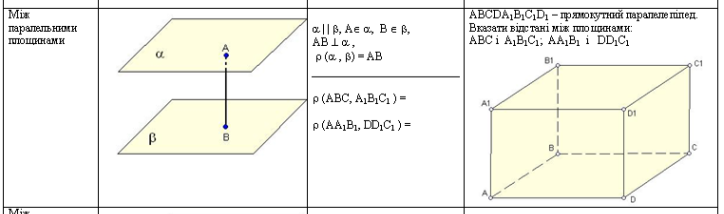
AB ,   B  ,  (A; )=AB

 

2. Як нам правильно виміряти висоту кімнати? Або знайти відстань від стелі до підлоги. Для відповіді на це питання, ми повинні  знати, як знаходять відстань між паралельними площинами.

Теорема 3 (про відстань між паралельними площинами)

Відстань між паралельними площинами дорівнює довжині спільного перпендикуляра, проведеного з будь-якої точки однієї площини на другу.

ǁ,   , B  , AB , (,)=AB

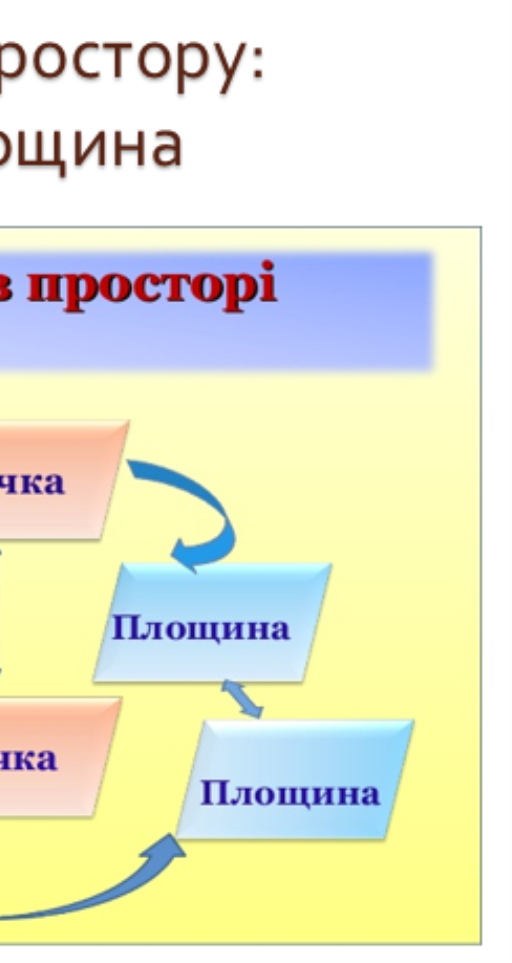
3. Знайти відстань від мосту до річки.

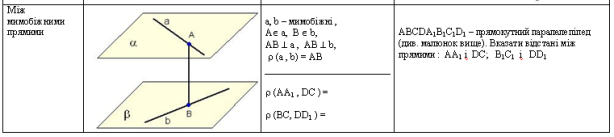
Теорема 4

Дві мимобіжні прямі мають спільний перпендикуляр і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі.

a, b – мимобіжні,   a, B   b, AB a, AB b, (a, b)=AB

 

 

 

 

 

VІ. Розв’язання вправ.

Задача 1

Потрібно протягнути два електричні дроти від стовпа до будинку. На стовпі вони кріпляться на висоті 19 м, а на стіні будинку - 9 м. Скільки потрібно дроту, якщо відстань від стовпа до будинку становить 30 м, а на кріплення і провисання слід додати 5% знайденої довжини.

Розв'язання

Стовп перпендикулярний площині Землі і стіна будинку перпендикулярна площині Землі, отже, оскільки дві прямі, перпендикулярні одній і тій самій площині, паралельні між собою, з цього випливає, що математична модель задачі - прямокутна трапеція.

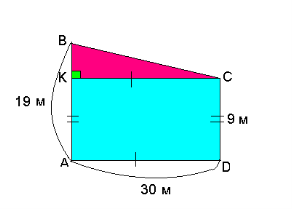
Дано: АВСD-прямокутна трапеція;

           АВ = 19 м, CD = 9 м, AD = 30 м.

Знайти:  ВС.

                       Розв’язання

Опустимо перпендикуляр СК на сторону АВ. АК = CD = 9 м, отже,

ВК = АВ - АК = 19 - 9 = 10 (м).

К С = AD = 30 м.

З Δ ВСК (). За т.Піфагора:

ВС ===(м)

1) 10∙2 = 20(м) - довжина 2-х дротів.

2) 20∙0,05 =(м) - на провисання.

3) 20= 21(м)

Відповідь: необхідно 21м дроту.

 

Задача 2

Чотирисхилий дах будинку квадратної форми зі стороною 16м, має висоту 6м. Скільки квадратних метрів дахового заліза піде на покриття, якщо витрати на згин і обрізки становлять 6%?

 

 

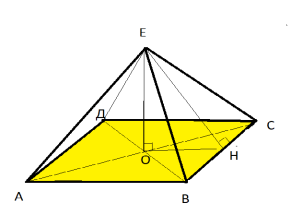
Дано: АВСD-квадрат; ЕО ┴ (АВС)∆

           АВ = 16 м, ЕО = 6 м.

Знайти:  S_{покриття}.

                       Розв’язання

Оскільки т.Е рівновіддалена від сторін АВСD, то т.О – центр вписаного кола ( точка перетину діагоналей). Якщо ЕН ┴ ВС, то за оберненою теоремою про три перпендикуляри ОН ┴ ВС.

S_{покриття}=4 S_∆ВЕС+6

S_∆ВЕС=(ЕН×ВС)÷2

Розглянемо ∆ EOН (<O=90⁰), за теоремою Піфагора EН²= EO² + ОН².

ОН=АВ÷2; ОН=16÷2=8(м);

ЕН²= 6²+8²=36+64=100; ЕН==10(м)

S_∆ВЕС=(10×16)÷2=80 (м²)

4S_∆ВЕС=4×80=320 (м²)

320÷100×6=19.2(м²) 6 від 320

S_{покриття}=320+19.2=339.2 (м²)

Відповідь: 339,2 м2.

 

 

VІI. Підбиття підсумків уроку.

Прийом «Закінчити речення» (усно)

—                  Відстань між двома точками — це...

—                  Відстань між точки до прямої — це...

—                  Відстань між паралельними прямими – це...

—                  Відстань між прямою і паралельною їй площи­ною — це...

—                  Відстань між паралельними площинами — це...

—                  Відстань між мимобіжними прямими — це...

VIII. Домашнє завдання.

Опрацювати §32, виконати №114

Додаток 1

Дешифровщик

ЗАПИТАННЯ:

1. Частина прямої, що лежить між двома точками.
2. Чорна, червона, кабачкова.
3. Хорда, що проходить через центр кола.
4. Розділ геометрії, який вивчаємо.
5. Твердження, що потребує доведення.
6. Твердження, що не потребує доведення.
7. 5-5=
8. Нескінченний десятковий неперіодичний дріб (напиклад П=3,141592…; ; )
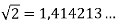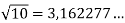9. Навчальне заняття; певний проміжок часу для заняття учнів з окремого предмета.
10. Відрізок, що сполучає дану точку з точкою площини і лежить на прямій перпендикулярній до площини.
11. Результат віднімання.
12. Як називаються паралельні сторони трапеції?
13. Відношення протилежного катета до гіпотенузи у прямокутному трикутнику.
14. Рівнобедрений . . .
15. Величина чого-небудь, вимірювана в кубічних одиницях
16. Чотирикутник, всі сторони якого рівні.
17. Невідома змінна.

1	2	3	4	5	6	7	8
			9
10	11	12	13	14	15	16	17

 

 

Додаток 1

Дешифровщик

ЗАПИТАННЯ:

18. Частина прямої, що лежить між двома точками.
19. Чорна, червона, кабачкова.
20. Хорда, що проходить через центр кола.
21. Розділ геометрії, який вивчаємо.
22. Твердження, що потребує доведення.
23. Твердження, що не потребує доведення.
24. 5-5=
25. Нескінченний десятковий неперіодичний дріб (напиклад П=3,141592…; ; )
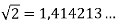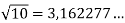26. Навчальне заняття; певний проміжок часу для заняття учнів з окремого предмета.
27. Відрізок, що сполучає дану точку з точкою площини і лежить на прямій перпендикулярній до площини.
28. Результат віднімання.
29. Як називаються паралельні сторони трапеції?
30. Відношення протилежного катета до гіпотенузи у прямокутному трикутнику.
31. Рівнобедрений . . .
32. Величина чого-небудь, вимірювана в кубічних одиницях
33. Чотирикутник, всі сторони якого рівні.
34. Невідома змінна.

1	2	3	4	5	6	7	8
			9
10	11	12	13	14	15	16	17

 

233333куууууууі