Тема уроку.   Ознака паралельності прямих.

Мета уроку: вивчення ознаки паралельності прямих, формування умінь застосовувати ознаку паралельності до розв'язування задач.

Обладнання: моделі прямокутного паралелепіпеда і куба.

Хід уроку

І. Перевірка домашнього завдання

1. Два учні відтворюють розв'язання задач № 5 (1, 3) та 7 (1, 3).

2. Проведення тесту на визначення істинності математичних тверджень.

Тест

У просторі дано дві різні прямі а і b, які:

варіант 1 — лежать в деякій площині;

варіант 2 — не лежать в одній площині.

Позначте символом «+» правильні твердження, символом «-» — неправильні.

1) Прямі α і b можуть перетинатися.

2) Прямі a і b можуть бути паралельними.

3) Прямі a і b можуть бути мимобіжними.

4) Через пряму a обов'язково можна провести площину, яка перети­нає пряму b.

5) Існує деяка пряма с, яка перетинає як пряму а, так і пряму b.

6) Обов'язково існує пряма с, яка перетинає пряму α і паралельна прямій b.

Відповідь.  Варіант 1. 1) +; 2) +; 3) -; 4) -; 5) +; 6) -.

Варіант 2. 1) -; 2) -; 3) +; 4) +; 5) +; 6) +.

II. Сприйняття й усвідомлення нового матеріалу

Ознака паралельності прямих

Як довести паралельність двох прямих на площині? Можна скористати­ся означенням або ознаками паралельності, тобто теоремами, які дають до­статні умови паралельності. Ви вивчали три ознаки паралельності прямих на площині: за рівністю між собою внутрішніх різносторонніх кутів між двома прямими і січною, за рівністю суми внутрішніх односторонніх кутів 180°, а також теорему, що дві прямі, які паралельні третій, паралельні між собою. Перші дві ознаки паралельності не мають аналогів для прямих у просторі. Остання ознака справедлива і в стереометрії. Сформулюємо її.

Теорема.

Дві прямі, паралельні третій прямій, паралельні між собою.

Доведення теореми можна провести так, як це зроблено в підручни­ку, причому теорему вчитель спочатку доводить сам, а потім повторює доведення з учнями, звертаючи увагу на такі питання: чому площини β і γ різні? Чому точка В не лежить на прямій с? Чому площина γ; перетинає площину β, а не пристає до β ?

Можна довести теорему 2.2 іншим способом. Наведемо його.

Доведення

Нехай b║a, с║а. Доведемо, що b║с .

Прямі b і с не можуть перетинатися. Інакше через точку їх перетину проходили б дві різні прямі, паралельні прямій а, що суперечило б тео­ремі 2.1.

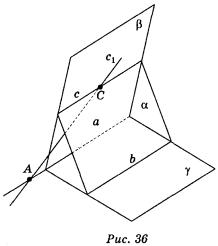
Припустимо, що прямі b і с — мимобіжні (рис. 36). Через паралель­ні прямі b і а, с і a проведемо площи­ни γ і β, а через пряму b і точку С прямої с — площину α. Нехай площини α і β перетинаються по пря­мій c₁. Прямі а, с, c₁ лежать в одній площині β , причому с║а. Тому пря­ма с₁, яка перетинає с, перетинає пря­му a в деякій точці А. Прямі c₁ і а лежать відповідно у площинах α і γ , тому їх спільна точка А належить цим площинам, а отже, і їх спільній пря­мій b. З припущення випливає, що паралельні прямі a і b мають спільну точку А, що суперечить умові.

Отже, прямі b і с не можуть ні перетинатися, ні бути мимобіжни­ми. Таким чином, b║с .

Виконання вправ

1. Дано зображення куба ABCDA₁B₁C₁D₁. Доведіть, що;

а) АА₁ || СС₁;   б) АВ || C₁D₁;   в) AC || А₁С₁.

2. Чи правильне твердження: якщо прямі b і с не паралельні одній і тій самій прямій а, то b і с не паралельні між собою?

3. ABCDA₁B₁C₁D₁ — паралелепіпед. Доведіть, що площина АСС₁ про­ходить через точку А,.

4. Прямі а і b паралельні, а прямі b і с не паралельні. Доведіть, що прямі а і с не паралельні.

III. Закріплення та осмислення знань учнів

Розв'язування задач

1. Трикутник АВС і трапеція ABED (АВ — основа) не лежать в одній площині. Точки Μ і N — середини сторін АС і ВС відповідно. Дове­діть, що ΜΝ || DE .

2. Задача № 11 із підручника (с. 19).

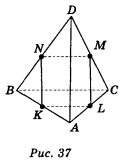3. Точки К, L, Μ, Ν — середини ребер АВ, АС, CD, DB тетраедра, всі ребра якого рівні. Знайдіть довжину ребра тетраедра, якщо пе­риметр утвореного чотирикутника KLMN до­рівнює 4a (рис. 37).

4. Задача № 12* (с. 19).

IV. Домашнє завдання

§ 1, п. 8; контрольне запитання № 4; задачі № 9, 10 (с. 19).

V. Підведення підсумку уроку

Запитання до класу

1) Сформулюйте ознаки паралельності прямих на площині.

2) Сформулюйте ознаки паралельності прямих у просторі.