Розробка уроку "Найбільше і найменше значення функції"

Розробка уроку викладача математики і фізики ПАЛ с. Веприк Гадяцького району Полтавської області

Найбільше і найменше значення  функції

Мета: - навчити учнів  правил знаходження найбільшого і найменшого значення функції;

  -   навчити застосовувати ці правила під час розв’язування завдань;

 -   розвинути логічне мислення;

  -   виховати почуття  відповідальності.

 

Тип уроку: урок вивчення нової теми.

Обладнання: ноутбук ‚ проектор, таблиця

 

 План уроку  

1.Організаційний момент(1хв.)

2. Актуалізація опорних знань(10 хв.)

3.Вивчення нової теми(15 хв.)

4.Закріплення вивченого матеріалу(15 хв.)

5.  Підсумок уроку. Домашнє завдання(4 хв.)

Хід уроку

1. Організаційний момент.

Перевірка відсутніх.

Сьогодні на уроці ми з вами вивчимо правила знаходження найбільшого і найменшого значення функції‚ а також навчимося застосовувати їх при розв’язуванні завдань.

 У вас на столі лежать листочки зеленого ‚ жовтого кольорів. В кінці уроку кожен з вас вибере листочок ‚ який відповідає його рівню засвоєння матеріалу і повісить його на дерево (гілочку).  Якщо ви виберете зелений колір –  засвоїли матеріал ‚ жовтий колір -  частково засвоїли матеріал. Тому будьте уважні ‚ активні ‚ щоб наше дерево в кінці уроку було зеленим без жодного жовтого листочка.

2.Актуалізація опорних знань.

Проведемо інтерактивну гру «Так чи ні»(називаю функцію і її похідну, а ви повинні сказати так – якщо правильна відповідь і ні –  якщо не правильна )

1		У=2	У ′ =0
2		У=2х	У ′ =2
3		У=5,5х	У ′ =5,5
4		У=х2	У ′ =2х
5	У=2х2		У ′ =6х2
6	У=х4		У ′ =х2
7	У=х3+2		У ′ =3х2
8	У=sinx		У ′ =

 

А зараз перевіримо ваші знання з теми «Похідна» і розгадаємо тему нашого уроку. Для цього кожен учень розв’язує завдання, а навпроти відповіді записана буква. Номер завдання відповідає номеру букви у слові.(на слайді №1заздалегідь написані квадратики в які потрібно вписати букви; кожен учень розв’язує по одному завданні. Але якщо учнів менша кількість ніж букв в слові то деякі учні розв’язують по два приклади)

1	У=х4+2	У ′ =4х3	Н
2	У=2х3	У ′ =6х2	А
3	У=0,5х-1	У ′ =25х4	Б
4	У=5х5+5	У ′ =cosx	І
5	У=sinx	У ′ =	Е
6	Y=cosx	У ′ =1	І
7	Y=tgx	У ′ =-sinx	Л
8	Y=ctgx	У ′ =	Ь
9	Y=	У ′ =0,5	Й
10	Y=x	У ′ =	Ш
11	Y=lnx	У ′ =9х2+1	Й
12	Y=	У ′ =0	М
13	У=3х3+х	У ′ =	Н
14	У=7	У ′=18х	Е
15	У=9х2-6	У ′=	Ш
16	У=2	У ′=40x9	Е
17	У=logax	У ′=5cosx	З
18	У=4x10+5	У ′=	Н
19	У=5sinx	У ′=sinx	Н
20	У=	У ′=	А
21	У=12tgx	У ′=3cos3x	Е
22	У=7ctgx	У ′=	Н
23	У=sin3x	У ′=3+26x	Н
24	У=cos	У ′=25+5x4	Я
25	У=3x+13x2	У ′=	Ф
26	У=25x+x5	У ′=	У
27	У=10lnx	У ′=cosx+sinx	К
28	У= 6log6 x	У ′=	Н
29	У=log5x	У ′=8ex	Ц
30	У=sinx – cosx	У ′=9x8+8x7	І
31	У=8ex	У ′=2	Ї
32	У=x9+x8	У ′=	А
33	У=1+2x+0,6	У ′=	Ч

3.Вивчення нової теми.

        Отже ми розгадали тему уроку і повторили вивчений матеріал. Записуємо тему уроку в зошити і все ‚ що буде записано на дошці чи на слайдах під час уроку . Якщо комусь щось буде не зрозуміло ‚ то запитуйте одразу .

Нехай на відрізку [a;b] задана неперервна функція y=f(x). Тоді, як доводиться в курсі математичного аналізу, серед множини значень такої функції є найбільше і найменше значення. Ці числа і називаються відповідно найбільшим і найменшим значенням функції. Постає запитання: як знайти точки відрізка[a;b], в яких функція набуває свого найбільшого і найменшого значень?

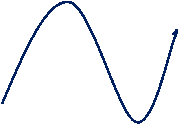
Зазначу, що функція може набувати свого найбільшого і найменшого значень як на кінцях відрізка, так і у внутрішніх його точках. Наприклад, на мал.1 зображено графік неперервної функції, яка у внутрішній точці с₁ відрізка [a;b] набуває найбільшого значення, а у внутрішній точці с₂ – найменшого. Слайд №2

      у

 мал.1

 

 

0 

a           с₁             с₂b                    х

На мал.2  зображено графік функції, яка на кінцях відрізка набуває найменшого і найбільшого значень. Слайд №3

 

 

 

 

y                                                                                             мал.2

 

 

 

 

0                abx

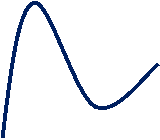
Може статися і так, що одного із значень функція набуває всередині відрізка, а другого – на одному з кінців. Так, на мал.3 зображено графік неперервної функції, яка на лівому кінці відрізка(точка а) набуває найменшого значення, а у внутрішній точці(точці с) –найбільшого. Слайд №4

 

 

y

 

Мал.3

 

 

 

0         acbx

Якщо функція набуває найбільшого(найменшого ) значення всередині відрізка, то це найбільше(найменше) значення є одночасно і локальним максимумом(мінімумом) заданої функції. Звідси випливає правило знаходження точок, в яких функція набуває найбільшого(найменшого) значення на відрізку [a;b].

Щоб знайти найбільше(найменше)значення неперервної функції на відрізку[a;b], треба знайти всі локальні максимуми(мінімуми) і порівняти їх із значеннями функції, яких вона набуває на кінцях відрізка. Найбільше(найменше) число серед утворених чисел і буде найбільшим(найменшим) значенням функції, заданої на відрізку [a;b]. Слайд №5

А зараз розв’яжемо завдання, застосовуючи правила знаходження найбільшого і найменшого значення функції. Слайд №6,7

У=2х³+3х²-12х +7, х є[0;2].

Знаходимо похідну за правилами знаходження похідних, які ми з вами повторили на початку уроку.

у^′=6х²+6х-12.

Прирівняємо похідну до нуля і знайдемо стаціонарні точки.

6х²+6х-12=0

Скоротимо на 6. Отримаємо х²+х-2=0

Знайдемо корені рівняння за теоремою Вієта х₁+х₂=;  х₁х₂=; отже, х₁=1; х₂=-2. Перевіримо, чи належать наші точки відрізку[0;2]. 1є[0;2], а -2є  [0;2]. Обчислимо значення функції в точці х₂=1 і на кінцях відрізка, тобто в точках х₃=0; х₄=2.

У(2)=2∙2³+3∙2²-12∙2+7=16+12-24+7=11;

У(1)=2∙1³+3∙1²-12∙1+7=2+3-12+7=0;

У(3)=2∙0³+3∙0²-12∙0+7=7.

Отже найбільше значення дорівнюєy=y(2)=11; найменше значення функції y=y(1)=0.

Розглянемо практичне застосування знаходження найбільшого і найменшого значення функції. Слайд №8,9

Якими мають бути сторони прямокутної ділянки площею1600 м², якщо на її огорожу витрачено найменшу кількість матеріалу?

Нехай одна сторона прямокутника х м, тоді друга м, а периметр Р(х)=2(х+)м. Найменша кількість матеріалу  витрачається при найменшому периметрі. Знайдемо похідну функції Р(х) і прирівняємо її до нуля: Р(х)=2(1-)=; ; 0; 2(х²-1600)=0; 2х²=3600; х²=1600; х=40; х0, тому х=40. Відповідь: 40м, 40м.

4.Закріплення вивченого матеріалу.

А тепер розв’яжемо завдання на дошці(2 учні), а решта працюють в зошитах самостійно і перевіряють розв’язки на дошці. Слайд№10

1.Знайти довжину сторін прямокутника, що має площу 144м² та найменший периметр.

Нехай одна сторона прямокутника х см, тоді друга - см, а периметр Р(х)=(2х+2∙) см. Знайдемо похідну і прирівняємо до нуля.

Р(х)= 2+2∙(-)=2-; 2-=0;2х²=288; х²=144; х=12;х0; х=12. Відповідь: 12 см; 12 см.

2.Знайти найбільше і найменше значення функції  f(x)=x³-3x, на відрізку 

х є[0;2]

f′(x)=3х²-3;3х²-3=0; 3х²=3; х²=1; х=1; -1не належить [0;2]

f(0)=0³-3∙0=0

f(1)=1³-3∙1=-2

f(2)=2³-3∙2=2

Отже найбільше значення дорівнюєf=f(2)=2; найменше значення функції f=f(1)=-2.

А тепер розгадаємо  вислів Ч.Діккенса.(Немає у світі такої височини, верхівки якої не зможе досягнути наполегливість)

Робота в парах.  Кожній парі учнів  роздаю картки із завданнями, розв’язавши які учень розгадує номер квадратика на який потрібно причепити картку зворотним боком.(на дошці висить ватман, який розбито на квадрати) Якщо всі учні розв’яжуть правильно, то розгадаємо вислів.  Хто ж зробить помилку – учень недостатньо засвоїв матеріал. Йому потрібно підійти після уроків на додаткове заняття і оцінка за урок буде нижчою.

 1.Знайти найбільше і найменше значення функції У=2х²+4х на [0;2]

 у′=4х+4, 4х+4=0, 4х=-4, х=-1; у(0)=0; у(2)=16.

А)Найбільше значення функції у(2)=16.

Найменше значення функції у(0)=0; №1

Б))Найбільше значення функції у(2)=16.

Найменше значення функції у(0)=0;№3

2.Знайти найбільше і найменше значення функції У=2х² на [0;2]

у′=4х, 4х=0,  х=0; у(0)=0; у(2)=8. 

А)Найбільше значення функції у(2)=8.

Найменше значення функції у(0)=0; №3

Б))Найбільше значення функції у(2)=16.

Найменше значення функції у(0)=0;№3

3.Знайти найбільше і найменше значення функції У=х² +2х на [-1;2]

у′=2х+2, 2х+2=0,  х=-1; у(-1)=-1; у(2)=8.

А)Найбільше значення функції у(2)=8.

Найменше значення функції у(-1)=-1; №2

Б))Найбільше значення функції у(2)=16.

Найменше значення функції у(0)=0;№3

4.Знайти найбільше і найменше значення функції У=х³ +3х на [-1;3]

у′=3х²+3; 3х²+3=0,  х=1; у(-1)=-4; у(3)=36, у(1)=4

А)Найбільше значення функції у(2)=8.

Найменше значення функції у(-1)=-1; №2

Б))Найбільше значення функції у(3)=36.

Найменше значення функції у(-1)=-4;№5

5.Знайти найбільше і найменше значення функції У=х⁴ +4х на [-1;1]

у′=4х³+4; 4х³+4=0,  х=-1; у(-1)=-3; у(1)=5.

А)Найбільше значення функції у(2)=8.

Найменше значення функції у(-1)=-1; №2

Б))Найбільше значення функції у(1)=5;

Найменше значення функції у(-1)=-3;№4.

6.Знайти найбільше і найменше значення функції У=3х⁵  на [-1;1]

у′=15х⁴; 15х⁴=0,  х=0; у(0)=0; у(1)=3; у(-1)=-3.

А)Найбільше значення функції у(1)=3.

Найменше значення функції у(-1)=-3; №7

Б))Найбільше значення функції у(1)=5;

Найменше значення функції у(-1)=-3;№4.

7.Знайти найбільше і найменше значення функції У=6х-3х² на [-1;1]

у′=6-6х; 6-6х=0,  х=1;  у(1)=3; у(-1)=-9.

А)Найбільше значення функції у(1)=3.

Найменше значення функції у(-1)=-3; №7

Б))Найбільше значення функції у(1)=3;

Найменше значення функції у(-1)=-9;№6

8.Знайти найбільше і найменше значення функції У=5-7х²  на [-1;3]

у′=-14х; -14х=0,  х=0; у(0)=5; у(3)=-58; у(-1)=-2.

А)Найбільше значення функції у(0)=5.

Найменше значення функції у(3)=-58; №8

Б))Найбільше значення функції у(1)=5;

Найменше значення функції у(-1)=-3;№4.

5.Підсумок уроку. Домашнє завдання.

Отже, який можна зробити висновок? Лише завдяки вашій наполегливості можна вивчити програмовий матеріал і отримати хороші оцінки.

Інтерактивна вправа «Закінчи речення»

-я зрозумів…

- я дізнався…

- я не зрозумів…

-я хотів би дізнатися…

Запишіть домашнє завдання.(слайд №11)

1.Вивчити Розв’язати №3(а), №4(б).

2.Скласти кросворд за темою «Похідна».

3.Придумати рекламу, у якій говориться про важливість уміння розв’язувати завдання на знаходження найбільшого і найменшого значення функції. Оголошую оцінки за урок, аргументую їх. Потім кожен учень вибирає листочок того кольору, який йому більше імпонує – тобто засвоєнню чи незасвоєнню матеріалу з теми «Найбільше і найменше значення функції».