Державний навчальний заклад

 «Одеський центр професійно-технічної освіти»

Методична розробка уроку з предмету: «Геометрія»

Тема уроку: «Піраміда. Правильна піраміда»

Виконавець 

Викладач інформатики і математики

Башкатова Є.В.

Розглянуто та погоджено на засіданні методичного об’єднання викладачів базових предметів

 та рекомендовано до використання  в навчально-виховному процесі

Протокол №___ від «___» ___ 20___р. Голова МО ________ Гачук О.В.

                                                               Овідіополь

Зміст:

1.    Анотація………………………………………………………..2

2.    Вступ…………………………………………………………...3

3.    Конспект уроку «Піраміда. Правильна піраміда»……………5

4.    Висновок………………………………………………………15

5.    Список використаних джерел………………………………..17

6.    Додатки…………………………………………………….......18

Анотація

         Кожен викладач прагне зацікавити здобувачів освіти предметом, який він викладає, бо це є запорукою успішного навчання. Вміло організована робота сприяє вихованню здобувачів освіти, розширює і поглиблює здобуті на уроках знання, а також сприяє зацікавленню предметом.

      Методична розробка уроку з геометрії «Піраміда. Правильна піраміда» призначена для проведення заняття в учнів другого курсу під час вивчення теми  «Многогранники».

       Мета уроку «Піраміда. Правильна піраміда» - це: сформувати поняття піраміди, правильної піраміди, елементи піраміди; домогтися засвоєння властивостей правильної піраміди. Сформувати вміння розв'язувати задачі на знаходження елементів правильної піраміди. 

      Данна розробка уроку містить: теоретичний матеріал, завдання для розв’язання; практичний матеріал для закріплення теоретичного матеріалу у вигляді графічного диктанту; інтерактивного завдання,  кросворд «Многогранники». Також при проведенні уроку застосовані методи навчання: метод «мозговий штурм», словесні – бесіда, пояснення; демонстрація презентації, спостереження здобувачів освіти,групова робота.

    Даний урок розроблено мною із використанням такого виду інноваційної технології, як предметно – зорієнтований, використавши один із елементів технології, а саме ігрову з використанням інтерактивних завдань.. Я прагнула створитиумови для повного індивідуального розвитку здобувача освіти, актуалізацію його можливостей. Хочу навести слова Венера “Якщо ми хочемо, щоб дитина щось засвоїла , то потрібно це втілити в діяльність самої дитини”. 

      Ця розробка буде корисна всім викладачам математики  у вивчені різних галузях.

Вступ.

         Основним підходом до організації системи навчання в сучасному закладі освіти залишається поурочна система, за якої провідною формою організації навчальної роботи є урок.

        Уроки мають захоплювати здобувачів освіти, будити в них інтерес та мотивацію, навчати самостійному мисленню та діям. Ефективність і сила впливу на емоції і свідомість учнів значною мірою залежить від умінь та стилю роботи викладача.

      Наука, суспільство змінюються, набувають нові якості, реформи відбуваються у всіх сферах життя нашого суспільства, в тому числі і в освіті. В результаті, поняття сучасного уроку набуває нового змісту. Поняття «сучасний урок» знаходиться в постійній динаміці. Розвиток таких наук, як педагогіка, дидактика, методика, психологія веде до постійного удосконаленню поняття «сучасний урок», так як досягнення цих наук суттєво впливають  і на сам урок. 

     В сучасних умовах відбувається усвідомлення цінності та практичної значущості освіти. У результаті цього значно зростають вимоги до якості освіти здобувачів освіти. Викладач в таких умовах стоїть перед необхідністю удосконалення всіх сторін процесу навчання. Сучасний етап суспільного розвитку характеризується низкою особливостей, які висувають нові вимоги до освіти. Змінюються пріоритети й акценти в освіті, воно стає спрямованим на розвиток особистості, формування в учнів таких якостей і умінь, які в подальшому повинні дозволити йому самостійно вивчати що-небудь, освоювати нові види діяльності і, як наслідок, бути успішним у житті. Мета  роботи - розглянути включення різних методів і технологій в урок математики щоб він відповідав поняттю «сучасний урок математики», показати на прикладі  уроку можливість включати нестандартні методи в структуру уроку.

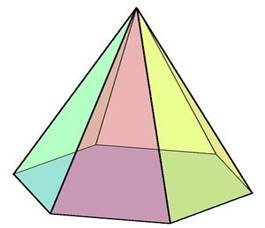
Розгорнутий конспект уроку

Епіграф до  уроку:             “Знання можуть бути купоюкаміння,                    що задавила особистість.

                 І знання можуть бути вершиною піраміди,                          на якій стоїть особистість.”

Мета: навчальна – сформувати поняття піраміди, правильної піраміди, апофеми правильної піраміди, елементи піраміди; домогтися засвоєння властивостей правильної піраміди. Сформувати вміння розв'язувати задачі на знаходження елементів правильної піраміди.  розвивальна – розвивати графічну культуру учнів, просторову уяву, розширювати знання математичної термінології. виховна – виховувати культуру математичної мови, зібраність, охайність, інтерес до математики.

Тип уроку: урок засвоєння нових знань, формування вмінь і навичок.

Основні поняття. Піраміда, правильна піраміда, апофема правильної піраміди.

Обладнання: Підручник за редакцією Г.П. Бевз, В.Г. Бевз, презентація «Піраміда.Правильна піраміда», моделі  пірамід, мультимедійні засоби.

Міжпредметні зв’язки. Фізика, географія, художня культура.

Очікувані результати: після уроку здобувачі освіти зможуть:

•      вирізняти піраміди серед многогранників та правильні піраміди серед інших пірамід;

•      будувати  піраміди та знаходити їх елементи;

•      розв'язувати задачі з використанням властивостей  піраміди.

Зміст уроку

1.Організаційний момент…………..2хв

2.   Актуалізація опорних знань…….6хв 

3.   Мотивація навчальної діяльності………3хв

4.   Вивчення нового матеріалу……….20хв

5.   Систематизація і узагальнення знань……10хв

6.   Підведення підсумків заняття……….3хв

7.   Домашнє завдання……..1хв

ХІД УРОКУ:

1. Організаційний момент. 

Привітання викладача: Добрий день! Усміхніться один одному, подумки побажайте успіхів на цілий день. Для того, щоб впоратися на уроці з завданнями, будьте старанними і уважними. Завдання наші такі: 

Не просто слухати, а чути.

Не просто дивитися, а бачити.

Не просто відповідати, а міркувати. Дружно і плідно працювати.

–   перевірка наявності здобувачів освіти;

–   перевірка готовності здобувачів освіти до уроку.

2.   Актуалізація опорних знань (робота з групою усно):

Викладач: Спробуємо пригадати(використання моделей  геометричних тіл ( різні призми та піраміди) .

-       як називаються моделі , що лежить на моєму столі? ( Очікувана відповідь многогранники);

-       а якщо додати цилиндр та конус (Очікувана відповідь тіла);

-       що таке многогранник? (Очікувана відповідь многогранник - це таке тіло, поверхня якого складається з кінцевого числа плоских многокутників);

-       розділіть многогранники на дві групи (Очікувана відповідь призми - піраміди);

-       які многогранники ми вивчали? (Очікувана відповідь призми);

-       що таке призма? (Очікувана відповідь призмою називається многогранник, який складається з двох плоских многокутників, які лежать в різних площинах і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих многокутників);

-       вкажіть її елементи (Очікувана відповідь основи, бічні ребра, вершини, висота, грані, діагоналі);

-       дайте означення елементів  та покажіть на моделях;

-       як називаються ці тіла? (Очікувана відповідь піраміди);

-       і так тема уроку «Піраміда. Правильна піраміда.» 

3.   Мотивація навчальної діяльності. Історичний екскурс.

Для сьогоднішнього уроку я підібрала вислів:

“Знання можуть бути купою каміння,                    що задавила особистість.

        І знання можуть бути вершиною піраміди, 

                                                        на якій стоїть особистість.” 

Я вам бажаю, щоб ваші знання стали вершиною.

У когось це слово асоціюється з Єгипетськими пірамідами , але монументальні споруди створені людиною зустрічаються і в Центральній Америці, на острові Тенеріфе, на тілі гімалайського хребта виділяється пірамідальне плато, створене природою;

пірамідальна форма широко використовується в архітектурі, наприклад у Франції, в Німеччині

Слово «піраміда» - латинська форма грецького слова «пюрамис», так греки називали єгипетські піраміди, походить від давньоєгипетського слова «пурамі» (так називали піраміди єгиптяни). Єгипетські піраміди – перше з 7 чудес світу. Єгипетська гробниця Хеопса – найбільша з пірамід. Вона була побудована приблизно 6000 років тому фараоном Хеопсом. Підраховано, що піраміда складається з 23 000 000 обтесаних вапнякових каменів вагою 2,5 тонни кожен. Загальна вага піраміди 5 750 000 тонн. Висота піраміди приблизно 140 метрів. Що б обійти піраміду кругом, треба пройти цілий кілометр. Припускають, що піраміду будували 20 років 100 тисяч рабів, змінюються кожні три місяці. Підраховано, що з каменів гробниці Хеопса можна було побудувати сучасне місто з населенням в 120 тисяч чоловік. 

4. Вивчення нового матеріалу.

Викладач: Зараз ми з вами розглянемо піраміду з математичної точки зору.

-  Що ми можемо дізнатися про піраміду? познайомитися з поняттям піраміда, видами,  її елементами, властивостями, розв’язувати  найпростіші завдання;

-  Отже, мета уроку вивчити піраміду і її елементи та що таке правильна піраміда;

-  Де нам це може знадобитися? (Очікувана відповідь при розв’язанні завдань, в різних галузях);

-  Сформулюємо означення  піраміди 

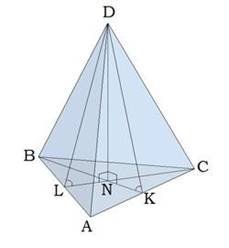
ОЗНАЧЕННЯ.ПІРАМІДОЮ НАЗИВАЄТЬСЯ  МНОГОГРАННИК,  

                           ЩО СКЛАДАЄТЬСЯ З  

ПЛОСКОГО МНОГОКУТНИКА – ОСНОВИ  ПІРАМІДИ,  

ТОЧКИ, ЯКА НЕ НАЛЕЖИТЬ ПЛОЩИНІ  ОСНОВИ – ВЕРШИНИ ПІРАМІДИ,  

ТА ВСІХ ВІДРІЗКІВ, ЩО СПОЛУЧАЮТЬ ВЕРШИНУ ПІРАМІДИ З                       

ТОЧКАМИ ОСНОВИ.

 - давайте визначимо основні елементи піраміди 

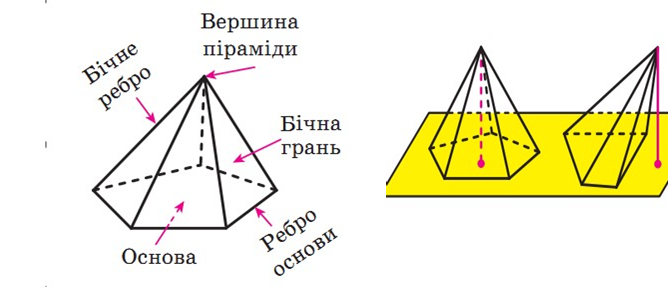
Це є - основа, вершина, бічні ребра - відрізки, що сполучають вершину піраміди з вершинами основи,  висота - перпендикуляр, опущений з вершини піраміди на площину основи

      Поверхня піраміди складається з  основи  і бічних граней – трикутники.

     У чому полягає відмінність пірамід? Вона полягає в тому, що в основі лежать  різні многокутники.Наприклад, якщо в основі - трикутник, то це трикутна піраміда, чотирикутник - чотирикутна і т. д. Тобто, вид піраміди залежить від многокутника, який лежить в основі.

      Розглянемо означення правильної піраміди.

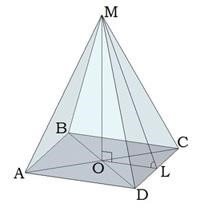
ОЗНАЧЕННЯ 1. Піраміда, в основі якої лежить правильний многокутник і всі бічні ребра рівні між собою, називається правильною.

ОЗНАЧЕННЯ 2. Піраміда, в основі якої лежить правильний многокутник і основа висоти піраміди збігається з центром цього многокутника,                     називається правильною.

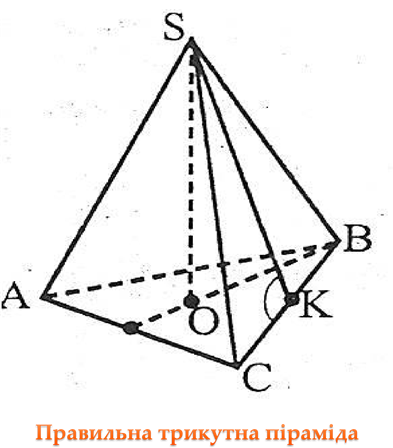
Одним із прикладів правильної піраміди є єгипетські піраміди. Це чотирикутні піраміди.

Алгоритм побудови правильної піраміди:

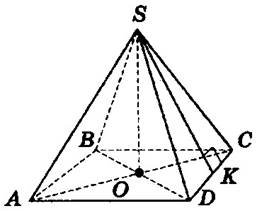-    малюється основа;

-    знаходиться проекція вершини на площину основи;

-    вертикально проводиться висота;  проводяться ребра.

Сформулюємо властивості правильної піраміди: 

1)  усі бічні ребра правильної піраміди рівні;

2)  усі бічні грані правильної піраміди  рівні рівнобедрені трикутники;

3)  усі апофеми правильної піраміди рівні між собою;

4)  двогранні кути при основі рівні; 

5)  двогранні кути при бічних ребрах рівні; 

6)  кожна точка висоти правильної піраміди рівновіддалена від всіх вершин основи; 

7)  кожна точка висоти правильної піраміди рівновіддалена від усіх бічних граней.

Зверніть увагу!

Неправильні піраміди апофеми не мають. 

Піраміда у якої всі бічні грані є правильні трикутники називається тетраедром.

Бічна поверхня піраміди складається з усіх бічних граней.

Розглянемо що таке апофема в правильної піраміді. 

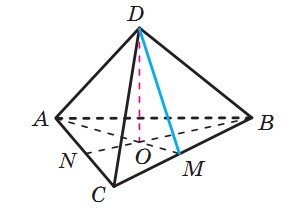DO- апофема

Апофема – висота бічної грані правильної піраміди, проведена з її вершини. Цей термін вживається тільки для правильної піраміди, хоча у неправильної піраміди також можуть бути рівні висоти бічних граней.

Отже, ми розглянули означення  піраміди, її елементи, властивості.

 Розв’язання задачі. 

Задача. В основі піраміди  Хеопса – квадрат зі стороною  230м, висота -  138 м. Знайти бічне ребро, апофему , площі поверхонь та об'єм   самої  високої египетської піраміди .

Розв’язання 

Апофема 138 115 179  r115

                   Бічне ребро 138                     213, R

S_b  0.5Po*l  05*4*230*179  82340

Sp  0.5Po*l a²  05*4*230*179  230²  82340 52900 

135240

V 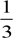S*H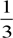52900*1382433400

5.   Систематизація і узагальнення знань. 

З метою перевірки засвоєння учнями теоретичного матеріалу з учнями проводиться графічний диктант.

Правильна відповідь Неправильна відповідь Чи правильно, що:

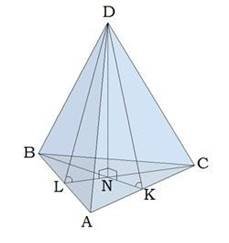
Øякщо бічні ребра піраміди утворюють рівні кути з висотою піраміди, то основою висоти є центр кола, вписаного в піраміду;

Øякщо висоти всіх бічних граней, проведені з вершини піраміди, рівні, то основою висоти є центр кола, вписаного в основу піраміди;

Øякщо бічні ребра піраміди рівні і її основою є тупокутний трикутник, то основа висоти лежить поза основою піраміди;

Øякщо бічні ребра піраміди рівні і її основою є прямокутний трикутник, то основа висоти лежить усередині трикутника;

Øякщо бічні ребра піраміди рівні і її основою є прямокутний трикутник, то основою висоти є середина гіпотенузи трикутника;

Øу піраміди може бути дві бічні грані, які перпендикулярні до основи;

Øу піраміди може бути три бічні грані, які перпендикулярні до основи;

Øякщо одна з бічних граней піраміди перпендикулярна до площини основи, то висота піраміди збігається з висотою цієї грані;

Øякщо всі бічні ребра піраміди рівні, то основою висоти піраміди є центр кола, описаного навколо основи піраміди.

Здобувачі освіти обмінюються зошитами та проводять взаємоперевірку. Після цього обговорюємо питання, при відповіді на які, були допущені помилки.

6.   Підбиття підсумків уроку. 

       Отже, сьогодні на уроці ми розглянули означення  піраміди, означення правильної піраміди, її елементи, властивості. Роблячи висновок про піраміди, можна  сказати що піраміда Хеопса творіння людського генія - це пам’ятник не тільки архітектури, але й математики.

І кожна цегла, статуя, колона,

Мережечка, різьба і малювання Незримим устами промовляє:

«Мене створив Єгипетський народ і Тим на вік своє імення вславить»

Так переклала напис на руїні піраміди Леся Українка.

Я бажаю вам, любі здобувачі освіти, щоб ваші знання і вміння,  як камені Великої Піраміди, як цеглинки складалися один до одного, утворюючи Велику піраміду знань. Щоб вони були такими ж довговічними і кріпкими. І, пам’ятайте, щоб збудувати перше чудо світу, єгиптянам треба було довго і важко працювати. 

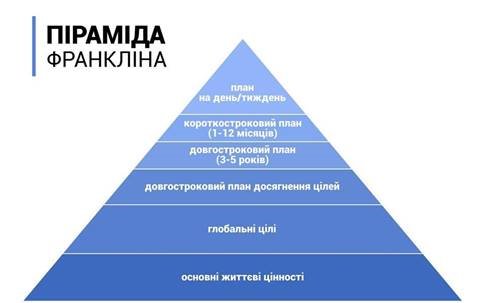
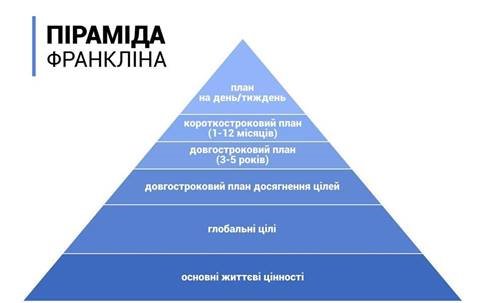
На завершення уроку мені б хотілося продемонструвати піраміду успіху – піраміду Франкліна.

(Викладач оцінює роботу окремих учнів, озвучує і коментує оцінки учнів, які активно працювали протягом уроку, враховуючи усі відповіді.)

7. Домашнє завдання:

1.   Опрацювати новий матеріал.

2.   Інтерактивна вправа ( виконують на телефоні).

https://learningapps.org/display?v=p5zzc6fqt19

Висновок.

Математика ― одна з найдавніших та складних      наук, без     якої немислимий подальший розвиток людства, науці цікавій, захоплюючій, могутній.    Значення математичних знань у нашому житті дійсно важко оцінити. Сучасна техніка ― це перш за все математика в різних її застосуваннях. Ми,

ті хто сьогодні, говоримо: «Математика― всемогутня! Вона зуміла казки зробити дійсністю!

Основними цілями даної розробки є:

-       сформувати означення піраміди її елементів та видів;

-       сформувати вміння розрізняти зображення піраміди серед інших фігур;

-       оволодіти навичками побудови пірамід на площині;

-       розвиватиматематичну культуру здобувачів освіти;

-       розширити і поглибити рамки навчальної програми шляхом міжпредметних

зв’язків;

-       привчати здобувачів освіти користуватися додатковими джерелами інформації, робити висновки і узагальнення;

-       виховувати інтерес до геометрії та історії математики; наполегливість, самостійність, відповідальність та вимогливість до себе.

Тема даного уроку допомагає здобувачам освіти отримати  необхідні навички та знання для розв’язування різноманітних математичних задач, а у подальшому і прикладних задач пов’язаних з пірамідою .

Сучасна освіта повинна застосовувати сучасні методи та форми навчання, які б сприяли максимальній доступності знань, швидкому та надійному їх засвоєнню, підвищували інтерес учнів до предмета, розвивали їх творчий потенціал , навчали отримувати знання з різних інформативних джерел. Тому на уроці застосовуються інтерактивне завдання, презентація.

Отже, застосування комп’ютерних програмних засобів дає змогу вирішити проблему більш якісного засвоєння знань з геометрії  та здатності їх застосування на практиці, підвищує математичну грамотність здобувачів освіти, сприяє розвитку в них математичної компетентності.

Список використаних джерел.

1.Математика: Підручник Математика: 11 кл : підруч. для загальноосвіт. навч закл : рівень стандарту / Г.П. Бевз, В.Г. Бевз. – 2-ге вид. – К. : Генеза, 2012. 

2.Математика : Алгебра і початки аналізу та геометрія. Рівень стандарту : підруч. для 11 кл. закладів загальної середньої освіти / Г. П. Бевз, В. Г. Бевз. — К. : Видавничий дім «Освіта», 2019. — 272 с. : іл.

3.Погорєлов О. В. Геометрія : Стереометрія : підруч. для 10—11 кл. серед. шк. — 6-те вид. — К. : Освіта, 2001.— 128 с. 

4.Геометрія. 10-11 класи : пробний підручник / О. М. Афанасьєва [та ін.]. — Тернопіль : Навчальна книга — Богдан, 2018. — 264 с. 

5.Михайленко В. Є., Ковальов С. М. та ін. Корисна геометрія : підручник для вузів. — К. : Вища школа,2013. — 134 с.

6.Матеріал з Вікіпедії — вільної енциклопедії.

Додатки.

Додаток 1.

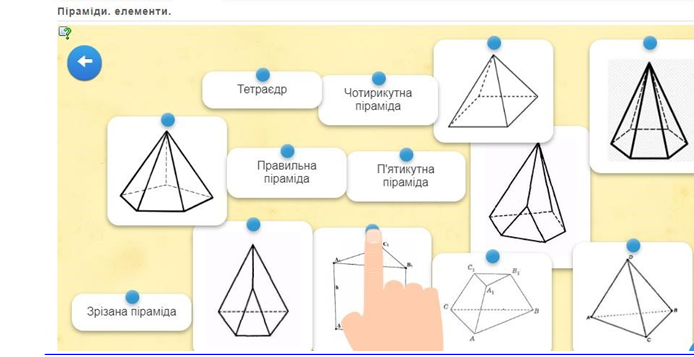
Кросворд « Многогранники»

Додаток 2. Таблиця «Правильні піраміди»

Додаток 3.

Додаток 4.

Кросворд « Піраміда»

Слова по горизонталі: (Увага: в клітинці з цифрою букву не ставити) 1.Висота бічної грані правильної піраміди. 

2.Розділ математики, в якому вивчаються властивості геометричних фігур.

3. Відрізки, що з'єднують вершину піраміди з площиною основи.

4.Плоский многокутник, що не є бічною гранню піраміди.

5.Що знаходять за формулою:

6.Многогранник, але не піраміда.

7.Правильна трикутна піраміда. 8.Основа правильної чотирикутної піраміди. 

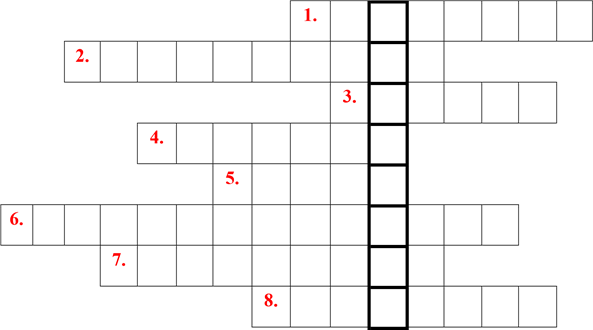
      Відповідь: