Розробка уроку "Розв'язування квадратних рівнянь", алгебра 8 клас
Конспект+презентація до уроку з алгебри "Розв'язування квадратних рівнянь", 8 клас. На уроці поєднана парна, колективна, самостійна робота та підготовка учнів до ЗНО.
Тема. Розв’язування квадратних рівнянь
Мета: повторити означення квадратного рівняння, повторити формули для визначення дискримінанта квадратного рівняння, формул для обчислення коренів квадратного рівняння, продовжити формувати вміння розв’язувати квадратні рівняння; перевірити вміння учнів застосовувати набуті знання на практиці; розвивати логічне та критичне мислення, пам’ять, увагу; розвивати знання учнів про рівняння; виховувати інтерес до математики, створювати умови для розвитку творчої особистості.
Тип уроку: застосування знань, навичок та вмінь
Форми проведення: робота в парах (розшифрування анаграми, вправа "Установіть відповідність"), колективна робота (розв’язування рівнянь), індивідуальна робота (тестова робота, розв’язування квадратних рівнянь), робота в групах (гра «Поле чудес»)
Методи проведення: словесні, інформаційні (історична довідка), пошукові (гра «Поле чудес», коментоване розв’язання рівнянь), елементи інтерактивних технологій (вправа «Асоціативний кущ»)
Обладнання: проектор, ПК, презентація вчителя, картки (картка № 1 «Тестова робота», картка № 2 «Установити відповідність», картка № 3 Матемаитична гра «Поле чудес»), бонусні жетони.
СТРУКТУРА УРОКУ
І. Організаційна частина (1 хв.)
ІІ. Перевірка домашнього завдання (1 хв.)
ІІІ. Формулювання теми, мети й завдань уроку (2 хв.)
Інтерактивна вправа «Анаграма»
Повідомлення теми, мети уроку
IV. Актуалізація опорних знань (11 хв.)
4.1 Теоретичний блок
Тестова робота (6 хв)
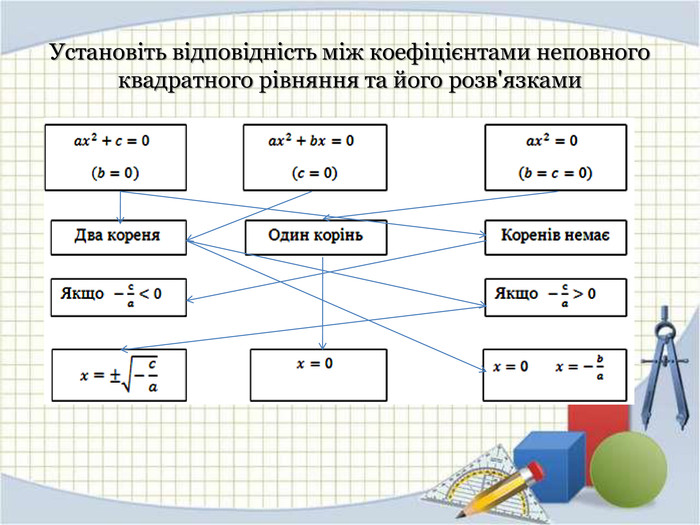
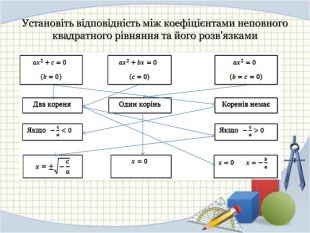
Установіть відповідність (2 хв.)
4.2. Практичний блок (розв'язування квадратних рівнянь) (3 хв.)
V. Застосування вмінь та навичок (25 хв.)
5.1. Математична гра "Поле чудес" (5 хв)
Фізкультхвилинка
5.2. Самостійна робота (10 хв.)
5.3. Коментоване розв'язання рівнянь (10 хв.)
VI. Підсумки уроку. Рефлексія (2 хв.)
VII. Домашнє завдання (1 хв.)
ХІД УРОКУ
І. Організаційна частина (слайд № 1)
Побажання вчителя: невідомо хто, коли але хтось сказав слова, які передаються нам і які ми передаємо нашим нащадкам: «Намагайтесь кожного дня для кожної справи знайти якийсь позитивний початок, оскільки від того настрою, з яким ви вступаєте в день, або в якусь справу, залежать ваші успіхи, а можливо і невдачі»
Я бажаю вам розпочати урок гарним настроєм і отримати від нього задоволення і гарні результати.
ІІ. Перевірка домашнього завдання (слайд № 2)

ІІІ. Формування теми, мети й завдань уроку. Мотивація навчальної діяльності
Анаграма (слайд № 3).
Виключіть зайве слово: таиімдкисрнн (дискримінант), рідізвок (відрізок), ірокнь (корінь), нівярянн (рівняння), фекоцінєті (коефіцієнт).
- Яка тема об’єднує решту слів? (Квадратні рівняння.)
Сьогодні ми будемо продовжувати працювати в рамках великої теми «Квадратні рівняння». Ця тема посідає почесне місце в математиці. Вона обов’язково має своє відображення під час складання ДПА та ЗНО (слайд № 4)
Отже, тема уроку «Розв’язування квадратних рівнянь».
- Запишіть, будь ласка число, число, класна робота та тему уроку до ваших зошитів.
- Якою на вашу думку буде мета сьогоднішнього уроку?
- Актуалізація опорних знань
І блок. теоретична частина
Прислів’я каже «Повторення – це мати навчання»
- Тестова робота (слайд № 5)
Кожна правильна відповідь – 0,25 б., максимальна оцінка – 3 бали
-
Рівняння, що зводяться до вигляду
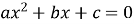 , де
, де 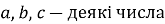 ,
, 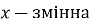 ,
, 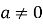 називається … рівняння
називається … рівняння
А. лінійним
Б. квадратним
В. дробово-раціональними
-
Квадратне рівняння, у якого коефіцієнт
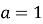 , називається …
, називається …
А. повним
Б. зведеним
В. неповним
Г. незведеним
-
Квадратне рівняння, у якого коефіцієнти
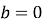 або
або 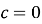 , називається …
, називається …
А. повним
Б. зведеним
В. неповним
Г. незведеним
- Формула дискримінанта…
А. ![]()
Б. ![]()
В. ![]()
Г. ![]()
- Формула коренів квадратного рівняння …
А. ![]() ,
, ![]()
Б. ![]() ,
, ![]()
В. ![]() ,
, ![]()
Г. ![]() ,
, ![]()
-
Якщо
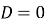 , то квадратне рівняння має …
, то квадратне рівняння має …
А. два корені
Б. один корінь
В. не має коренів
-
Якщо
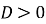 , то квадратне рівняння має …
, то квадратне рівняння має …
А. два корені
Б. один корінь
В. не має коренів
-
Якщо
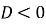 , то квадратне рівняння має …
, то квадратне рівняння має …
А. два корені
Б. один корінь
В. не має коренів
-
Старший коефіцієнт рівняння
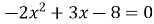
А. ![]()
Б.![]()
В. ![]()
Г. ![]()
-
Другий коефіцієнт рівняння
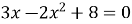
А. ![]()
Б.![]()
В. ![]()
Г. ![]()
-
Вільний член рівняння
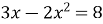
А. ![]()
Б. 8
В. ![]()
Г. ![]()
-
Рівняння виду
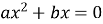 має …
має …
А. два корені
Б. немає коренів
В. один корінь
Самоперевірка тестової роботи (слайд № 5)
- Робота в парах (слайд № 6)
За допомогою стрілок покажіть зв'язок між коефіцієнтами неповного квадратного рівняння (2 бала)
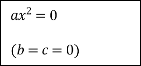
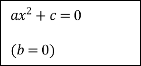
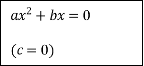
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
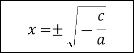
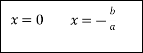

ІІ блок. Практична частина:
Розв’язати квадратні рівняння (3 учні працюють біля дошки)
а) ![]()
б) ![]()
в) ![]()
- Застосування вмінь та навичок
- Робота в групі
Історична довідка. (слайд № 7,8)
Чи знаєте ви, що квадратні рівняння вміли розв’язувати ще у Вавилоні за 2000-1700 років до нашої ери. Займалися розв’язуванням рівнянь багато вчених-математиків. Ім’я одного з них дізнаємося, коли пограємо у гру математичне «Поле чудес».
А ![]()
Д ![]()
І ![]()
Н ![]()
О ![]()
Т ![]()
Ф ![]()
Е ![]()
1. Яке рівняння можна розв’язати добуванням коренів квадратних? (Д)
2. Яке рівняння можна розв’язати способом винесення спільного множника за дужки? (І)
3. Яке рівняння можна розв’язати, представивши його ліву частину у вигляді квадрата двочлена? (О)
4. В якому рівнянні треба застосувати загальну формулу коренів квадратного рівняння? (Ф)
5. Яке з рівнянь не має розв’язків? (А)
6. Вкажіть рівняння, що має один розв’язок, який дорівнює нулю. (Н)
7. Яке рівняння можна розв’язати, застосувавши формулу різниці квадратів? (Т)
В результаті отримали ім’я ДІОФАНТ (слайд № 10).
Ну що ж, ім’я вченого розгадали, а от рівняння залишились нерозв’язаними.
- Самостійна робота (слайд №11 )
Ця частина уроку проходить під девізом: «Математику не можна вивчити, спостерігаючи, як це робить сусід» (А. Нівен – американський математик)
- Завдання. Розв’язати рівняння:
1) ![]() (0, 5 б.)
(0, 5 б.)
2) ![]() (0,5 б.)
(0,5 б.)
3) ![]() (0,5 б.)
(0,5 б.)
4) ![]() (0,5 б.)
(0,5 б.)
5) ![]() (0,5 б.)
(0,5 б.)
6) ![]() (0,5 б.)
(0,5 б.)
7) ![]() (1 б.)
(1 б.)
- Самоперевірка (слайд № 11)
- Коментоване розв’язання рівнянь (слайд № 12, 13)
Готуємося до ЗНО та ДПА
(2007 рік) Розв’яжіть рівняння ![]() . У відповідь запишіть суму коренів
. У відповідь запишіть суму коренів
Розв’яжіть рівняння ![]()
Додатково: Розв'яжіть рівняння ![]() . Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток
. Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток
- Підсумки уроку. Оцінювання (слайд № 14)
А зараз я хочу, аби ви оцінили результативність своєї роботи на уроці, використовуючи 12-бальну шкалу, зображену на слайді:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
- Домашнє завдання (слайд № 15)
- Випереджуюче домашнє завдання
Не можна не згадати ім’я французького математика Вієта, якого називають «батьком алгебри». Він першим почав позначати буквами не лише змінні, а й коефіцієнти. Це дало можливість узагальнити способи розв’язування рівнянь. Але це буде темою нашого наступного уроку. Тому самим допитливим учням ми дамо завдання: підготувати повідомлення про Франсуа Вієта та його відому теорему щодо коренів квадратного рівняння.
- Повторити § 3 п. 18-19
Розв’язати № 637 (2), № 639 (1), № 642
Картка № 3 Математична гра «Поле чудес»
А ![]()
Д ![]()
І ![]()
Н ![]()
О ![]()
Т ![]()
Ф ![]()
Е ![]()
1. Яке рівняння можна розв’язати добуванням коренів квадратних? (Д)
2. Яке рівняння можна розв’язати способом винесення спільного множника за дужки? (І)
3. Яке рівняння можна розв’язати, представивши його ліву частину у вигляді квадрата двочлена? (О)
4. В якому рівнянні треба застосувати загальну формулу коренів квадратного рівняння? (Ф)
5. Яке з рівнянь не має розв’язків? (А)
6. Вкажіть рівняння, що має один розв’язок, який дорівнює нулю. (Н)
7. Яке рівняння можна розв’язати, застосувавши формулу різниці квадратів? (Т)
Картка № 3 Математична гра «Поле чудес»
А ![]()
Д ![]()
І ![]()
Н ![]()
О ![]()
Т ![]()
Ф ![]()
Е ![]()
1. Яке рівняння можна розв’язати добуванням коренів квадратних? (Д)
2. Яке рівняння можна розв’язати способом винесення спільного множника за дужки? (І)
3. Яке рівняння можна розв’язати, представивши його ліву частину у вигляді квадрата двочлена? (О)
4. В якому рівнянні треба застосувати загальну формулу коренів квадратного рівняння? (Ф)
5. Яке з рівнянь не має розв’язків? (А)
6. Вкажіть рівняння, що має один розв’язок, який дорівнює нулю. (Н)
7. Яке рівняння можна розв’язати, застосувавши формулу різниці квадратів? (Т)
Картка № 2 Установіть відповідність
За допомогою стрілок покажіть зв'язок між коефіцієнтами неповного квадратного рівняння та його розв'язками
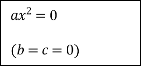
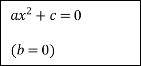
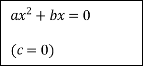
![]()
![]()
![]()
![]()
![]()
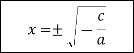

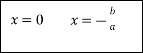
Картка № 2 Установіть відповідність
За допомогою стрілок покажіть зв'язок між коефіцієнтами неповного квадратного рівняння та його розв'язками
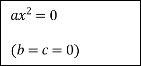
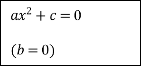
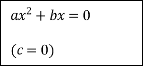
![]()
![]()
![]()
![]()
![]()
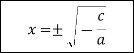

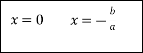
Картка № 1 Тестова робота
Кожна правильна відповідь – 0,25 б., максимальна оцінка – 3 бали
1. Рівняння, що зводяться до вигляду ![]() , де
, де ![]() ,
, ![]() ,
, ![]() називається … рівнянням
називається … рівнянням
А. лінійним
Б. квадратним
В. дробово-раціональними
2. Квадратне рівняння, у якого коефіцієнт ![]() , називається …
, називається …
А. повним
Б. зведеним
В. неповним
Г. незведеним
3. Квадратне рівняння, у якого коефіцієнти ![]() або
або ![]() , називається …
, називається …
А. повним
Б. зведеним
В. неповним
Г. незведеним
4. Формула дискримінанта…
А. ![]()
Б. ![]()
В. ![]()
Г. ![]()
5. Формула коренів квадратного рівняння …
А. ![]() ,
, ![]()
Б. ![]() ,
, ![]()
В. ![]() ,
, ![]()
Г. ![]() ,
, ![]()
6. Якщо ![]() , то квадратне рівняння має …
, то квадратне рівняння має …
А. два корені
Б. один корінь
В. не має коренів
7. Якщо ![]() , то квадратне рівняння має …
, то квадратне рівняння має …
А. два корені
Б. один корінь
В. не має коренів
8. Якщо ![]() , то квадратне рівняння …
, то квадратне рівняння …
А. два корені
Б. один корінь
В. не має коренів
9. Старший коефіцієнт рівняння ![]()
А. ![]()
Б.![]()
В. ![]()
Г. ![]()
10. Другий коефіцієнт рівняння ![]()
А. ![]()
Б.![]()
В. ![]()
Г. ![]()
11. Вільний член рівняння ![]()
А. ![]()
Б. 8
В. ![]()
Г. ![]()
12. Рівняння виду ![]() має …
має …
А. два корені
Б. немає коренів
В. один корінь
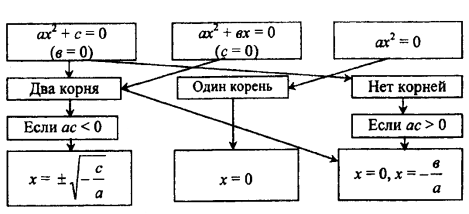
Схема розв’язання квадратних рівнянь
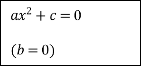
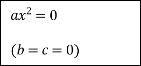
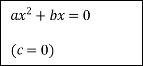
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
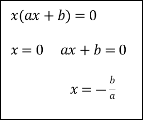
![]()
![]()
![]()
![]()
![]()
![]()
![]()
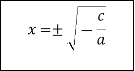
Схема розв’язання квадратних рівнянь
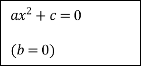
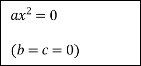
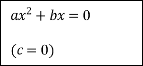
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
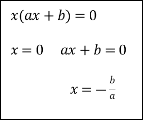
![]()
![]()
![]()
![]()
![]()
![]()
![]()
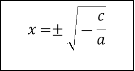

Ответы учащиеся проверяют с помощью взаимопроверки.
Готуємося до ЗНО та ДПА
-
(2007 рік) Розв’яжіть рівняння
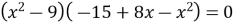 . У відповідь запишіть суму коренів
. У відповідь запишіть суму коренів
-
Розв’яжіть рівняння
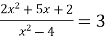
Додатково: Розв'яжіть рівняння ![]() . Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток
. Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток
Готуємося до ЗНО та ДПА
-
(2007 рік) Розв’яжіть рівняння
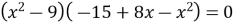 . У відповідь запишіть суму коренів
. У відповідь запишіть суму коренів
-
Розв’яжіть рівняння
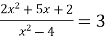
Додатково: Розв'яжіть рівняння ![]() . Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток
. Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток
Готуємося до ЗНО та ДПА
-
(2007 рік) Розв’яжіть рівняння
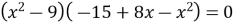 . У відповідь запишіть суму коренів
. У відповідь запишіть суму коренів
-
Розв’яжіть рівняння
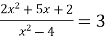
Додатково: Розв'яжіть рівняння ![]() . Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток
. Якщо рівняння має кілька коренів, то у відповідь запишіть їх добуток


про публікацію авторської розробки
Додати розробку