Сценарій  телепередачі «Неймовірна математика»

Слайд1

Ведучий 1.

 Доброго дня, дорогі друзі, любі телеглядачі ! Ми раді вітати вас на нашому новому каналі «Ця неймовірна математика»

Слайд 2

Ведучий 2

На нашому каналі ви зможете дізнатися безліч цікавих новин про таємниці всесвіту, про нерозв’язні математичні задачі,  зумієте ознайомитися з математичними парадоксами і софізмами, побачити різноманітні математичні ілюзії,  почуєте корисні поради, як стати мільйонером, як з мухи зробити слона та багато іншого

Слайд 3

Ведучий 1.

 Залишайтесь з нами і ви потрапите в світ нового, не завжди зрозумілого, але такого цікавого

Ведучий 2.

Ще давньогрецькі вчені натрапили на нерозв'язні задачі  в математиці. Вони докладали багато зусиль, щоб виявити механізми утворення таких загадок.

Слайд 4

Ведучий 1.

 Вчені боляче переживали такі невдачі. Давньогрецький фі­лософ Діодор Кронос (пом. бл. 307 р. до н. е.), не розв'язавши однієї з найдавніших логічних загадок – парадоксу Евбуліда, помер від розпачу, а другий філософ Філет Косський, зазнавши такої самої невдачі, покінчив життя самогубством.

Слайд5

Ведучий 2

Нерозв'язність задач, з якими зустрілися Діодор Кронос та Філет Колосський, пояснюється, як правило, порушенням законів логіки.

Слайд 6

Ведучий 1

Людині властиво помилятися. Тому дуже важливо, щоб вона вміла виявляти свої та чужі помилки, вчилась уникати їх, саме для цього і створено нашу телепередачу

Слайд7

Ведучий 2.

А з нами  на зв’язку наш кореспондент. Давайте в нього дізнаємося про новини  у фінансовій сфері та бізнесі.

Слайд 8

 Кореспондент 1.

цікаво вам, як швидко стати мільйонером????

Поспілкувавшись з вченими-софістами я дізнався про  спосіб швидкого збільшення свого капіталу.

  У вас є 2 грн. = 200 коп. Піднесемо ліву та праву частину рівності до квадрату:

 ( 2 грн .)² = ( 200 коп.)². Отримаємо 4 грн = 40000 коп. =400грн.

Наступний слайд 9

Ведучий 1.

 Дуже дякуємо за інформацію Як бачимо, стати мільйонером досить просто, але як зробити з мухи слона? На зв’язку наш кореспондент із Греції.

слайд 10

Кореспондент 2 (презентація)

Доброго дня, шановні телеглядачі, отож послухайте новини. Софістами древньої Греції доведено, що маса слона рівна масі мухи. Припускали, що а (г) – маса мухи, b (г) – маса слона. Позначили середнє арифметичне їх мас v: . Перемножимо почленно дві останні рівності і отримали:

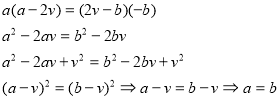
Спробуйте знайти помилку у міркуваннях!

Слайд 11

Реклама

Лунає мелодія пісні “Дважды два – четыре”. (діти під лану мелодію танцюють».

Ведучий2

Зараз наш кореспондент знаходиться в одній математичній лабораторії де відбуваються надзвичайно дивовижні відкриття. Виявляться що 2 помножити на два це не 4, як співалось в пісні, а 5 .Давайте з вами переглянемо це. Вашій увазі пряме включення.

Слайд12

Учень 1. (презентація)   

     Я стверджую, що 2^. 2 = 5  і можу це довести.

 Дійсно, розглянемо правильну числову рівність 4 : 4 = 5 : 5.

 Винесемо у кожній частині спільний множник  4( 1 :1) = 5 ( 1 : 1).

 Числа у дужках рівні,  тому 4= 5, тобто 2 ^. 2 = 5.

Слайд13

Учень 2.(презентація)

 І я також переконаний , що "4 = 5". Спробую довести вам своїм способом
  Нехай а=в+с. Помножимо обидві частини на 5: 5а=5в+5с. Додавши почленно цю рівність до рівності 4в+4с=4а і віднявши від обох частин утвореної рівності по 9а, матимемо:
   4в+4с-4а=5в+5с-5а, або
   4(в+с-а)=5(в+с-а).
   Звідси 4=5.
Ведучий 1.

Цикл наших передач продовжує фільм Степана Олійника “Синок – математик”( сценка)

Слайд 14

Автор .До батьків, до Яблунова,

             В рідну хату і садок

              З політехніки зі Львова

              Гостювать прибув синок.

              На обід прибув, до речі,

              (Стіл накрили в акурат!)

              Мати вийняла із печі

               Двоє смажених курчат.

               Син підняв до стелі руку:

Син       Ось курчата ці: фактично

              Двійко тут, як не бери.

              А візьми математично,

              Помудруй – і вийде три!

Батько Не мели дурницю синку!..-

Автор (І, як видно, розізлив).

            Той схопивсь:

Син     Одну хвилинку!-

 Автор  Щось помножив, поділив...

  Син       Ось вам рівно троє.

              Доказ точний і ясний! –

Автор. І промовив до старої

           Сивий батько мовчазний:

Батько  Якщо так виходить в Петі,

              Будуть двоє ці для нас,

              Він хай їсть оте вже, третє!

              Всім по одному якраз!

Слайд 15

Ведучий 2.

А ми знову з вами.  Я сподіваюсь, що Петя надалі запам’ятає свої математичні міркування. А от перед вами нова нерозгадана таємниця математики. Куди зникла тридцята гривня? Давайте послухаємо цю історію у телерепортажі із магазина ( софізм «Хитрий менеджер")

Кореспондент 3

 Доброго дня шановні телеглядачі. Я веду свій репортаж із книжкового магазину. Тут я почув ось таку історію. «Три дівчинки назбирали трохи грошей і вирішили придбати на трьох одну книжку, яка коштує 30 грн. Дівчатка скинулися по 10 грн і купили товар. Трохи згодом менеджер магазина довідався, що книжка коштує 25 грн і забрав із каси 5 грн. Менеджер мав віддати гроші дівчаткам, але як поділити 5 грн на трьох? Менеджер вирішив не ламати довго голову і віддав кожній дівчинці по 1 грн (отже, усього 3 грн), а 2 грн взяв собі. Отже, кожна дівчинка одержала назад по 1 грн, тобто замість 10 витратила 9 грн. 

    Нескладно порахувати, у скільки обійшлася дівчаткам книжка,  у 9*3=27 грн. Якщо до цих грошей додати ще 2 грн, які менеджер поклав собі у кишеню, отримаємо 29 грн. Куди зникла тридцята гривня?»

Ведучий 2.

О, я мабуть розгадав, цю таємницю. Важаю, що ви  неправильно рахуєте, скільки грошей було витрачено. Логічно буде сказати, що менеджер забрав у дівчат 2 грн. Оскільки 9*3=27, а книжка коштує 25 грн, не вистачає 2 грн. Тому додавати до 27 грн 2 грн просто некорректно, потрібно від 27грн відняти 2 грн.

Слайд 16

Ведучий 1.

Так, шановні глядачі, як бачимо, що помилившись в логічних міркуваннях ми отримуємо хибні висновки. А зараз вашій увазі знову пряме включення із математичної лабораторії. Тут відбуваються неймовірні нові відкриття.

Кореспондент.

Я знаходжуся в математичній лабораторії. Професоре, яке відкриття щойно тут відбулося?

Професор 6 (презентація)

Виявляється, що сума двох однакових чисел дорівнює нулю і хочу вам це я зараз довести. Доведу, що а+а=0. Нехай а=х. Помноживши обидві частини на -4а, дістанемо -4ах=-4а², або -4ах+4а²=0. Додамо до обох частин рівності х², тоді х²-4ах+4а²=х², або (х-2а)²=х², звідки х-2а=х. Але оскільки х=а, то а-2а=а, тобто -а=а. Остаточно: а+а=0.

Кореспондент.

Отож,  я вам дав 6 цукерок і мій колега теж. Ну і як смачно????

Професор.

 Але ж ви мені нічого не дали.

Кореспондент.

 Чому ж не дали. Адже по Ваших міркуваннях 6+6=0.Отож, ми Вам дали цукерки.

Слайд 17

Ведучий 2 .

Ви прослухали репортаж, який взяли у вченого-софіста. Сподіваюсь ви переконалися,  що цей софізм , як і будь-який інший, — це інтелектуальне шахрайство!
          Слайд 18

Ведучий 1.
Софізми зазвичай трактуються побіжно і з очевидним засудженням. І справді, чи задумувавались ви над таким  міркуваннями: «Той, що сидить встав; хто встав, той стоїть; отже, той, що сидить стоїть»
      Слайд 19

  Ведучий 2

Я знайомий із софізмом  «Рогатий» , який став знаменитим ще в Стародавній Греції. І зараз він кочує з енциклопедії в енциклопедію в якості «зразкового». З його допомогою можна запевнити кожного, що він рогатий: «Що ти не втрачав, то маєш; роги ти не втрачав; значить, у тебе роги». Втім, роги - це дрібниця порівняно з тим, що взагалі може бути доведено за допомогою цього і подібних йому міркувань.
        Слайд 20

Ведучий 1

Так це правда. А ось чи чули ви, шановні глядачі,  таке доведення: «Для того, щоб бачити, необов'язково мати очі, оскільки без правого ока ми бачимо, без лівого теж бачимо; окрім правого і лівого, інших очей у нас немає, тому ясно, що очі не є необхідними для зору»! ?

Слайд 21

Ведучий 2.

Так, це цікаво. А до вашої уваги на нашому телеканалі  історія двох софістів і простодушної людину на ім'я Ктесіпп, яку описав Платон.

Софіст 1.Скажи-ка, чи є у тебе собака?

Ктесіпп. Є. І дуже зла,

Софіст 2. А чи є у неї щенята?

Ктесіпп. Так, теж злі.

Софіст 1. А їх батько, звичайно, собака ж?

Ктесіпп. Так.

Софіст 2. І цей батько теж твій?

Ктесіпп . Звичайно.

Софіст 1.Значить, ти стверджуєш, що твій батько - собака і ти брат щенят!

 Слайд 22

Ведучий 1

Як бачимо, що переконати людину в тому, що у неї є роги, копита і хвіст, або що будь-який, довільно взятий батько, в тому числі і не є взагалі людиною, - це якраз її батько і т.д., можна тільки за допомогою обману або зловживання довірою. А це і є, як каже кримінальний кодекс, шахрайство.

Ведучий 2

Не випадково вчитель імператора Нерона давньоримський філософ... Сенека у своїх «Листах» кажучи про уявну переконливість софізмів порівнював їх з мистецтвом фокусників: ми не можемо сказати, як відбуваються їх маніпуляції, хоча твердо знаємо, що все робиться зовсім не так, як нам здається.

Ведучий 1.

Софізм є особливим прийомом інтелектуального шахрайства, спробою видати неправду за істину і тим самим ввести в оману.

Ведучий 2

Софізми відомі ще з античності, тоді вони використовувалися для обгрунтування явних безглуздостей, абсурду або парадоксальних положень, що суперечать загальноприйнятим уявленням. У Древній Греції софістика вважалася мистецтвом. Вірніше, не сама софістика, вміння перемагати в суперечках, природно використовуючи софістику. Цьому «мистецтву» навіть навчали в спеціальних школах

Ведучий 1.

А наш телеканал продовжує показ передач. Вашій увазі рубрика «Знаєш чи не знаєш?»

Слайд 23

Учень1. Чи знаєш ти те, про що я хочу тебе запитати?

Учень 2. Ні

Учень 1. Знаєш ти, що доброчесність є добро?

Учень 2.  Знаю.

Учень1. Про це я хотів запитати тебе. А ти, виходить, не знаєш те, що знаєш.   Учень2. Чи знаєш ти, про що я зараз хочу тебе запитати?
Учень1. Незнаю.
Учень2.  Невже ти незнаєш, що брехати — недобре?
Учень1 Звичайно, знаю.
Учень2. Але саме про це я і збирався тебе запитати, а ти відповів, що не знаєш.

Учень 1. А чи знаєш ти Миколу Шпарика із 11 класу?

Учень2. Так.

Учень1. А хто стоїть поряд з тобою?

Учень2. Не знаю.

Учень 1. Але це стоїть Микола Шпарик, а ти кажеш що його не знаєш

Ведучий 1 .

А я знаю, що тільки що ми переглянули не лише рубрику. «Знаєш чи не знаєш?», а й переглянули софізм «Покритий». Я знаю, скажімо, певну людину, але не знаю, що поряд зі мною, чимось накрившись, стоїть саме вона. Моя ствердна відповідь буде і вірною і невірною, оскільки я не знаю, що за чоловік поряд зі мною.

Ведучий 2.

А чи знаєте ви, шановні телеглядачі,  що М. І. Кондаков пояснює,  коли роз­глядати цей парадокс з погляду традиційної логіки, то він являє собою софізм, в якому є ніби двозначність дієслова «знати». Про вкриту людину не можна сказати, знаємо ми її чи не знаємо. Тому на питання потрібно відповідати так: «Оскільки ця людина вкрита, то мені невідомо, знаю я її чи не знаю». При такому підході софізм розв'язується легко.

Ведучий 1.

Я чув ще й таке, що той хто каже: «Я нічого не знаю», висловлює начебто парадоксальне, внутрішньо суперечливе твердження. Він заявляє, в сутності: «Я знаю, що я нічого не знаю». Але знання того, що ніякого знання немає, є все-таки знання. Значить, співрзмовник, з одного боку, запевняє, що ніякого знання у нього немає, а з іншого - самим затвердженням цього повідомляє, що деяке знання у нього все-таки є.

Ведучий 2.  

У чому тут справа? Розмірковуючи над цим,  можна згадати, що Сократ висловлював подібну думку більш обережно. Він говорив: «Я знаю тільки те, що нічого не знаю».

 Ведучий 1

Зате інший древній грек, Метродор, з повною переконаністю стверджував: «Нічого не знаю і не знаю навіть того, що я нічого не знаю». Чи немає в цьому твердженні парадоксу? Тож давайте послухаємо з вами інші відомі парадокси. Вашій увазі програма «Такий парадоксальний світ»

Слайд 24-25

Учень 1.

Парадокс «Брехун»

Крітянин Епіменід сказав: «Усі крітяни – брехуни». Епіменід – сам крітянин. Отже, він брехун. Але якщо Епіменід – брехун, тоді його висловлення «Всі крітяни – брехуни» хибне. Звідси випливає, що крітяни не брехуни, отже, й Епіменід не брехун, і тому його ви­словлення «Всі крітяни — брехуни» істинне.

Яке ж насправді висловлення Епіменіда: істинне чи хибне?

Слайд 26

Учень 2. (презентація)

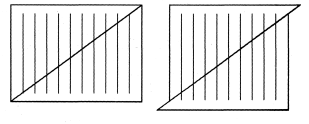
Накреслимо на прямокутному аркуші 10 вертикальних ліній однакової довжини. Проведемо діагональ. Розріжемо прямокутник по діагоналі і зсунемо нижню частину вниз, як показано на малюнку. Порахуємо кількість вертикальних ліній.

Їх стало 9! Де зникла ще одна лінія???

Слайд 27

Учень4.

Ліки

Ліки, прийняті хворим, є добро. Чим більше добра, тим краще. Значить, ліків потрібно приймати якомога більше.

Слайд 28

Учень 5

  Злодій

Злодій не бажає отримати нічого поганого. Придбання хорошого є гарна справа. Отже, злодій бажає гарного.

Слайд 29

Учень6

 Софізм «Купа»:

Різниця між купою і не - купою не в 1-ій піщинці.

Нехай у нас є купа піску. Починаємо з неї брати щоразу по одній піщинці. Продовжуємо цей процес. Якщо 100 піщинок - купа, то 99 - теж купа і т.д. .... 10 - купа, 9 - купа ... 3 - купа, 2 - купа, 1 - купа. Отже: суть софізму в тому, що кількісні зміни не призводять до якісних змін.

Слайд 30

Учень 7

Парадокс «Мер міста» полягає в наступному: кожен мер міста живе або в своєму місті, або поза ним. Був виданий наказ про виділення одного спеціального міста, де б жили тільки ті мери, які не живуть у своєму місті. Де має жити мер цього спеціального міста? Якщо він хоче жити у своєму місті, то він не може цього зробити, оскільки там можуть жити тільки мери, які не живуть у своєму місті, а якщо він не хоче жити у своєму місті, то, як і всі мери, які не живуть у своїх містах, він повинен жити у відведеному місті, тобто в своєму. Отже, він не може жити ні в своєму місті, ні поза ним.

Слайд 31

Учень 8

Парадокс «Генерал і цирульник» полягає в наступному: кожен солдат може сам себе голити або голитися в іншого солдата. Генерал видав наказ про виділення одного спеціального солдата-цирульника, у якого голилися б тільки ті солдати, які себе не голять. У кого повинен голитися цей спеціально виділений солдат-цирульник? Якщо він хоче сам себе голити, то він не може цього зробити, так як він може голити тільки тих солдат, які себе не голять, а якщо він не буде себе голити, то, як і всі солдати, які себе не голять, він повинен голитися тільки у одного спеціального солдата-цирульника, тобто у себе. Отже, він не може ні голити себе, ні не голити себе.

Слайд 32

Учень9.

 Зорові помилки та парадокси використав у своїх картинах відомий голландський художник Мауріц Корнеліус Ешер 1898-1972)

Слайд 33

Своїми малюнками він глузує з певних особливостей нашого сприймання тривимірного світу, створюючи насправді вражаючі, просто дивовижні ефекти.

Тож погляньмо, якими реалістичними є ці картини і спробуймо уявити, що нам потрібно  створити реальні об’єкти на основі них. Чи змогли б ви побудувати  такі конструкції з картону? Можливо хтось спробує?

Слайд 34

Неможливий водоспад

1961.Літографія. Конструкція складена з перекладин, які стоять одна на одній під прямим кутом. Слідкуючи за всіма елементами по черзі не помітно жодної невідповідності між ними. Але перед нами - абсолютно неможлива в цілому конструкція, оскільки в інтерпретації відстані між об'єктом і спостерігачем виникають дивні зміни.

Слайд 35

Літографія. 1960. Безмежні сходинки представляють головний мотив цієї картини. Прямокутник внутрішнього дворика замкнутий стінами будівлі, у якої замість даху - нескінченні сходинки.

Слайд 36-37

Учень 10.

Софізм Еватла

Еватл брав уроки софістики у давньогрецького софіста Протагора (бл. 481-411 до н.є.) з тією умовою, що гонорар він сплатить тільки в тому випадку, коли виграє свій перший судовий процес. Але після навчання Еватл не взявся вести жодного судового процесу і тому вважав, що може не платити гонорару Протагорові. Вчитель, погрожуючи подати на Еватла в суд, сказав:

– Незалежно від того, присудять судді платити мені гонорар чи не присудять, ти його обов'язково сплатиш. У першому випадку ти сплатиш за вироком суду, в другому – за нашою домовленістю.

На це Еватл, навчений Протагором мистецтву софістики, відповів:

– Ні в тому, ні в іншому випадку гонорару я не буду платити. Якщо мені присудять платити, то я не заплачу відповідно до нашої домовленості, бо програю свій перший судовий процес, у другому випадку я не платитиму відповідно до вироку суду.

Слайд 38

Учень 11

Але найзнаменитіший парадокс це, мабуть, парадокс Ахілла і Черепахи. Ахілл - герой і, як би ми зараз сказали, видатний спортсмен. Черепаха, як відомо, одне з найбільш повільних тварин. Тим не менш, Зенон стверджував, що Ахілл програє черепасі змагання в бігу. Приймемо наступні умови. Нехай Ахілла відокремлює від фінішу відстань С,  черепаху – Р. Рухатися Ахілл і черепаха починають одночасно. Нехай для визначеності Ахілл біжить в 2 рази швидше черепахи (тобто дуже повільно йде). Тоді, пробігши відстань Р , Ахілл виявить, що черепаха встигла за той же час подолати відрізок С і як і раніше знаходиться попереду героя. Далі картина повторюється: пробігши четверту частину шляху, Ахілл побачить черепаху на одній восьмій частині шляху попереду себе і т. д. Отже, щоразу, коли Ахілл долає відділяє його від черепахи відстань, остання встигає поповзти від нього і як і раніше залишається попереду. Таким чином, Ахілл ніколи не наздожене черепаху. Знаючі математичний аналіз зазвичай вказують, що ряд сходиться до 1. Тому, мовляв, Ахілл подолає весь шлях за кінцевий проміжок часу і, безумовно, обжене черепаху.

А на нашому телеканалі математичні частівки

Ми веселі дві подружки

Із баяном-братиком

Заспіваємо частівки

Вам про математику

Приспів: Та невже ми заспіваєм

                 Вам про математику

Розвязав Петрусь задачу,

Тільки мінус не побачив,

Ось і сталось, що лимон

Важить майже вісім тонн

Приспів:Та невже ото лимон

                Важить справді 8 тонн?

На контрольній ловив гав,

Одиницю упіймав,

Підглядав в усі книжки

Переплутав сторінки

Приспів: Та невже ото таки

                 Переплутав сторінки?

Біля дошки він стояв

І придумав чудо -

В теоремі прирівняв

До квадрата куба

Приспів: Та невже ото квадрата

                 Прирівняв до куба?

Хто задач не полюбляє,

Тим така і дяка -

Весь рік двійки заробляє

Вийде лобуряка

 Приспів: Та невже ото подяка –

                Двійки в лобуряки?

Слайд 39

Ведучий 2.

Отож, шановні телеглядачі ви переглянули телепередачу «Такий парадоксальний світ» та прослухали частівки. Описуючи життя Архімеда, римський історик Плутарх (50-125 pp.) стверджує, що великий математик вважав механізм важеля настільки досконалим, що сказав: «Дайте мені точку опори - і я зрушу Землю».

Ведучий 1.

А якщо й справді мати десь поза Землею точку опори, то якої довжини повинно бути одне плече важеля, щоб другим кінцем підняти Землю на 1 см.

Слайд 40

Ведучий 2.

Цю загадку всесвіту будуть розгадувати і далі нові й нові покоління людей. А вашій увазі фільм «Суперечка»

Софіст: Скажи, - може одна і та ж річ мати якусь властивість і не мати її?

Любитель суперечок: Очевидно, немає.

Софіст: Подивимося. Мед солодкий?

Любитель суперечок:  Так.

Софіст: І жовтий теж?

Любитель суперечок: Так, мед солодкий і жовтий. Але що з цього?

Софіст: Значить, мед солодкий і жовтий одночасно. Але жовтий - це солодкий чи ні?

Любитель суперечок: Звичайно, ні. Жовтий - це жовтий, а не солодкий.

Софіст:Значить, жовтий - це не солодкий?

Любитель суперечок: Звичайно.

Софіст:Про мед ти сказав, що він солодкий і жовтий, а потім погодився, що жовтий значить не солодкий, і тому як би сказав, що мед є солодким і не солодким одночасно. Адже спочатку ти твердо говорив, що жодна річ не може і володіти і не володіти якимось властивістю.

Слайд 41

Ведучий 2.

А ви шановні телеглядачі задумайтесь над останнім твердженням? Чи є тут помилка в міркуваннях?

Зараз вашій увазі телепередача «У світі математичної ілюзії»

Слайд 42

Ведучий 1.

Погляньте на решітку Герінга. На перетині всіх білих смуг, за виключенням того перетину, на якому ви фіксуєте погляд в даний момент, видно маленькі сірі п’ятна.

.

Слайд 43

Ведучий 2.

Погляньте на інший варіант решітки Герінга. На перетині чорних ліній можете помітити маленькі червоні цятки.

Слайд 44

Ведучий 1.

А це ілюзія  мигаючої решітки Білі кружечки здаються  мигаючими, так чи ні?

Слайд 45

Ведучий 2

Ахроматичний контраст. Круги мають один и той же відтінок сірого.

.

Ведучий 1.

В оточенні зеленого кольору сірий здається  бузково-ліловим, а в оточенні червоного - синьо-зеленим. Хроматичний контраст.

Слайд 46

Ведучий 2.

 Ілюзія Вертгеймера-Коффки Частина  кільця на білому фоні здається більш

темною при наявності олівця. Якщо ж його забрати, то ілюзія зникає.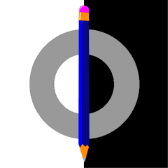


Слайд 47

Ведучий 1.

Не відриваючи погляду від центру круга, покрутіть головою.
Виникла ілюзія, що узор кругом кулі рухається. Здається, що чорні і білі полоски рухаються в різних напрямах?

 

Слайд 48

Ведучий 2.

 А це ілюзія  Брауна. Які круги рухаються швидше: великі чи малі? Насправді швидкість у них однакова.

Слайд 49

Ведучий 1.

Погляньте скільки кольорів на малюнку? Назвіть, які кольори є? Чи бачите голубі  чи зелені спіралі? А голубого тут нічого немає? Всі спіралі одного відтінку зеленого.

Слайд 50-51

Ведучий 2

 А ось  це фрактальна ілюзія. Чи не здається вам, що малюнок живий?

Слайд 52

Ведучий 1.

Фігури, які здаються спіралями, насправді є колами

Ведучий 2.

Ви переглянули телепередачу «У світі математичної ілюзії» . Сьогодні на нашому каналі ви ознайомилися  з відомими математичними софізмами і парадоксами, побачили неймовірні малюнки тривимірного простору і геометричних  ілюзій, попробували розв’язати задачі із явними логічними помилками.

Слайд 53

Ведучий 1.

Виявлення парадоксу змушує глибше проаналізувати нашу логічну інтуїцію і зайнятися систематичною переробкою основ науки логіки. Продовжуючи порівняння парадоксів з особливо виразними симптомами хвороби, можна сказати, що прагнення негайно виключити парадокси було б подібно бажанням зняти такі симптоми, особливо переймаючись про саму хворобу.

 Слайд 54

Ведучий 2.

Потрібно не просто знайти логічні помилки, необхідно їх пояснити, зміцнити і поглибити наші уявлення про логічні закономірності мислення. «Антиномии логіки, - пише фон Врігг, - спантеличили з моменту свого відкриття і, ймовірно, будуть спантеличувати нас завжди. Ми повинні, я думаю, розглядати їх не стільки як проблеми, що очікують рішення, скільки як невичерпно сирий матеріал для роздумів. Вони важливі, оскільки роздум про них зачіпає найбільш фундаментальні питання усієї логіки, а значить, і всього мислення 

Слайд 55

Ведучий 1.

 А Жан-Жак Руссо писав «Тисячі шляхів ведуть до помилки,

до істини – тільки один». Наш телеканал закінчує свою роботу і бажає всім телеглядачам знайти істину та  не допускати помилок у своєму житті.