Розробка уроку у 8 класі "Теорема Піфагора"

Про матеріал

В розробці пропонуються цікаві методи і прийоми на всіх етапах уроку.Зокрема дослідниций метод,частково-пошуковий,иипереджувальне навчання.ііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііііі

Перегляд файлу

Розробка уроку вчителя вищої категорії, вчителя-методиста Калинівської ЗОШ 1-3 ступенів №3, Вінницької обл. Галини Миколаївни Мороз

Тема уроку «Теорема Піфагора»

Тип уроку: урок засвоєння нових знань.

Мета уроку:

познайомити учнів з теоремою Піфагора, навчити доводити її та застосовувати до розв’язування задач;

- розвивати інтерес до вивчення математики;

- виховувати естетичні та художні смаки.

Обладнання: комп’ютер, мультимедійній проектор, інтерактивна дошка, презентація по темі, лінійки, транспортири, картки.

Хід уроку

На дошці епіграф:

Слайд 0

1. Організаційно- психологічний етап. Добрий день, друзі! Перед вами вислів одного з найвідоміших архітекторів 20 століття - француза -Ле Корбюзьє, який сказав: “Ніколи ще до нашого часу ми не жили в такий геометричний період… Навколишній світ – це світ геометрії. Чистий, істинний, бездоганний у наших очах. Усе навколо – ГЕОМЕТРІЯ” На слайді зображено портрет архітектора та будинок Центросоюзу (держкомстату) в Москві . На цьому гігантському «екрані» відображається картина московського неба, яка щохвилинно змінюється і рушить враження сухого геометризму, роблячи будівлю одним из самих поетичних творів функціональної арх.ітектури. Бо, справді, геометрія - це поетична наука, без якої не можна обійтись. здається, в самих банальних випадках. Ось послухайте.

До філософа одного

Завітав громадянин,

І стурбовано до нього:

«Хочу я поставить тин»

-В чому ж справа -

То й будуй!

Он і лози , он верба,

Є, що треба , де ж біда?

Справа, пане, тут у тім,
Що трикутний маю дім,
Щоб трикутна огорожа

Була гарна і пригожа!

Лиш трикутник не простий,

Прямокутний – не легкий!

Та на сторонах кута

Збудував я два крила,

А ось третю довжину,

Як дізнатись – не утну!

Мудрець лише посміхнувся

І до нього так звернувся:

Щоб робити щось руками,

Починать треба мізками!

І щоб тин добудувати

Про науку треба дбати,

Й теорему головну

Треба вивчить до ладу!

І тоді , лише, мій друже,

Ти знайдеш гіпотенузу!

Отже, ви зрозуміли, що без знань геометрії навіть тин збудувати не просто.

11.Мотивація навчання. Сьогодні на уроці ми вивчимо з вами найважливішу і найкрасивішу теорему геометрії , яка дасть нам можливість дуже легко і просто знаходити сторону прямокутного трикутника, якщо відомі дві інші його сторони, але для цього ми повинні повторити матеріал попередніх уроків.

111. Перевірка домашнього завдання.

(Учитель збирає зошити для перевірки)

1V.Актуалізація опорних знань

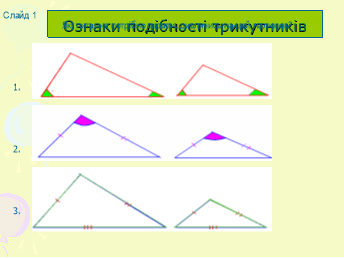
1.Які питання потрібно задати, дивлячись на цей малюнок?(ефекти анімації)

(учні самі задають запитання до кожного малюнка)(Слайд1)

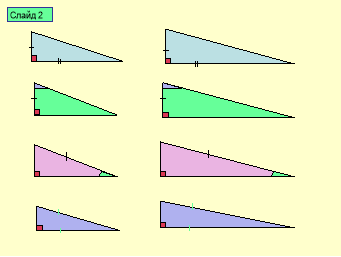
2. Які ознаки прямокутних трикутників ілюструють ці малюнки? Сформулюйте їх.(Слайд 2)

3.Продовж речення (ефект анімації)(Слайд 3)

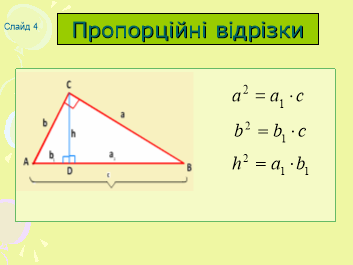
4.Вкажіть середні пропорційні відрізки( ефект анімації)(Слайд 4)

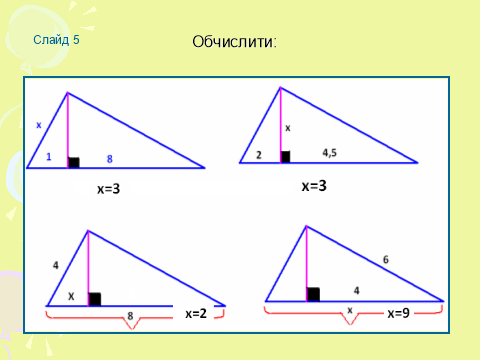
5.Обчислити невідомий відрізок ( ефект анімації)(Слайд 5)

Учитель дякує учнів за гарну працю.

1V. Оголошення теми уроку.(Звучить інструментальна музика. Учитель читає поетичні рядки) (демонструються слайди 6-12)

Отже , друзі, ви зрозуміли, що далі мова піде про найвизначнішу теорему геометрії - теорему, про яку академік Александров сказав(слайд 13)

Ця теорема народилася дві з половиною тисячі років тому і її батьком є відомий грецький математик і філософ – Піфагор. Із переказів та легенд, які до нас дійшли ми дізнаємось, що коли Піфагор довів свою теорему, він був настільки приголомшений, що звелів засмажити 100 волів та принести їх у жертву богам, але як це було насправді достеменно не відомо.

Отже, тема нашого уроку ?(учні)

V.Пояснення нового матеріалу

Метод навчання: дослідницький. (Учням роздані картки)

У чому ж суть цієї теореми? Для того щоб дати відповідь на це запитання проведемо дослідження.

І, я впевнена, що ви самі знайдете відповідь на це запитання. Отже перед вами лежать картки ,

на яких зображено три різних ,довільно вибраних, прямокутних трикутники. (слайд 14)

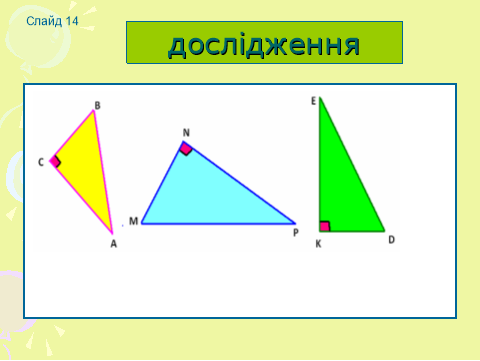
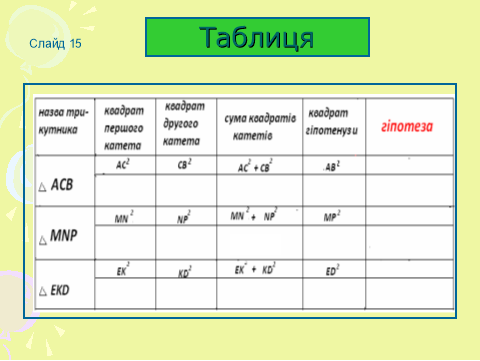
Ваше завдання виміряти катети кожного трикутника та їх гіпотенузу і записати їх квадрати у таблицю:

(слайд 15)

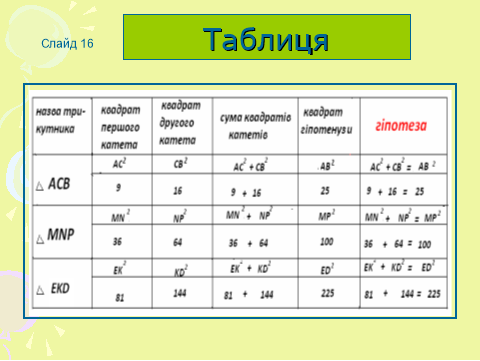
А тепер порівняйте результати : суму квадратів катетів і квадрат гіпотенузи?( Учні висловлюють гіпотезу)Отже , проаналізувавши наші вимірювання ми побачили, що?(Учні) - що квадрат гіпотенузи у всіх трьох трикутниках дорівнює сумі квадратів катетів. (слайд 16)

А чи справедливе це твердження для всіх на світі прямокутних трикутників? Це саме запитання задав собі і Піфагор і успішно на нього відповів, довівши його, але, на жаль, його доведення до нас не дійшло. Доведень цієї теореми на сьогоднішній день відомо більше 100, але ми зупинимось лише на одному. Отже, нам потрібно довести, що?(учні відповідають) (слайд 17)

Метод навчання: частково – пошуковий. (слайд 18)(ефект анімації)

- Що дано в теоремі?(Прямокутний трикутник)

- Що потрібно довести?( )

- Яку добудову потрібно зробити для доведення ?

- Як називається відрізок АН?НВ?

- Який зв’язок між катетами прямокутного трикутника АСВ ,їх проекціями на гіпотенузу і гіпотенузою?

Отже , яку теорему ми довели?( декілька учнів відповідають).

Запитання:

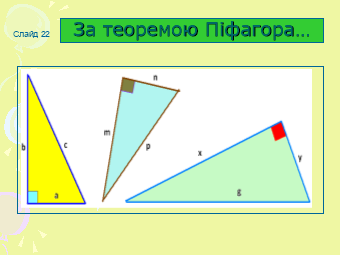
Як знайти гіпотенузу за відомими катетами? (слайд 19)

Як знайти невідомий катет , якщо відомо гіпотенузу і другий катет? (слайд 20)

Технологія випереджувального навчання: Крім доведення, яке ми привели, існують інші доведення теореми Піфагора.(Один з учнів може пояснити суть цього доведення, познайомившись з ним наперед, за дорученням учителя.)

V1. Закріплення вивченого.

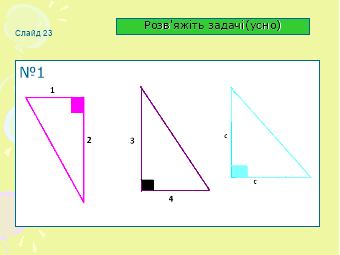
Задача №1.( Слайд 22)Користуючись теоремою

Піфагора, вказати які рівності відповідають кожному малюнку.

Розв’яжіть задачі(усно №1) ( слайд 23 )

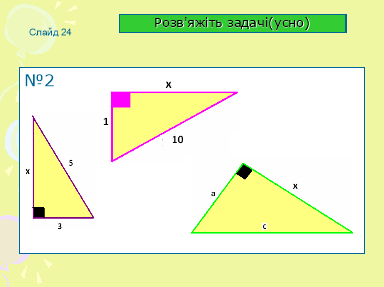
У цій задачі ми шукали гіпотенузу, коли відомі катети, а чи не можна знайти невідомий катет, якщо відомий другий катет і гіпотенуза?

Задача (усно №2) ( слайд 24 )

Заповніть таблицю( слайд 25, (26)

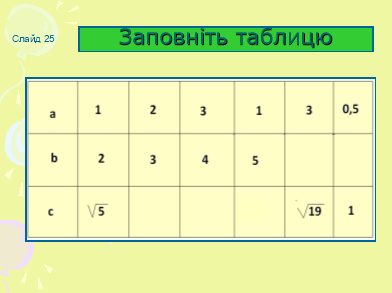
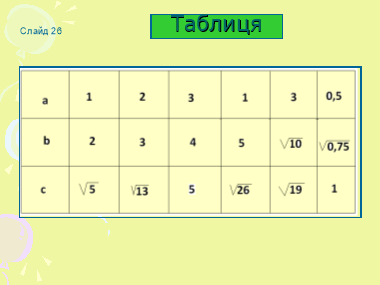
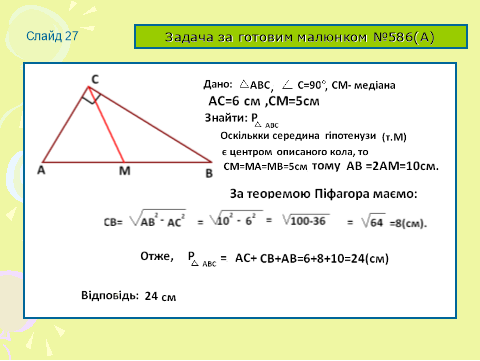
Колективне розв’язання №586(а)(слайд 27)Робота з картками.(учням роздані картки з готовими малюнками).Учень працює біля дошки. Паралельно перевірка розв’язання демонструється на мультимедійній дошці.

Робота в парах: .№596(а) (Учням роздані картки з пропущеними логічними кроками у розв’язанні задачі) Задача-підказка: Замінити знак « ?» відповідним кроком розв’язання)(слайд28)

Правильність заповнених прогалин перевіряється на слайді 28.