РОзробка уроку в 9 класі"Формула n-го члена арифметичної прогресії"

 

Розробка уроку вчителя вищої категорії, вчителя-методиста Калинівської ЗОШ 1-3 ступенів №3, Вінницької обл. Галини Миколаївни Мороз.       

Тема уроку «Арифметична прогресія. Формула  n-го члена  арифметичної прогресії»

Тип уроку: комбінований.

Форма уроку: урок-презентація.

 Обладнання: : комп’ютер, мультимедійній проектор, презентація по темі, картки.

Мета уроку : вдосконалити  знання учнів про зміст означення та властивостей арифметичної прогресії, вміння виділяти арифметичну прогресію серед інших числових послідовностей, знаходити різницю арифметичної прогресії та її перші члени, застосовувати  властивості арифметичної прогресії. Навчити доводити формулу  n- го члена арифметичної прогресії та використовувати її до розв’язування різних за з містом задач.

- розвивати логічне мислення, вміння аналізувати та синтезувати, інтерес до вивчення математики;

- виховувати культуру математичної мови, почуття взаємодопомоги та колективізму естетичні та художні смаки.

Хід уроку

 

На дошці епіграф:

 

1.Організаційно- психологічний етап.(1хв) Добрий день, друзі! Перед вами вислів  відомого англійського філософа, історика, політичного діяча Френсіса Бекона “У природі існує багато такого, що не може бути достатньо,  глибоко зрозуміло ні достатньо переконливо доведено,   ні досить уміло і надійно використано на практиці без допомоги втручання  математики ”(Слайд1)

(Далі звучить спокійна  прекрасна інструментальна мелодія, учитель читає поетичні рядки)(демонструється слайд 2, на якому  за допомогою ефекту анімації з'являються один за одним

 портрети М.В, Ломоносова. Г.Галілея, Л. да Вінчі і Ейнштейна.)

Природа, друзі, – це не витвір

Чиїхось марень і казок,

Це не бездумний образ -

Без суті, ролі і думок!

Природа – матінка говорить,

В природи,друзі, є душа,

І мова в неї є велична -

Красива , мудра і проста!

Математика – це написав Ломоносов,

Математика – це підтвердив Галілей,

Леонардо да Вінчі сказав своє слово,

А пізніше доповнив -

Дослідник великий  Ейнштейн!

 

 Отже,   прочитані поетичні рядки, ще раз  нагадали вам про те що  і числові послідовності -  це одна із  математичних моделей, яка  є вираженням результатів спостережень за реальними  фізичними, хімічними

 

 

 

 

 

процесами і природними явищами. І  сьогодні на уроці ми продовжимо вдосконалювати і розширювати свої знання  про одну із числових послідовностей , яка називається  арифметичною прогресією.

На парті в кожного учня  лежать картки  з таблицею – це «Накопичувальний кейс» . На протязі уроку учень має можливість сам собі ставити зароблені бали на кожному етапі уроку. В кінці уроку робиться підсумок знань і кожний може оцінити   свій  рівень.

 

Накопичувальний кейс
Прізвище
№п/п	Назва етапів уроку	Максимальна кількість балів	Отримана кількість балів	Шкала оцінювання	Оцінка
1	Робота в парах	4		40-47 балів	(12 балів)
2	Логічний ланцюжок	2		35-39 бали	(11 балів)
3	Магічний квадрат	1		30-34     бали	(10 балів)
4	Готуємось до ДПА	2		25-29   бали	(9 балів)
5	Робота в групах	3

11. Перевірка домашнього завдання.(4хв)

   Робота в парах.(Картка 1)(Результати виконання  перевіряються на слайді 3 і обговорюються)

 

1.(1 бал)Яка з наведених послідовностей  є арифметичною прогресією?

 

     а)1;5;8;12;          б)2;6;8;10;               в)7;10;12;15;                     г)-3;-1;1;4   ;

 

 

2. (1 бал)Перший член арифметичної прогресії дорівнює  - 6, а різниця 3.

.Чому дорівнює другий член цієї прогресії?

 

                      в)9;                     в)-3                        б) -9;                                 г)8;

 

3. (1 бал) Знайдіть різницю арифметичної прогресії (а), якщо а =5, а = -8.

 

                       а)3;                      б) -3;              в)13 ;                  г)-13;

4. (2 бали)Знайдіть різницю арифметичної прогресії (а), якщо а = 6, а = 24.

 

                    а)18;                    б) 9;                           в)30;                   г)-18;

 

ІІ1.Актуалізація опорних знань.(8 хв.)

 Прийом «Математичний волейбол».Клас  ділиться на дві команди. За  вказівкою вчителя  одна із команд робить перший « пас», тобто задає питання по темі, друга команда відповідає, якщо відповідь правильна ,  то   вже ця команда задає питання, інша відповідає і т . д. за кожне правильно задане питання, або правильну відповідь  учитель дарує учневі  1 бал.

Питання можуть бути такі:

  - що означає слово «прогресія»?

 - хто такий Леонардо Фібоначчі?

 - назвіть послідовність Фібоначчі;

 - що досить задати,щоб задати арифметичну прогресію?

 - що називається арифметичною прогресією?

 - що називається різницею арифметичної прогресії?

 - чому дорівнює сума членів арифметичної прогресії, рівновіддалених від її кінців?

 - задайте арифметичну прогресію  рекурентною формулою ;

 - чи є арифметична прогресія  функцією?

 - яку властивість має кожний член арифметичної прогресії, починаючи з другого?

 

 - назвіть область визначення  арифметичної прогресії;

- які є прогресії за кількістю членів?

-  чи може різниця арифметичної прогресії дорівнювати нулю?

-  чи є арифметичною прогресією  множина натуральних чисел7

-  чи може бути арифметична прогресія ні зростаючою, ні спадною?

-  різниця арифметичної прогресії дорівнює 2, чому дорівнює  ?

 

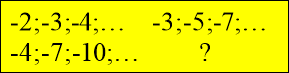
Прийом: «Логічний ланцюжок».(слайд 4) На кожному з  чотирьох завдань учні мають встановити логічний зв’язок між записами і знак запитання замінити наступним логічним кроком.

 

 

 

 

 

 

 

 

 

 

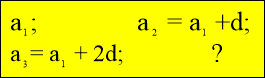
Це цікаво знати. Магічний квадрат. Яку особливість мають числа магічного (слайд 5)

квадрата?

11	21	7
9	13	17
19	5	15

 

                                               5;7;9;11;13;15;17;19;21;

 

Хто з великих художників епохи відродження зобразив магічний квадрат на своїй гравюрі?(після відповіді учнів на слайді з'являється  назва гравюри та ім'я художника)

 

 

 

На  слайдах 6 і 7  завдання на повторення « Готуємось до ДПА»

 

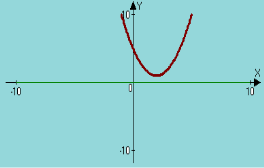
На рисунку зображено графік функції                                   

Назвіть множини розв'язків нерівностей:      

 

 

 

 

 

 

 

 

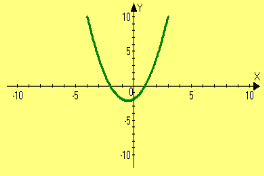Розв'яжіть нерівність:

 

 

 

 

 

 

 

 

 

1V.Мотивація навчальної діяльності.Оголошення мети і теми уроку.(1хв)

 

Задача. Знайти 150 член арифметичної прогресії():7;10;13;… .

     Запитання до учнів .Чи зручно  знаходити 150 член заданої прогресії за рекурентною формулою ?

  Чи не існує іншого шляху знаходження n-го  члена арифметичної прогресії?

 Отже, нашим завданням  сьогодні на уроці є відшукати цей шлях.

  Запишіть тему уроку «Формула  n-го члена арифметичної прогресії»

Технологія випереджувального навчання. Учитель дає завдання кільком учням самостійно підготувати виведення формули n-го члена арифметичної прогресії. Після того як учні опрацюють матеріал, учитель може  допомогти їм вибрати технологію подання нового матеріалу .Це може бути сократівський метод, коли шляхом навідних запитань учні самі відкривають істину.

V. Пояснення  нового матеріалу.(4 хв.) 

 Нехай дано арифметичну прогресію (): ,різниця якої дорівнює d.

Запитання до учнів:

• Чому дорівнює ()
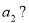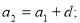• Чому  дорівнює ?(
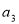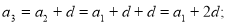
• Чому  дорівнює ?(
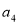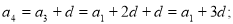
• Порівняйте  в отриманих формулах  порядковий  номер члена прогресії з коефіцієнтом біля d

     (Коефіцієнт при  d на 1 менший за порядковий номер члена прогресії)

• Чому дорівнює  ??(.
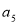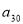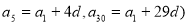• Отже,за цією логікою , чому дорівнює ?

 

 

 

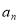• Назвіть що означає кожна буква отриманої  формули?

  Ця формула називається формулою n- го члена арифметичної прогресії.

• Що потрібно знати, .щоб  знайти будь-який член арифметичної прогресії?  

 

Робота  з підручником.(1хв.) Відкрийте підручник на ст.176  і прочитайте текст до слів  «Приклади розв’язання…»

V1. Первинне засвоєння знань.

Робота в різнорівневих  групах.(5хв.)(Учні об’єднуються за номерами 1,2,3,4)

Учні поділені на 4 різнорівневі  групи.(На розв’язання завдання кожній групі дається 1 хв.)

 Завдання для  групи 1.Знайти 11 член арифметичної прогресії():7;10;13;…

Завдання для  групи 2. Знайти  перший  член арифметичної прогресії(),

   у  якій d = -3,

Завдання для  групи 3.Чи є число   64 членом арифметичної прогресії, у якій 

Завдання для  групи 1V. Знайдіть порядковий номер члена   арифметичної прогресії, якщо

Після закінчення роботи лідер кожної групи робить необхідні пояснення біля дошки   , учні записують розв’язання в зошит.(Паралельно  розв’язання перевіряється  на слайдах 9-12)

Учні займають попередні місця.

Колективне розв’язання.№716.(4хв.)Біля дошки працює учень, кожний крок розв’язання  звіряється зі слайдом 9)

                                  Дано: ()арифметична прогресія.

 

                                  Знайти:      і 

                                               Розв'язання.

За формулою n- го члена  арифметичної  прогресії маємо:

 

 

 

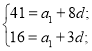
За умовою                             тому маємо систему:

 

 

Від першого рівняння віднімемо друге, отримаємо:

 

 

 

 

 

Відповідь:

Технологія  «Ажурна пилка».Робота в однорівневих групах (10хв.)(Учні об’єднуються за номерами  1;1;1;1,  2;2;2;2, 3;3;3;3. 4;4;4;4)

 

Завдання для  групи 1.(Об'єднання учнів з високим рівнем знань  )  №722.

Завдання для  групи 2.(Об'єднання учнів з достатнім  рівнем знань) №717.

Завдання для  групи 3.(Об'єднання учнів з середнім  рівнем знань)  №713

Завдання для  групи 4.(Об'єднання учнів з середнім  рівнем знань)  №706.

 

Після закінчення роботи  представник кожної групи озвучує результати розв’язання на клас біля дошки.

 

Результати  звіряються зі  слайдами

 

 

 

 

 

 

 

 

 

V11.Підсумок уроку. (1хв.))

 

Прийом   «Прогалини» .(Картка №2)

                    Заповніть прогалини таким чином, щоб рівність була правильною

 

                          1  варіант                                                                            11 варіант  

       1.                                                                                  1.

 

       2.                                                                                  2.  

 

       3.                                                                                 3.  

 

       4.                                                                              4.

 

       5.                                                                            5.         

 

 

V111. Контрольно -рефлексивной етап.  Учні підбивають підсумок  набраних балів в «Накопичувальному кейсі», оголошують  свої оцінки, учитель виставляє в журнал

Учитель пропонує прикріпити стікери з буквою «я» на плакаті, який  заготовлений наперед на закритій дошці «Піраміда успіху»

 

 

1X.Домашнє завдання:

 

Х. Закінчення уроку.