Розробка уроку з геометрії

Про матеріал

Розробка уроку з геометрії, з теми: «Площі поверхонь та об’єми геометричних тіл». ФОРМА ПРОВЕДЕННЯ: урок дослідження

Перегляд файлу

РОЗРОБКА УРОКУ

З ГЕОМЕТРІЇ

З ТЕМИ:

«Площі поверхонь та об’єми геометричних тіл».

Підготувала

викладачка: математики

Євгенія ЛЕБЕДЕВА

2023

МЕТА УРОКУ:

1. а) узагальнити і систематизувати знання учнів з теми: «Площі поверхонь та об`ємів геометричних» ;

б) закріпити навички розв’язування задач з даної теми;

в) показати практичне застосування вивченого матеріалу під час розв'язання задач;

2. Розвинути самостійність, почуття колективізму, уміння вислуховувати відповіді товаришів, розвинути інтерес до предмета;

3. Формувати і розвивати розумові операції (порівняння, узагальнення, систематизацію); розвивати творчі здібності, логічне мислення здобувачів освіти.

ФОРМУВАННЯ КОМПЕТЕНТНОСТЕЙ :

уміння вчитися впродовж життя — оцінювати результати своєї навчальної діяльності;

ініціативність і підприємливість — використовувати критерії раціональності, практичності, ефективності та точності з метою вибору найкращого рішення;

основні компетентності у природничих науках і технологіях — будувати та досліджувати математичні моделі процесів.

ТИП УРОКУ: вдосконалення вмінь і навичок при розв’язку задач

ОБЛАДНАННЯ: диференційовані картки-задачі, тестові завдання, макети фігур, проектор, мультимедійна дошка, ПК, зошит, підручник.

ФОРМА ПРОВЕДЕННЯ: урок дослідження

ПЛАН УРОКУ.

Організаційний момент (1 хв).
Актуалізація опорних знань учнів (10 хв).
Застосування знань і умінь при розв’язуванні задач , дослідницька інтерактивна гра (30 хв .).
Підсумок уроку (2 хв).
Домашнє завдання (2хв)

ХІД УРОКУ.

1.ОГОЛОШЕННЯ ТЕМИ ТА МЕТИ УРОКУ.

2.МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ ЗДОБУВАЧІВ ОСВІТИ

На мою думку, знання – це одна із сходинок до успіху в майбутньому. І сьогодні ми будемо плідно працювати, щоб досягнути мети. Отож метою нашого уроку є узагальнення та систематизація знань, умінь та навичок з теми «Площі поверхонь та об’єми геометричних тіл». Тому сьогодні на уроці ми будемо розв’язувати задачі з геометрії прикладного характеру, за допомогою яких розкриваються можливості реалізації зв’язку математичної та професійної підготовки здобувачів освіти.

Ви стоїте на порозі закінчення навчального закладу . Здавалось би, що після ліцею математика ніде не пригодиться. На жаль! Тут приходиться використовувати математику ще більше.

Практичні задачі геометричного змісту ─ найактуальніша тема для сьогоднішніх випускників. Ці завдання сприяють застосуванню отриманих знань в реальному житті.

Уміння вирішувати такі завдання допоможе адаптуватися в суспільстві.

АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ УЧНІВ

На платформі LearningApps.org здобувачі освіти виконують вправу за посиланням :

(https://learningapps.org/display?v=pkj7rpyuk22) або QR-Cod

(Один учень , біля мультимедійної дошки робить вправу )

Інтерактивна вправа «Мікрофон»

Дайте означення геометричного тіла
Дайте означення призми. Назвіть її елементи
Назвіть види призм
Дайте означення піраміди. Назвіть її елементи
Назвіть види пірамід
Дайте означення тіл обертання

4. УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ ПОНЯТЬ.

Сьогодні на уроці ми зі здобувачами освіти розглянемо принципи формування архітектури енергоефективних будинків (STEM – формат)

Розглянемо концепцію визначення раціональних пропорцій житлових будинків. Вона полягає в тому, що існує розроблений комплекс геометричних моделей, які дозволяють архітектору- проектувальникові в інтерактивному діалоговому режимі проектувальник-ЕОМ знаходити:

раціональні пропорції будинку;

оптимальні пропорції будинку ( тепловтрати на заданий рівень процентів перевищують раціональні);

визначити інтервал можливих пропорцій будинку тощо.

Унікальний економний будинок-купол, що був збудуваний українцем Валерієм Самойловим, зараз зайдемо за посиланням та переглянемо відео на YouTube

https://www.youtube.com/watch?v=Bi1H4YL9VbI ) за посиланням

або QR-Cod

Після перегляду відео, викладач з учнями починає Інтерактивну вправу під назвою «Дослідження»

Розв’язування задач в групах

Степаненко І. вважає, що необхідно робити форму будинку компактніше, з мінімальним відношенням площі зовнішніх огороджень до житлової площі будинку. Розглянувши такі види геометричних фігур, як: кулю, квадрат, витягнутий прямокутник, він зробив висновок, що ідеальною формою будинку буде куля, але оскільки їх не зручно будувати, тому оптимальною формою є квадрат. З точки зору зниження витрат на опалення будинку, найгіршою є будівля у вигляді високої вежі або витягнутої з порізаними фасадами. Ми розширимо перелік геометричних фігур, зробимо свої дослідження та одержимо результати, які проаналізуємо.

Розрахунки проведено для умовно взятої території забудови площею 200 м² ( 20 х 10 ) та висотою 10 м.

Учні поділяються на 5 груп, кожна з яких проведить розрахунки для геометричних тіл: паралелепіпеда, чотирикутної піраміди, циліндра, кулі, конуса.

1) Паралелепіпед.

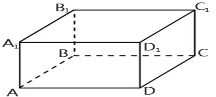Картинки по запросу рисунок паралелепіпеда Рис.1

Нехай ABCDA₁ B₁ C₁ D₁ – заданий паралелепіпед, в основі якого лежить прямокутник ABCD. Паралелепіпед має виміри a, b, с

( висота, довжина, ширина )

c = АВ = 10 м, b = AD = 20 м, a = АА₁ = 10 м.

V = abc,

V_парал. = 10·20·10 = 2000 ( м³).

S_{бічна пов.} = 2 (S₁+ S₂), S_{біч.пов}= 2 ( 20 ·10 + 10 · 10 ) = 600 ( м²).

S_основи = bc; S_основи = 20 · 10 = 200 ( м²).

S_{повна пов.} = S_{бічна пов.}+ 2 S_основи; S_{повна пов.} = 600 + 2· 200 = 1000 ( м²).

Обчислимо відношення

2) Чотирикутна піраміда.

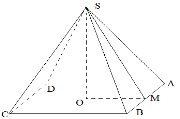Картинки по запросу рисунок чотирикутної піраміди Рис.2

Нехай SABCD – задана піраміда, в основі якої лежить прямокутник ABCD, AB = CD = 10 м, BC = AD = 20 м.

Бічні ребра піраміди SC = SA = SD = SB.

Висота SO (ABC ), OM AB, тоді за теоремою про три перпендикуляри SM AB, SO = 10 м.

S_основи ·H; S_основи= AB · BC: S_основи= 10 · 20 = 200 ( м²).

·200 · 10 = ( м³).

S_{бічна пов.} = 2 (S₁+ S₂), де S₁= , S₂= .

Оскільки AC, BD – діагоналі прямокутника, то за їх властивостями

AC BD = О, AО = CО = BО = DО = AC,

для знаходження AC розглянемо , у якого =90⁰,

AB = 10 м, BC = 20 м, тоді за теоремою Піфагора ,

(м), отже

AО = CО = BО = DО = · =(м).

Розглянемо , у якого =90⁰,

SO = 10 м, OB = м, тоді за теоремою Піфагора ,

(м), отже,

SC = SA = SD = SB = 15 м.

Розглянемо , у якого SC = SB = 15 м, SК СB, СВ = 20 м.

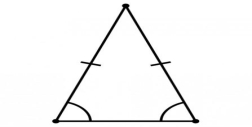Картинки по запросу площарівнобедреного трикутника Рис.3

C K B

Оскільки - рівнобедрений, то за йoго властивостями

СК = КВ = СВ, СК = КВ = ·20 = 10 ( м).

Розглянемо , у якого =90⁰,

SВ = 15 м, КB = 10 м, тоді за наслідком з теореми Піфагора ,

(м), отже, обчислимо

S₁= , , ( м²).

Розглянемо , у якого SA = SB = 15 м, SM AB, AВ = 10 м.

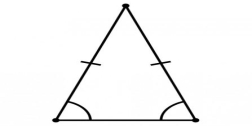Картинки по запросу площарівнобедреного трикутника Рис.4

B M A

Оскільки - рівнобедрений, то за йoго властивостями

BM = MA = AВ, BM = MA = ·10 = 5 ( м).

Розглянемо , у якого =90⁰,

SВ = 15 м, MB = 5 м, тоді за наслідком з теореми Піфагора ,

(м), отже обчислимо

S₂= . , ( м²).

Отже, обчислимо

S_{бічна пов.} = 2 ( 111,8034+ 70,7107) =2 ·182,5141 = 365,0282 ( м²).

S_{повна пов.} = S_{бічна пов.}+ S_основи;

S_{повна пов.} = 365,0282 + 200 = 565,0282( м²).

Обчислимо відношення

3) Циліндр.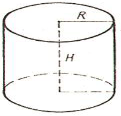 Картинки по запросу рисунок цилінлра

Рис.5

Нехай задано циліндр, у якого H = 10 м, R = 10 м.

; ( м³).

S_{бічна пов.} = ; S_{бічна пов.} = ( м²).

S_{повна пов.} = S_{бічна пов.}+ 2S_основи; S_основи= ; S_основи= ( м²).

S_{повна пов.} = 628 + 2·314 = 628 + 628 = 1256 ( м²).

Обчислимо відношення

4) Куля.

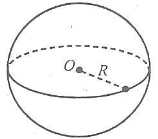Картинки по запросу кулі Рис.6

Нехай задано кулю, у якої R = 5 м.

; ( м³).

S_повна= S_сфери= ; S_повна= S_сфери= ( м²).

Обчислимо відношення

5) Конус.

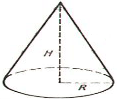Картинки по запросу рисунок конуса Рис.7

Нехай задано конус, у якого H = 10 м, R = 10 м.

; ( м³).

S_{бічна пов.} = ; де твірна.

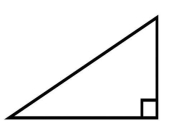
Для обчислення твірної розглянемо прямокутний трикутник, у якого катети R та H, а гіпотенуза - . Картинки по запросу види трикутників

H Рис.8

H = 10 м, R = 10 м, тоді за теоремою Піфагора ,

(м), отже,

S_{бічна пов.} = ( м²).

S_{повна пов.} = S_{бічна пов.}+ S_основи; S_основи= ; S_основи= ( м²).

S_{повна пов.} = 444,063 + 314 = 758,063 ( м²).

Обчислимо відношення

Запишемо одержані результати у таблицю 1.

№	Форма будинку	Об’єм ( V ), м³	Площа повної поверхні (S_повна),м²	Співвідношення
1	Паралелепіпед	2000	1000	0,5
2	Піраміда	666,(6)	565,0282	0,85
3	Циліндр	3140	1256	0,4
4	Куля	523,(3)	314	0,6
5	Конус	1046,(6)	758,063	0,7

№	Форма будинку	Об’єм ( V ), м³	Площа повної поверхні (S_{повна ),}м²	Співвідношення
1	Паралелепіпед	600	580	0,9(6)
2	Піраміда	200	421,02	2,1
3	Циліндр	942	816,4	0,87
4	Куля	14,13	28,26	2
5	Конус	314	412,34	1,3

5. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

За результатами нашого дослідження можна зробити висновок, що найбільш вдалою формою для будування будинку із висотою 3 м є циліндр та паралелепіпед, оскільки їх відношення площі до об’єму є найменші з одержаних у таблиці результатів.

Отже при збільшенні висоти будинку відбуваються зміни його пропорцій, тобто перелік та кількість фігур раціональних для будування можуть змінюватися та варіюватися. Таким чином, підвищення енергоефективності будинків залежить не лише від їх форм, але також від співвідношення площі зовнішніх огороджень до об’єму.

Далі викладач оцінює роботу учнів.

6. ДОМАШНЄ ЗАВДАННЯ

Завдання 1. Розв’язати задачу

Результат пошуку зображень за запитом "конусоподібний намет"

Конусоподібний намет висотою 3,5м і діаметром основи 4м покрито тканиною. Скільки тканини пішло на намет?

Дано: конус, SO = H = 3.5м, d = 4м.

Знайти: S_б

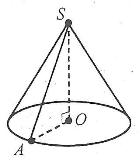
Розв’язання: S_б. = Результат пошуку зображень за запитом "конус"

З трикутника АОS: кут О = 90°, за т. Піфагора:

S_б = 3,14 · 2 · 4,03 =25,3 м².

Відповідь: 25,3 м² тканини пішло на намет.

Задача 2

Скільки мішків аміачної селітри можна помістити в склад розмірами 20м х 9м х 4м, якщо мішок селітри можна прийняти (з певною похибкою) за прямокутний паралелепіпед розмірами 90смх 5смх25см? (На щілини між мішками і центральний прохід виділяється 30% об’єму складу) Результат пошуку зображень за запитом "мішки міндобрива у складу"