Розробка уроку з геометрії у 8 класі по темі "Чотирикутники"

Підсумковий урок по темі „Чотирикутники ”

Мета уроку: узагальнити та систематизувати знання учнів із теми „Чотирикутники ”. Удосконалити вміння та навички учнів застосувати набуті знання з теми під час розв’язування задач.

Тип уроку: застосування знань, умінь та навичок.

ХІД УРОКУ

І  ОРГАНІЗАЦІЙНИЙ МОМЕНТ 

ІІ  ОГОЛОШЕННЯ ТЕМИ, МЕТИ УРОКУ

Математика-дивовижна вчителька в мистецтві спрямовувати думки, наводити порядок там, де вони не впорядковані, фільтрувати брудне й наводити ясність.

                                                                                                                                             Ж.Фабр

Отже, на сьогоднішньому уроці ми повинні впорядкувати всі наші знання про геометричні фігури, які вивчили, узагальнити та систематизувати їх властивості; показати застосування цих властивостей під час розв’язування задач.

ІІІ АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

1.                Які геометричні фігури ми  вивчили?(Чотирикутник, паралелограм, прямокутник, ромб, квадрат, трапеція)

ЗАПИТАННЯ

1.Назвіть усі властивості, які має паралелограм.

1)Протилежні сторони паралельні(за означенням).

2)Протилежні сторони рівні.

3)Протилежні кути рівні.

4)Діагоналі перетинаються і в точці перетину діляться навпіл.

5)Сума кутів, прилеглих до однієї сторони, дорівнює 180⁰.

2.Назвіть додаткові властивості прямокутника.

1)Усі кути прямі (за означенням).

2)Діагоналі рівні.

3.Назвіть додаткові властивості ромба.

1)Усі сторони рівні(за означенням).

2)Діагоналі перетинаються під прямим кутом і є бісектрисами його кутів.

4.                            Назвіть додаткові властивості квадрата.

Усі властивості паралелограма + властивості прямокутника + властивості ромба)

ІV ЗАСТОСУВАННЯ ЗНАНЬ, УМІНЬ, НАВИЧОК

Усне розв’язування задач.

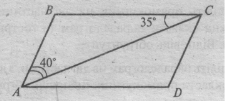
Задача 1. ABCD – паралелограм. Знайти: кути паралелограма.

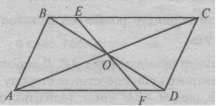
Задача 2. ABCD – паралелограм. Довести: OE=OF.

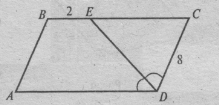
Задача 3. ABCD – паралелограм. Знайти: Р_ABCD.

Задача 4. ABCD – паралелограм. Знайти: кути паралелограма.

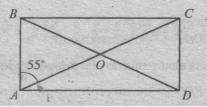
Задача 5. ABCD – прямокутник. Знайти: кути трикутника COD і трикутника ACB.

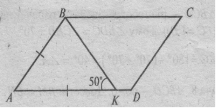
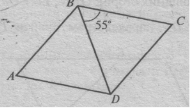
Задача 6. ABCD – ромб. Знайти: кут BAD.

Письмове розв'язування задач.

Клас ділиться на 5 команд. Кожна команда отримує своє завдання. На виконання завдання відводиться 8 хв.

1 команда. Знайдіть меншу бічну сторону прямокутної трапеції, якщо її основи дорівнюють 4 см і 7 см, а один із кутів дорівнює 135⁰.

2 команда.  Бісектриси кутів А і D паралелограма АВСD ділять сторону ВС на три рівних частини. Знайдіть сторони паралелограма, якщо його периметр дорівнює 70 см.

3 команда.  Знайти кути ромба, якщо його сторона утворює з діагоналями кути, які відносяться як 7 : 8.

4 команда.  З вершини В тупого кута ромба АВСD проведено висоти ВК і ВМ. Відомо, що КМ = ВК. Знайти кути ромба.

5 команда.  У прямокутнику ABCD AE і CF – перпендикуляри, що проведені з вершин А та С на діагональ BD. Кут між діагоналями дорівнює 30⁰, CF =2 см. Знайти довжину діагоналі BD.

Виконання практичного завдання.

1. Розділіть прямокутник на дві частини, з яких можна скласти паралелограм (з гострим кутом 45⁰). Відповідь обгрунтуйте.

2. Поділіть паралелограм на дві частини, з яких можна скласти прямокутник. Відповідь обгрунтуйте.

V ПІДБИТТЯ ПІДСУМКІВ УРОКУ

У вигляді презентацій: підготували учні класу.

ПРЕЗЕНТАЦІЯ ПРЯМОКУТНИКА

Я - прямокутник, тобто паралелограм, у якого всі кути прямі. У мене протилежні сторони рівні, діагоналі в точці перетину діляться навпіл. Ще мене діагональ ділить на два рівні трикутники. Також, мої діагоналі рівні, і вони ділять мене на чотири рівнобедрені трикутники.

ПРЕЗЕНТАЦІЯ РОМБА

Я - ромб, тобто паралелограм, у якого всі сторони рівні.

У мене:

- протилежні кути рівні;

- сума кутів прилеглих до однієї сторони дорівнює 180⁰;

- діагоналі в точці перетину діляться навпіл;

- в мене можна вписати коло.

ПРЕЗЕНТАЦІЯ  ТРАПЕЦІЇ

Я – трапеція. У  мене  дві  протилежні  сторони  паралельні, а  дві  не  паралельні. Паралельні  сторони  називають  основами, а непаралельні – бічними  сторонами. Моя  середня  лінія  паралельна  до  кожної  з  основ  і  дорівнює  їх  півсумі.

     Сума  кутів, що  прилягають  до  бічної  сторони, дорівнює  180⁰.

     Якщо в мене  є  один  прямий  кут, мене називають  прямокутною. Якщо в мене бічні  сторони  рівні  я – рівнобічна.        Якщо  я  рівнобічна,  то  мої  діагоналі  рівні, кути  при  будь – якій з  основ  також  рівні.              

ПРЕЗЕНТАЦІЯ КВАДРАТА

Я - квадрат, тобто прямокутник, у якого всі сторони рівні. У мене діагоналі перетинаються під прямим кутом і діагональ є бісектрисою кута. Ще я маю чотири кута, які є прямими. А якщо у мене провести діагоналі, то вони будуть рівними.

ПРЕЗЕНТАЦІЯ ПАРАЛЕЛОГРАМА

Я – паралелограм, тобто чотирикутник, у якого протилежні сторони попарно паралельні. У мене протилежні кути рівні, а сума кутів прилеглих до однієї сторони дорівнює 180⁰. Діагональ ділить мене на два рівні трикутники. Мої протилежні сторони рівні. Мої діагоналі в точці перетину діляться навпіл.

VІ ПОВІДОМЛЕННЯ ДОМАШНЬОГО ЗАВДАННЯ

Підручник Г. В. Апостолової.

1.                Повторити параграфи 12, 15, 16.
2.                Виконати вправи №11,12 (ст.102), №4 (ст. 92), №4(а,б) (ст.75)

ВИКОРИСТАНА ЛІТЕРАТУРА

1.                Журнал „Математика в школах України”, № 25-26
2.                Інтерактивні технології на уроках математики/ Уклад. І.С. Маркова.– Х.: Вид. група „Основа”, 2009. – 126 с.
3.                Г.В. Апостолова. Геометрія: 9: дворів. підруч. для загальноосвіт. навч. закл. – К.: Генеза, 2009. – 304 с.: іл.