Урок "Чотирикутники"

 

 

 

 

 

 

 

 

 

 

УРОК  ГЕОМЕТРІЇ 

 8  КЛАС

ТЕМА. ЧОТИРИКУТНИКИ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА. ЧОТИРИКУТНИКИ.

ТИП  УРОКУ:  ПІДСУМКОВИЙ з застосуванням інтерактивних технологій.

МЕТА :

1. Повторити, систематизувати та узагальнити знання  учнів щодо змісту:
   • властивості та ознаки чотирикутників: паралелограма, прямокутника, ромба, квадрата, трапеції;
   • теореми Фалеса;
   • означення та властивостей вписаних та центральних кутів;
   • означення та властивостей середньої лінії трикутника і трапеції;
   • перевірити  ці  знання  та  вміння  застосовувати  їх  при  розв’язуванні  задач, вирішенні  практичних  завдань;

формування предметних компетентностей: повторити, закріпити, розвинути та вдосконалити навики застосовувати  властивості та ознаки чотирикутників; розвивати увагу, критичне мислення, пам'ять, вміння спілкуватись, аналізувати ситуацію, допомагати іншим, вміння застосовувати набуті знання в життєвих ситуаціях;

формувати потребу до постійної самоосвіти, продуктивної творчої діяльності; створити умови для виховання культури навчальної праці, організованості, відповідальності, посилювати міжпредметну інтеграцію.

формування ключових компетентностей: спілкування державною мовою, математична компетентність, інформаційно-цифрова, уміння вчитися впродовж життя, полікультурна компетентність.

    ОБЛАДНАННЯ : таблиці  з  чотирикутниками, українськими  прислів'ями, електронні засоби навчання: комп’ютерна презентація з даної теми, Інтернет-гра «Танграм», кросворд,  таблиці контролю, тести в електронному варіанті.

 

 Організаційний момент

Відомий педагог В.О.Сухомлинський одного разу зауважив: «Знати – це означає, насамперед,  уміти користуватися знаннями».

Ці слова ми візьмемо за епіграф нашого уроку, на якому ви не просто зможете пригадати матеріал з теми «Чотирикутники», але й цікаво, я сподіваюсь, проведете час. Сьогодні у нас урок-подорож по країні «Чотирикутники». Щоб подорож була цікавою, успішною, ви повинні показати всі знання з даної теми. Під час подорожі бажаю вам  виявити свою самостійність, показати свої знання, творчі здібності. Діти, ми будемо разом з вами подорожувати на кораблі, який назвемо «Дружба», оскільки працюватимете ви по групах, тобто кают-компаніях. (Обираються керівники груп). Ви зможете сьогодні дати оцінку один одному і самому собі. У кожної групи є лист оцінювання, де ви будете зазначати бали за кожен вид роботи.

І. Актуалізація  опорних  знань.

Девіз: „Знання  збираються  по  краплині, як  вода  в  долині”.

Отже, ми розпочинаємо нашу подорож. Відкрийте свої бортові журнали і зробіть перший запис (дата і тема уроку).

Ось ми наближаємось до порту «Паралелограм». Але для того, щоб потрапити сюди, потрібно згадати основні властивості чотирикутників. Дане завдання ми проведемо у формі відомої гри «Доміно».

Правила гри: У кожного учня є картка, що містить запитання і відповідь. Починає гру учень з картками, у яких позначені слова «Старт» і «Фініш». Він ставить стартове запитання і закінчує гру фінішною відповіддю. Кожен учень уважно стежить за ходом гри, щоб не пропустити свою відповідь.

Запитання до гри

Старт

Яка фігура називається чотирикутником?

Багатокутник, що має 4 вершини, 4 сторони і 2 діагоналі.                                                           Як називаються дві несуміжні сторони чотирикутника?

Протилежні.

Які вершини чотирикутника називаються протилежними?

Дві вершини, що не є сусідніми.

Чому дорівнює сума кутів опуклого чотирикутника

360°

Що називається паралелограмом?

Чотирикутник, у якого протилежні сторони попарно паралельні. Чи є паралелограм опуклим чотирикутником?

Є.

Що таке трапеція?

Чотирикутник, у якого дві сторони паралельні, а дві інші сторони непаралельні.

Що називається основами трапеції?

 

Паралельні сторони трапеції.

Як називаються непаралельні сторони трапеції?

Бічними сторонами.

Яка трапеція називається рівнобедреною?

Трапеція, у якої бічні сторони рівні.

Як називається трапеція, у якої один з кутів прямий?

Паралелограм, у якого всі сторони рівні.

Що називається квадратом?

Прямокутник, у якого всі сторони рівні
Назвіть властивості квадрата.

Усі кути прямі, діагоналі рівні, діагоналі перетинаються під прямим кутом і є бісектрисами кутів.

Назвіть одну з ознак паралелограма.

У чотирикутнику дві сторони рівні і паралельні. Назвіть властивість діагоналей прямокутника.

Діагоналі рівні.

Сформулюйте теорему Фалеса.

Якщо паралельні прямі, що перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на іншій його стороні.

Що називаються середньою лінією трапеції.

Відрізок, що з'єднує середини бічних сторін.

Фініш

Так, я бачу, що ви пам’ятаєте властивості чотирикутників і хочу задати вам ще ось такі запитання:

1. Сформулюйте означення прямокутника через чотирикутник.
2. …квадрата через ромб.
3. …ромба через чотирикутник.
4. …квадрата через паралелограм.
5. …прямокутника через паралелограм.
6. …квадрата через чотирикутник.
7. …ромба через паралелограм.

 

Прошу командирів груп оцінити роботу учасників вашої групи за дане завдання.

 

ІІ. Відпрацювання  навичок.

Наша подорож продовжується. Наступна зупинка «Ромб»

 

Девіз: „Один  розум  добре, а  декілька – краще”.

ІІІ. Розв'язування  вправ.

ДЕВІЗ  : „ Якщо  не  висловлено  різні  думки,  немає  з  чого  вибирати  краще”.

Учням пропонується для двох задач висловити думки щодо плану розв’язування задач, а третю задачу розв’язати повністю на дошці.

Задача 1.

Основи NK i MP рівнобічної трапеції MNKP відповідно дорівнюють 4 см і 11 см. Знайти периметр трапеції, якщо діагональ МК є бісектрисою кута М.

 

Задача 2.

Знайти гострі кути прямокутного трикутника, вписаного в коло, якщо дуги, на які вони спираються, відносяться як 8:10.

Задача 3.

Коло, вписане в прямокутну трапецію, ділить точкою дотику більшу бічну сторону на відрізки завдовжки 8 см і 50 см. Знайдіть периметр даної трапеції, якщо радіус вписаного кола дорівнює 20 см.

 

 

ІV. Закріплення  знань  та  застосування  їх  на  практиці.

Девіз : „Не  досить  оволодіти  премудрістю, потрібно  також  вміти  користуватися  нею”.

 

1. Практична  робота.

1. Користуючись  вивченими  властивостями, визначити  центр  чотирикутника, вирізаного з  паперу ( учням  роздаються  паперові  паралелограми,  квадрати, ромби, прямокутники).

 

2)  Щоб  вирізати  прямокутник  з   аркушу  картону, який  має  вигляд  чотирикутника  неправильної  форми, тесля  провів  його  діагоналі  і  від  точки  перетину  цих  діагоналей  в  різні  сторони  по  ним  відклав  відрізки  однакової  довжини, а  потім  послідовно  з'єднав  кінці  цих  відрізків. Чи  вірно  це?

3)    Майстер-паркетник хоче пересвідчитись, що випиляні з дуба чотирикутники – квадрати. Чи достатньо для цього:

a.    Рівності чотирьох сторін? (ні, може бути ромб);

b.    Рівності обох діагоналей? (ні може бути прямокутник);

c.    Рівності чотирьох відрізків поділу діагоналей? (ні може бути прямокутник);

d.    Рівності діагоналі і прямого кута між ними? (ні може бути рівнобедрена трапеція);

(достатньо, наприклад, одночасної рівності сторін і рівності діагоналей).

4)    Швачка хоче переконатися, що виготовлена нею серветка квадратна. Чи досить для цього:

a.    Двічі перегнути її по діагоналі, слідкуючи, щоб збігалися при цьому сторони?

 (ні може бути ромб);

b.    Двічі перегнути її по „середніх „лініях, досягаючи суміщення протилежних сторін? (ні може бути прямокутник);

c.    Спочатку перегнути її по діагоналі, а тоді сумістити кінці цієї діагоналі?

 (ні може бути ромб);

d.    Двічі перегнути її по діагоналі, щоб співпадали утворені трикутники?

 (ні може бути ромб);

(потрібно одночасно перегнути і по „середній” лінії).

 

V. Перевірка  знань  кожного  учня.

 

Девіз: „Живи  своїм  розумом, але  звіряйся  з  чужим”.

 

 

1. Тестування.

 

Виконання тестових завдань із наступною взаємоперевіркою

Варіант І

1. Одна із сторін паралелограма в 4 рази більша від іншої, а пери­
   метр становить 30 см. Чому дорівнюють сторони паралелограма?

а) 4 см, 4 см, 16 см, 16 см;

б) 6 см, 24 см, 6 см, 24 см;

в) 3 см, 12 см, 3 см, 12 см.

2. Знайдіть кути паралелограма, якщо відомо, що один з них біль­ший від іншого на 50°.

а)   70°, 120°; б) 115°, 65°; в) 125°, 75°.

3. Знайдіть периметр ромба ABCD, якщо відомо, що довжина його меншої діагоналі АС дорівнює 4 см, а тупий кут дорівнює 120°.

а)   64 см; б) 20 см; в) 16 см.

4. Сторона ромба дорівнює 5 м, а його менша діагональ — 6 м. Знайдіть більшу діагональ.

а) 10 м; б) 12 м; в) 8 м.

5. Діагональ ромба утворює з однією з його сторін кут 25°. Знайдіть більший кут ромба.

а)   100°; б) 130°; в) 50°.

6. Знайдіть сторону квадрата, діагональ якого дорівнює 10 см.
   а) 100 см; б) 5см; в) 5 см.
7. Бісектриси кутів прямокутника перетинаються в точках М, N, Р, К. Вершинами якого чотирикутника є ці точки?

а) Ромба; б) прямокутника;    в) квадрата.

8. Сторони прямокутника дорівнюють 6 см і 8 см. Знайдіть його діагоналі.

а) 10 см; б) 14 см; в) 20 см.

9. Бічна сторона рівнобічної трапеції дорівнює 8 см, а середня лі­нія — 10 см. Знайдіть периметр трапеції.

а) 20 см; б) 16 см; в) 18 см; г) 36 см.

10. У рівнобічній трапеції гострі кути дорівнюють 60°, бічна сторона дорівнює 10 см, а більша основа — 15 см. Знайдіть меншу основу
    та середню лінію трапеції.

а) 10 см, 12,5 см;      б) 5 см, 10 см; в) 15 см, 30 см.

11. У колі проведені діаметри АС і BD. Визначте вид чотирикутника ABCD.

а) Паралелограм;  б) ромб; в) прямокутник.

12.  За рис. 21 знайдіть кут х, якщо точка О — центр кола,      α = 21°, β = 49°.
    а)   20°; б) 40°; в) 42°.

 

Варіант II

1. Одна із сторін паралелограма на 10 см більша від іншої, а пери­метр становить 68 см. Знайдіть довжини сторін паралелограма.

а) 10 см, 10 см, 22 см, 22 см;

б) 22 см, 22 см, 12 см, 12 см;

в) 10 см, 10 см, 12 см, 12 см.

2. Знайдіть кути паралелограма, якщо відомо, що один з них менший від іншого на 40°.

а) 120°, 80°; б) 130°, 90°; в) 110°, 70°.

3. Знайдіть периметр ромба ABCD, якщо менша діагональ АС дорівнює 5 дм, а кут між нею та стороною дорівнює 60°.

а) 64 дм; б) 20 дм; в) 16 дм.

4. Діагоналі ромба дорівнюють 12 м і 16 м. Знайдіть сторону ромба.

 а) 10 м; б) 12 м; в) 16 м.

5. Діагональ ромба дорівнює його стороні. Знайдіть більший кут ромба.

а) 120°; б) 100°; в) 60°.

6. Сторона квадрата дорівнює 10 см. Знайдіть його діагональ.

а) 10 см; б) 10 см; в) 5 см.

7. Бісектриси кутів паралелограма перетинаються в точках N, Р, О, К. Вершинами якого чотирикутника є ці точки?

а) Паралелограма;  б) прямокутника;  в) ромба.

8. Знайдіть периметр прямокутника, якщо одна з його сторін до­рівнює 5 см, а діагональ — 13 см.

а) 17 см; б) 26 см; в) 34 см.

9. Периметр рівнобічної трапеції становить 36 см, а середня лінія трапеції дорівнює 10 см. Знайдіть її бічну сторону.

а) 26 см; б) 20 см; в) 16 см; г) 8 см.

10. У рівнобічній трапеції МНКР до більшої основи MP проведений
    перпендикуляр НЕ, ME = 6 см, НК = 10 см. Знайдіть більшу основу й середню лінію трапеції.

а) 32 см, 22 см; б) 22 см, 16 см;       в) 16 см, 32 см.

11. У колі діаметри MN і KF перетинаються під кутом 60°. Знай­діть меншу сторону чотирикутника MNKF, якщо діаметр кола дорівнює 10 см.

а) 15 см; б) 5 см; в) 3,5 см.

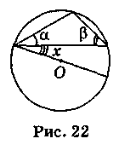
12. За рис. 22 знайдіть кут х, якщо точка О — центр кола,     α = 19°, β = 47°.

а) 48°; б) 24°; в) 38°.

УІ. Підсумок  уроку.

Учні  відповідають  на  запитання  вчителя:

• Що  цікавого  дізналися  ви  сьогодні  на  уроці?
• Що  сподобалося  найбільше?
• Які були труднощі?
• Над чим треба ще попрацювати вдома?

 

Учні:

-сьогодні на уроці я навчився…

-сьогодні на уроці я запам’ятав…

-сьогодні на уроці я повторив…

 

 

Завдання  додому:

 

……

 

Підготуватися  до  контрольної  роботи.