Розробка уроку з математики на тему:Формула коренів квадратного рівняння

Тема. Формула коренів квадратного рівняння

Мета: домогтися засвоєння учнями змісту поняття «дискримінант квадратного рівняння», формули дискримінанта та схеми виводу формул для розв’язування квадратного рівняння загального вигляду, а також формул коренів квадратного рівняння; сформувати первинні вміння знаходити за формулами дискримінант квадратного рівняння, за його значенням визначати кількість розв’язків квадратного рівняння й обчислювати корені квадратного рівняння; розвивати знання про квадратні рівняння та логічне мислення; виховувати в учнів охайність в записах, вміння аналізувати та логічно висловлювати  свої думки.

Тип уроку: засвоєння нових знань.

Обладнання:презентація,  таблиця, роздатковий матеріал

При розв’язанні рівнянь ми пізнаємо навколишній світ

(Александров)

Хід уроку

І. Організаційний момент

   З’ясувати емоційний стан учнів класу ( за допомогою сигнальних карток).

ІІ. Перевірка домашнього завдання

1. По одному учню розв’язують  рівняння( № 5 – 8 – розклавши його ліву частину на множники)  і по черзі записують літеру.

1) + 7х = 0;                                    5) – 10х + 9 = 0;

2) 2 – 11х = 0;                               6) + 2х – 3 = 0;

3) 3 – 6 = 0;                                    7) – х – 2 = 0;

4) 8 = 0;                                          8) + 6х + 5 = 0.

Ш: -7 і 0;  Е: 0 і 5,5; В: - і ; Ч: 0; Е: 1 і 9; Н: -3 і 1; К: -1 і 2;  О: -5 і -1.

2. 1.Метод « Світлофор»

- що називається квадратним рівнянням?

- як називаються коефіцієнти рівняння?

- яке рівняння називається зведеним?

- яке рівняння називається неповним?

 

ІІІ. Формулювання мети і завдань уроку

    В домашньому завданні ви зустрічалися із зведеними квадратними рівняннями, де треба розкласти його ліву частину на множники, але якщо у вас зустрінуться рівняння, які не є зведеними, необхідно знайти достатньо простий алгоритм розв’язування квадратних рівнянь загального вигляду. Розв’язання цієї проблеми і є головною метою нашого уроку.

Повторення правил роботи на уроці.( Говорять всі разом)

Аутотренінг

Схиліть голівки на руки, заплющте оченята. Подумки повторюйте за мною:

Я прийшов до школи вчитися… У мене все вийде…

Треба бути уважним…

Треба бути спокійним…

В класі у мене друзі…

Вони мене люблять…

Мені приємно…

 Я легко дихаю…

Люблю я свій розум… увагу і пам'ять.

Працює мій мозок,

І вчусь я старанно, сприймаю все нове

І мислю логічно. Вчителя слово

Здійсню я практично

 

. Актуалізація опорних знань та вмінь

   З метою успішного сприйняття учнями навчального матеріалу перед його вивченням слід активізувати такі знання і вміння учнів.

Усно.

1. Розв’язати рівняння:

а) = 25; б) 4= 14; в) = 0.

2. Замініть рівняння рівносильним зведеним квадратним рівнянням:

а) 2- 6х + 10 = 0; б) 3 – 12х + 3 = 0; в) -+х – 7 = 0.

3. Подати тричлен у вигляді квадрата двочлена

а) + 2х +1; б) - 2х + 1; в) + 6х + 9; г) + 12х + 36.

V. Засвоєння знань

1. Виведення формул

    Виведемо формулу, яка дає змогу за коефіцієнтами а, в, с квадратного рівняння а+ вх + с = 0 знаходити його корені. Маємо:  а+ вх + с = 0. Оскільки а0, то, помноживши обидві частини цього рівняння на 4а, отримаємо рівняння, рівносильне даному: 4+4авх + 4ас = 0.

Виділимо в лівій частині  цього рівняння квадрат двочлена: 4+4авх + 4ас = 0;

= – 4ас.

  Існування коренів рівняння = – 4ас та їх кількість залежить від знака виразу – 4ас.

Цей вираз називають дискримінантом квадратного рівняння а+ вх + с = 0 і позначають буквою Д, тобто Д = – 4ас. Термін «дискримінант» походить від латинського слова discriminare, що означає «розрізняти», «розділяти».

Тепер рівняння = – 4ас можна записати так: = Д.

Можливі три випадки: Д0, Д = 0, Д0.

1. Якщо  Д0, то рівняння а+ вх + с = 0 коренів не має. Справді, при будь-якому значенні х вираз

набуває тільки невід’ємних значень.

Висновок: якщо Д0, то квадратне рівняння а+ вх + с = 0 коренів не має.

2. Якщо Д = 0, то рівняння  = Д набуває вигляду: = 0. Звідси 2ах + в = 0;

 х = -.

Висновок:  : якщо Д0, то квадратне рівняння а+ вх + с = 0 має один корінь х = -.

3. Якщо  Д0, то рівняння = Д можна записати у вигляді:  = .

Звідси 2ах + в = - або 2ах + в = . тоді х = або х = .

Висновок:  . Якщо  Д0, то квадратне  рівняння  має два корені  = або = .

Також застосовують коротку форму запису: х = .

Цей запис називають формулою коренів квадратного рівняння  а+ вх + с = 0.

   Отриману формулу можна застосувати і для випадку, коли Д = 0. Тоді

 х = = - .

Австралійський дощ»

Ведучий запитує в учасників: «Чи знаєте ви, що таке австралійський дощ? Ні? Тоді давайте разом послухаємо, який він. Зараз по колу ланцюжком ви будете передавати мої рухи. Як тільки вони повернуться до мене, я передам наступні. Слідкуйте уважно».

-         В Австралії піднявся вітер. (Ведучий тре долоні)

•   Падають перші краплини дощу (клацаємо пальцями).

•Почалася злива (плескаємо долонями по стегнам).

•Ось буря стихає (плескаємо долонями по грудині).

•Стихає злива (плескаємо долонями по стегнам).

•Закінчується дощ, падають останні краплі (клацаємо пальцями).

• Шумить тільки вітер (потираємо долоні).

•Австралійський дощ скінчився. Сонце! (Діти піднімають руки вгору)

   При  розв’язуванні квадратних рівнянь зручно керуватися таким алгоритмом:

• знайти дискримінант Д квадратного рівняння;
• якщо  Д0, то у відповіді записати, що коренів немає;
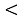
• якщо Д0, то скористатися формулою коренів квадратного рівняння.

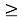
2. Приклад.

Розв’яжіть рівняння: 3- 2х – 16 = 0.

Розв’язання

Для даного рівняння а= 3, в= -2, с= -16.

Дискримінант рівняння Д= = – 4ас= - 43 ( -16) = 4 + 192 = 196.

Отже, = = = - 2, = = = 2.

Відповідь: -2;  2.

VІ. Формування вмінь

№1. Знайшовши дискримінант квадратного рівняння та визначивши кількість коренів цього рівняння,  з’ясуємо роки життя   Т.Г. Шевченка:

а) 2 – 3х + 1 = 0; б)4+ 4х + 1 = 0; в) -3+ 6х – 4 = 0; г) 2+ 3х + 1 = 0; д) 9+ 6х + 1 = 0;

е) + 5х – 6 = 0; є) 5+ 3х + 2 = 0; ж) 2- 3х – 5 = 0.

Відповіді: а) 1: Д =1; б) 8: Д =0; в) 1: Д = -12; г) 4 :Д =  1; д) 1: Д = 0; е) 8: Д = 49; є) 6: Д = - 31;

 ж) 1: Д = 49.

Так, незабаром, 9 березня все прогресивне людство буде святкувати день народження Т.Г. Шевченка.

№2. Розв’язавши квадратне рівняння ми будемо знати, який збірник Т.Г. Шевченка був початком періоду в історії української літератури:

а) 2- 5х + 3 = 0; б) 2+ х – 1 = 0; в) 3+ 5х – 2 = 0; г) 4- 4х + 1 = 0; д) 2- 3х + 2 = 0;

е) 7- 6х – 1 = 0

К: 1 і 1,5; О: -1 і 0,5; Б: -1 і -; З: 0,5; А: коренів немає; Р: і .

                                Кобзарем його ми звемо

                                                              Так від роду і до роду

                                                               Кожен вірш свій і поему.

                                                               Він присвячує народу

                                                                                      ( М. Рильський)

№3. Логічні вправи та завдання підвищеного рівня складності для учнів.

Розв’язавши дані вправи, ви зможете дізнатися які твори Т.Г. Шевченка ви вивчаєте у 8 класі.

    1) Знайдіть значення в, при якому один із коренів рівняння дорівнює -3.

    а)20+ вх – в = 0;  б) - вх – 14 = 0.

     2) Вставте пропущений вираз: ( 2- ) (2+ ) = ?

Відповідь: Думи: -15 і 12    мої : -16  і 4        думи мої: 4- в.

Прочитати 4 рядки даного вірша.

№ 4. Робота в мікро групах.

    Виконавши правильно дані завдання, ви зможете з’ясувати рік написання даного твору

1) Обчислити дискримінант 3- 8х – 3 = 0;

2) Розв’язати рівняння - 8х – 9 = 0;

3) Скільки коренів має рівняння - 10х + 25 = 0;

4) За якої умови дане повне квадратне  рівняння не має дійсних коренів?

Відповіді: 1: Д = 100; 8: -1 і 9; 3: один; 9: Д0.

 

В сім‘ї великій,

                  У цвіту садів прекрасних

          Буде жити він вовіки,

                         Як безсмертний наш сучасник!

V. Закріплення вивченого матеріалу

Метод « Математичне фехтування»

Учні задають один одному запитання

 

 

 

 

 

Метод « Фіш- боун»

 

 

 

 

 

 

 

VІІ. Підсумки уроку

Метод « Лепбук»

1. Що ви дізналися сьогодні на уроці?

2. Чому навчилися?

3. Що вам сподобалося на уроці?

4. Що запам’яталося?

VІІІ. Домашнє завдання

Вивчити теоретичний матеріал, розв’язати рівняння:

№1   б)

        в)      г) .

№ 2  а)   б) +.

 Додатковий № 3

 а) 3.