Розробка уроку з математики у 6 класі на тему "Задачі на ділення дробів. Знаходження числа за його дробом"
Тема. Задачі на ділення дробів. Знаходження числа за його дробом
Мета: домогтися засвоєння учнями алгоритму розв'язування задач на знаходження числа за його дробом (відсотками); повторити алгоритми розв'язування інших задач на ділення; виробляти вміння розв'язувати задачі на застосування названих алгоритмів.
Тип уроку: засвоєння знань та вмінь.
Хід уроку
І. Актуалізація опорних знань
Усні вправи
-
Виконайте ділення:
 ;
; 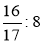 ;
; 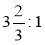 ;
;  ;
;  .
.
-
Розв'яжіть рівняння:
 ;
;  ;
;  ;
; 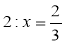 ;
; 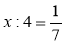 .
.
-
Відрізок довжиною
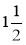 дм розділити на 3 рівних частини. Чому дорівнює довжина однієї частини?
дм розділити на 3 рівних частини. Чому дорівнює довжина однієї частини?
-
Знайдіть швидкість пішохода, якщо шлях у 5 км він долає за
 години.
години.
-
Дане число збільшили у
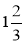 раза і дістали
раза і дістали 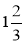 . Яке було число до збільшення?
. Яке було число до збільшення?
-
Як знайти
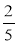 від 2000 м2? 40 % від 2000 м2?
від 2000 м2? 40 % від 2000 м2?
-
Виразіть дробом (десятковим або звичайним): 50 %; 3 %; 25 %; 37 %;
137%; 180%;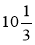 %.
%.
II. Систематизація знань. Мотивація діяльності
Після розв'язування усних вправ (№ 3, 4, 5) робимо висновок: з деякими видами задач на ділення ми знайомі (1) задача на знаходження швидкості руху за відомим часом і відстанню; 2) знаходження числа, яке менше від даного у ![]() разів; 3) також задачі на знаходження частки від ділення цілого на кілька рівних частин та ін.); але є ще один вид задач, що розв'язуються діленням.
разів; 3) також задачі на знаходження частки від ділення цілого на кілька рівних частин та ін.); але є ще один вид задач, що розв'язуються діленням.
III. Засвоєння знань (фронтальна робота)
-
Задача. Розчистили від снігу
 ковзанки, що становить 800 м2. Знайдіть площу ковзанки.
ковзанки, що становить 800 м2. Знайдіть площу ковзанки.
Розв'язання. Нехай площа ковзанки х м2.
За умовою ![]() від х (м) дорівнює 800 м2. (*)
від х (м) дорівнює 800 м2. (*)
Отже, ![]() · х = 800, тобто х = 800 :
· х = 800, тобто х = 800 : ![]() . (**); х = 800 ·
. (**); х = 800 · ![]() = 2000.
= 2000.
Відповідь. Площа ковзанки 2000 м2.
Порівнявши (*) і (**), робимо висновок:
Щоб знайти число за даним значенням його дробу, треба це значення поділити на дріб.
Для «сильних» учнів цей матеріал можна записати у вигляді формули.
Якщо ![]() від х становить с, х = с :
від х становить с, х = с : ![]() .
.
Приклад
- Задача. Житом засіяно 2 400 га, що становить 0,8 усього поля. Знайдіть площу поля.
Розв'язання. Оскільки відомо, що 0,8 від (х) поля становить 2 400 га,
то х = 2400 : 0,8 = 3000 га.
- Задача. Маса сушеної риби становить 55 % маси свіжої риби. Скільки треба взяти свіжої риби, щоб дістати 231 кг сушеної риби.
Розв'язання. Зрозуміло, що треба знайти х, якщо 55 % від х становить 231 кг.
Задача відрізняється від задачі в п.1 тільки величиною «55 %». Але ж
55 % = 0,55, тому.
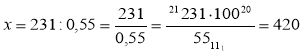 (кг).
(кг).
Висновок. Щоб знайти число за значенням його відсотків, треба:
- записати відсотки дробом;
- поділити значення відсотків на цей дріб.
Приклад
Збільшивши продуктивність праці на 7 %, робітник виконав за той самий час на 98 деталей більше, ніж було заплановано. Скільки деталей повинен був виготовити робітник за планом?
Розв'язання. 7 % = 0,07; 98 : 0,07 = 1 400.
Відповідь. За планом 1 400 деталей.
У зошитах маємо запис у вигляді конспекту 21.
|
|
Конспект 21 |
|
|
Знаходження числа за значенням його дробу (відсотків) |
||
|
Правило 1) Знайдіть х, якщо
2) Знайдіть х, якщо р % від х становить с: а) р % виражаємо у вигляді
б) х = с : |
Приклад
1) Знайдіть число, якщо
2) Знайдіть число, якщо 30 % його становить 90: а) 30% = 0,3; б) 90 : 0,3 = 300. |
|
IV. Засвоєння вмінь
Задачі такого типу, які розв'язуються на цьому уроці, вже зустрічалися учням (5 клас). Але, на відміну від вивченого раніше способу, подібні задачі ми повинні тепер навчитися розв'язувати діленням. Тому слід переконати учнів у тому, що розібраний на уроці спосіб є кращим, і вимагати від учнів знаходити число за його дробом (відсотками) тільки діленням!
І рівень
Усні вправи
-
На присадибній ділянці зібрали 8 кг огірків, що становить
 зібраних овочів. Скільки кілограмів овочів зібрали?
зібраних овочів. Скільки кілограмів овочів зібрали?
- На присадибній ділянці зібрали 8 кг огірків, що становить 0,4 зібраних овочів. Скільки кілограмів овочів зібрали?
- На присадибній ділянці зібрали 8 кг огірків, що становить 40 % зібраних овочів. Скільки кілограмів овочів зібрали?
II рівень
-
Який шлях пройде група туристів за 1 год, якщо
 км вона проходить за
км вона проходить за  год;
год; 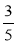 год;
год; 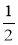 год?
год?
-
За
 м тканини заплатити 183 грн 75 к. Яка ціна одного метра тканини?
м тканини заплатити 183 грн 75 к. Яка ціна одного метра тканини?
-
Довжина земельної ділянки прямокутної форми 40 м, а ширина —
в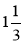 раза менша. Знайдіть площу ділянки.
раза менша. Знайдіть площу ділянки.
-
Одна сторона трикутника дорівнює
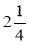 м, а друга і третя — відповідно
м, а друга і третя — відповідно
в і
і 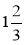 раза довші від першої. Знайдіть периметр трикутника.
раза довші від першої. Знайдіть периметр трикутника.
-
Знайдіть число: а)
 якого дорівнює 21; б)
якого дорівнює 21; б) 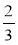 якого дорівнює 30; в) 0,7 якого дорівнює 14; г) 0,21 якого дорівнює 0,609.
якого дорівнює 30; в) 0,7 якого дорівнює 14; г) 0,21 якого дорівнює 0,609.
-
Кукурудзою засіяли 78 га поля, що становить
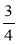 площі всього поля.
площі всього поля.
Яка площа всього поля? -
Знайдіть число: а) 15 % якого дорівнює 36; б)
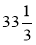 % якого дорівнює 41.
% якого дорівнює 41.
-
Із жита отримують 75% борошна. Скільки жита треба змолотити, щоб
отримати 60 кг борошна? -
Ширина пасовища прямокутної форми 30 м, що становить 48 % довжини. Яка площа пасовища? — Задачі на знаходження числа за його
дробом (відсотками).
Додатково (на повторення)
- Знайдіть значення виразу:
а) 8,45 · 9,6 – 7,8 · 8,45; б) 37,5 + (62,8 – 27,5): 4.
- а) 31,2 : х + 6,7, якщо х = 10; б) 38,5+ а : b, якщо а = 19,8, b = 90.
V. Підсумки уроку
Який з виразів є розв'язком задачі?
На лінію вийшло 56 автобусів, що становить ![]() усіх автобусів автопарку. Скільки автобусів у автопарку?
усіх автобусів автопарку. Скільки автобусів у автопарку?
1) ![]() · 56; 2)
· 56; 2) ![]() : 56; 3) 56 :
: 56; 3) 56 : ![]() ; 4) 56 +
; 4) 56 + ![]() .
.
VI. Домашнє завдання
-
Знайдіть число: а)
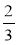 якого дорівнює 25; б)
якого дорівнює 25; б) 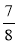 якого дорівнює
якого дорівнює  .
.
-
Автомат розфасовує желатин у пакетики по 0,03 кг. Скільки пакетиків
потрібно для розфасовки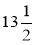 кг желатину?
кг желатину?
-
Велосипедист рухається зі швидкістю 21 км/год, що становить
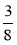 швидкості автомобіля. Яка швидкість автомобіля?
швидкості автомобіля. Яка швидкість автомобіля?
-
Знайдіть число: а) 35% якого дорівнює 7; б)
 % якого дорівнює 1,5.
% якого дорівнює 1,5.
-
У класі три відмінники, що становить 12 % усіх учнів класу. Скільки
учнів у класі?


про публікацію авторської розробки
Додати розробку
