Розробки уроків з теми «Інтеграл та його застосування» Профільний рівень. Методичні та дидактичні матеріали до 12 уроків теми.
Розробки уроків з теми «Інтеграл та його застосування» Профільний рівень. Методичні та дидактичні матеріали до 12 уроків теми.
Посібник складено відповідно до нової програми з алгебри 11 класу профільного рівня, побудовано з використанням форм і методів навчання, що відповідають специфіці курсу «Алгебра і початки аналізу», віковим особливостям учнів.
Збірник містить плани - конспекти до 12 уроків, у яких зазначено їхні основні структурні елементи та мету й завдання навчання, запропоновано комплекс диференційованих усних та письмових вправ, самостійних та контролюючих робіт, що супроводжуються розв'язаннями або відповідями.
У досвіді представлені уроки узагальнення та систематизації знань, контролю та корекції за допомогою електронних тестів.
З метою формування єдиної наукової картини світу, використано історичний матеріал, задачі прикладного змісту, простежується інтеграція з іншими науками.
Зміст посібника відповідає діючому підручнику А.Г.Мерзляк, Д.А.Номіровський Алгебра 11. Академічний та профільний рівні. Вид. Харків, Гімназія, 2011.
Призначено для вчителів математики .І.В.Брага

Усі уроки алгебри в 11 класі
з теми

І частина
Методичні та дидактичні
матеріали до 12 уроків
смт Губиниха-1, 2014
Автор: Брага Інна Вікторівна - вчитель вищої категорії, вчитель
Губиниської загальноосвітньої школи І- ІІІ ступеня №1
Рецензенти:
Конюхова Н.О.- заступник директора з НВР Губиниської ЗОШ І-ІІІ ступеня №1
Альошина Д.В.- вчитель вищої категорії Гвардійської ЗОШ І-ІІІ ступенів
Розробки уроків з теми «Інтеграл та його застосування» Профільний рівень. Методичні та дидактичні матеріали до 12 уроків теми.
Посібник складено відповідно до нової програми з алгебри 11 класу профільного рівня, побудовано з використанням форм і методів навчання, що відповідають специфіці курсу «Алгебра і початки аналізу», віковим особливостям учнів.
Збірник містить плани - конспекти до 12 уроків, у яких зазначено їхні основні структурні елементи та мету й завдання навчання, запропоновано комплекс диференційованих усних та письмових вправ, самостійних та контролюючих робіт, що супроводжуються розв’язаннями або відповідями.
У досвіді представлені уроки узагальнення та систематизації знань, контролю та корекції за допомогою електронних тестів.
З метою формування єдиної наукової картини світу, використано історичний матеріал, задачі прикладного змісту, простежується інтеграція з іншими науками.
Зміст посібника відповідає діючому підручнику А.Г.Мерзляк, Д.А.Номіровський Алгебра 11. Академічний та профільний рівні. Вид. Харків, Гімназія, 2011.
Призначено для вчителів математики .
Зміст
Урок 1. Первісна. Основна властивість первісної. Невизначений інтеграл…….......стр. 1
Урок 2. Розв’язування вправ (Первісна. Основна Властивість первісної. Невизначенийінтегра)………………………………………………………………………………………………… стр. 3
Урок 3. Правила знаходження первісної ………………………………………………………………..стр. 5
Урок 4.Розв’язування вправ. Урок- практикум ……………………………………………………. стр.8
Урок 5. Розв’язування вправ. Самостійна робота………………………………………………… стр.10
Урок 6. Розв’язування вправ…………….…………………………………………………………………….стр.11
Урок 7.Геометричний зміст та означення визначеного інтегралу. Формула Ньютона-Лейбніца……………………………………………………………………………………………………………………..стр.13
Урок 8.Розв’язування вправ…………………………………………………………………………………….стр.17
Урок 9. Роз’язування вправ «Первісна та інтеграл»………………………………………………стр.20
Урок 10. Розв’язування вправ «Первісна та інтеграл»………………………………………….стр.22
Урок 11. Контрольна робота «Первісна та інтеграл»…………………………………………….стр.23
Урок 12. Аналіз контрольних робіт. Розв’язування вправ…………………………………..стр.24
Література………………………………………………………………………………………………………………стр.25
Урок 1 . Тема. Первісна. Основна властивість первісної. Невизначений інтеграл.
Цілепокладання: на прикладі задач, що приводять до поняття первісної для функції, сформулювати поняття первісної для функції, сформувати поняття первісної для функції, домогтися усвідомлення учнями означення первісної, познайомити із основною властивістю первісної, дати означення невизначеного інтегралу; сформувати вміння визначати, чи є функція первісною для заданої функції; ознайомити з таблицею первісних та її застосуванням для знаходження первісних та обчислення невизначених інтегралів; вчити знаходити одну з первісних для заданої функції.
Розвивати пізнавальні можливості учнів, уміння аналізувати, робити висновки, знаходити способи розв’язування вправ.
Виховувати активність мислення, наполегливість у досягненні мети.
Очікуванні результати: учні розуміють поняття первісної та знають її основну властивість; встановлюють, чи є функція первісною для заданої функції; знаходять первісні та невизначені інтеграли із застосуванням таблиці первісних.
Обладнання: підручник, малюнки до основної властивості первісної (Використання комп’ютера, слайдів), таблиця первісних.
Тип уроку: засвоєння нових знань.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1. Вправа на повторення №6.7, ст52 та її самоперевірка за зразком на дошці.
Задача №6.7. Матеріальна точка рухається по координатній прямій за законом s(t)=2x2+3 (переміщення вимірюється в метрах, час в секундах) . Знайдіть миттєву швидкість матеріальної точки в момент часу t=2c.
2. Відновіть запис. Похідну якої функції потрібно взяти, щоб рівність була правильною?
|
|
|
|
( … )' = - sin x |
( … )' = 2x |
3. Оголошення теми, ціле покладання уроку. Мотивація вивчення теми необхідністю знаходити функцію, похідна якої дорівнює заданій функції. Ознайомлення з очікуваними результатами учнів.
ІІ. Етап навчально - пізнавальної діяльності
- Сприйняття та осмислення матеріалу
- Вч.: Ми нагадали, що а(t)= v'(t) = s''(t) . Нерідко в механіці доводиться розв’язувати обернену задачу: знаходити закон руху за відомим законом зміни швидкості. Приклад з підручника ст. 238 .
Знаходження похідної заданої функції називають диференціюванням. Обернену операцію - знаходження функції за її похідною, називають інтегруванням.
- Означення первісної.
1
-
Розглянемо у=х2+4, у=х2-
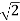 , що мають похідну…(учні відповідаютьу=2х) . Отже ці функції є первісними для функції у=х2. Кожна з функцій у=х2+С , С-довільне число є первісними. Малюнок на дошці (рис 1).
, що мають похідну…(учні відповідаютьу=2х) . Отже ці функції є первісними для функції у=х2. Кожна з функцій у=х2+С , С-довільне число є первісними. Малюнок на дошці (рис 1).
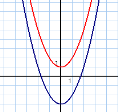 рис.1
рис.1 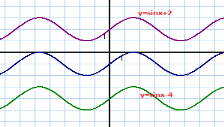 рис. 2
рис. 2
Основна властивість первісної. Ст. 239(**доведення для учнів Д+В рівнів)
- Підведемо підсумки: Якщо функція F є первісною функції f на проміжку , то запис F(х)+С, С-довільне число, називають загальним виглядом первісних функції f на проміжку. Геометрично основна властивість первісної означає, що графіки будь-яких первісних даної функції можна отримати один з одного паралельним перенесенням уздовж осі ординат(рис. 2).
-
Сукупність усіх первісних даної функції у=f(х) називається невизначеним інтегралом і позначається символом
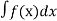 , тобто
, тобто 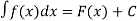 , де F(x)- одна із первісних для функції f(x), а С-довільна стала. В записі f(x)- підінтегральна функція.
, де F(x)- одна із первісних для функції f(x), а С-довільна стала. В записі f(x)- підінтегральна функція.
- Первинне закріплення нового матеріалу
1 ) Установіть, чи функція F є первісною для функції f: №24.1(5,6)
2) Ознайомлення з таблицею первісних. Знаходження первісних та невизначених інтегралів: №24.4
3) Інтерактивна вправа «Навчаючись- навчаємо» ст. 242 Приклад 2. Аналіз прочитаного. Складання алгоритму роботи для виконання подібних вправ. Обговорення.
4) Самостійна робота
|
Серед рівень під керівництвом вчителя №24.8(2) |
Д+В 24.8(3) самостійно. Один учень виконує біля дошки для самоперевірки |
Усний коментар самостійної роботи.
ІІІ. Рефлексія
Інтерактивна вправа «Мікрофон»
- На уроці я дізнався…
- Мені цікаво було з’ясувати…
- Я не вмів… , а тепер умію…
- На наступному уроці я хочу …
ІV. Домашнє завдання.
П24,**доведення теореми,
Серед. №24.2(1,3), Д+В *24.6(1),*24.11(1), вивчити таблицю первісних
2
Урок 2. Тема. Розв’язування вправ (Первісна. Основна властивість первісної. Невизначений інтеграл).
Цілепокладання: закріпити вміння визначати, чи є функція первісною для заданої функції; навичок застосовувати таблицю первісних для знаходження первісних для функцій та обчислювати невизначені інтеграли; знаходити одну з первісних для заданої функції; провести самостійну роботу для визначення рівня засвоєння матеріалу, виявлення помилок, їх корекції.
Формувати вміння аналізувати й узагальнювати інформацію; розвивати увагу, логічне мислення.
Виховувати відповідальність за результат своєї роботи.
Очікуванні результати: учні використовують знання таблиці первісних для знаходження первісних та обчислень невизначених інтегралів ; вміють складати алгоритм до виконання типових вправ; уміють формулювати й висловлювати власну думку, аргументувати її; по результатам самостійної роботи виявляють рівень своїх досягнень з теми.
Обладнання: підручник, малюнки до основної властивості первісної (Використання комп’ютера- слайдів «Графіки первісних» ).
Тип уроку: удосконалення вмінь та навичок.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1) Перевірка ДЗ (Зразки заздалегідь на дошці. Самоперевірка, корекція виконання)
2) Інтерактивна вправа «Мозковий штурм» (запитання-відповідь)
- Поясніть, у якому випадку функція F(х) є первісною функції f(х) на проміжку . Навести приклад.
- Сформулюйте основну властивість первісних. Проілюструйте її на прикладі(геометричний зміст первісних) Використати міні – презентацію «Графіки первісних» (додаток в електронному вигляді).
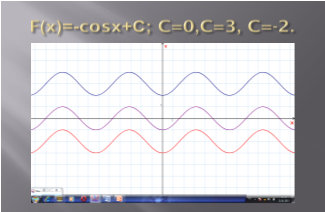
- Дати означення невизначеного інтегралу.
3) Оголошення задач уроку. Виявлення очікуваних результатів.
ІІ. Застосування вмінь та навичок
1) Математичний диктант.
1.Знайдіть всі первісні для функцій: а) f(x)=5; b) f(x)=x5; c)f(x)=![]() ; d) f(x)= 10x:
; d) f(x)= 10x:
e) f(x)=![]() 3
3
Відповіді: a) F(x)= 5x+C; b) F(x)= ![]() +C; c) F(x)= -
+C; c) F(x)= - ![]() +C; d) F(x)=
+C; d) F(x)= ![]() +C; e) F(x)= 2
+C; e) F(x)= 2![]() +C:
+C:
2.Знайдіть інтеграли: a) ![]() ; b)
; b) ![]() ; c)
; c) ![]() ; d)
; d) ![]()
Відповіді: a) 3x+C; b) ![]() +C; c) ex+C; d) sinx+C
+C; c) ex+C; d) sinx+C
2) Інтерактивна вправа «Так чи ні». До заданих на картках рівностей перевірити їх істинність.
![]() ;
; ![]()
2) Колективна робота №24.10(3)
Зразок відповіді до №24.10. Для функції f(х)=![]() знайдіть на проміжку І первісну F:
знайдіть на проміжку І первісну F:
Розв’язання. Для f(х)=![]() , маємо F(x)=ln│х│+С. Для хϵ(-∞;0), то F(x)=ln(-х)+С. Так як F(-е3)=7, то ln e3+C=7, 3ln e+С=7, 3+С=7, С=4. Отже F(x)=ln(-х)+4 для хϵ(-∞;0). Відповідь: F(x)=ln(-х)+4.
, маємо F(x)=ln│х│+С. Для хϵ(-∞;0), то F(x)=ln(-х)+С. Так як F(-е3)=7, то ln e3+C=7, 3ln e+С=7, 3+С=7, С=4. Отже F(x)=ln(-х)+4 для хϵ(-∞;0). Відповідь: F(x)=ln(-х)+4.
3) самостійна робота
|
Серед. рівень під керівництвом вчителя №24.8(1), №24.1(1), №24.4 |
Д+В №24.15**, №24.12*,№24.14* При необхідності надати консультацію |
По можливості контроль виконання учнями самостійної роботи, що надасть можливості їх оцінити.
ІІІ. Рефлексія Інтерактивна вправа «Вибери твердження»
- Все зрозумів, виконав, зможу допомогти іншим.
- Все виконав.
- Можу, але потрібна допомога.
- Нічого не розумію.
- Потрібно, ще тренуватись.
- Такі завдання мені подобаються.
ІV. Домашнє завдання
П24,**доведення теореми,** виведення формули
Серед. №24.9(1,2),№24.5(парні), Д+В *24.11(4),**24.16,*№24.13 Повторити таблицю первісних, ** Підготувати міні презентації « Первісна, невизначений інтеграл».
Зразок відповіді до №24.15**
Доведіть, що функції F1(х)=![]() sin2x і F2(x)= - sin2(x-
sin2x і F2(x)= - sin2(x-![]() ) є первісними функції f(х)= cos2x. При якому значенні С є правильною рівність F1(x)=F2(x)+C?
) є первісними функції f(х)= cos2x. При якому значенні С є правильною рівність F1(x)=F2(x)+C?
Розв’язання.
(F1(х)) ' =![]() sin2x)' =
sin2x)' = ![]() cos2x· (2x)' = cos 2x, отже F1(х)- є первісна функції f(х)= cos2x.
cos2x· (2x)' = cos 2x, отже F1(х)- є первісна функції f(х)= cos2x.
(F2(x)) '=( - sin2(x-![]() ) )' = -2 sin(x-
) )' = -2 sin(x-![]() )· ( sin(x-
)· ( sin(x-![]() ) )'= -2 sin(x-
) )'= -2 sin(x-![]() )· cos(x-
)· cos(x-![]() )· (x-
)· (x-![]() )'=
)'=
4
= -2 sin(x-![]() )· cos(x-
)· cos(x-![]() )= = -sin(2x-
)= = -sin(2x-![]() )· = -(- sin(2x-
)· = -(- sin(2x-![]() ) cos2x, отже F2(х)- є первісна функції f(х)= cos2x.
) cos2x, отже F2(х)- є первісна функції f(х)= cos2x.
Знайдемо значення С для якого є правильною рівність F1(x)=F2(x)+C.
![]() sin2x = - sin2(x-
sin2x = - sin2(x-![]() ) +С ;
) +С ; ![]() sin2x +sin2(x-
sin2x +sin2(x-![]() ) –С =0;
) –С =0; ![]() sin2x +
sin2x + ![]() –С =0 ;
–С =0 ;
![]() sin2x +
sin2x + ![]() –С =0 ;
–С =0 ; ![]() sin2x +
sin2x + ![]() -
- ![]() sin2x - C=0 ; C=
sin2x - C=0 ; C= ![]() .
.
Відповідь: ![]() .
.
Урок 3 Тема. Правила знаходження первісної
Цілепокладання: ознайомити учнів з правилами знаходження первісних, вчити їх застосовувати для знаходження загального вигляду первісних функції та обчисленні невизначеного інтегралу, користуючись знаннями таблиці первісних. Формувати вміння орієнтуватися у видозміненій ситуації, вибирати і використовувати необхідну інформацію для розв’язування задач.
Виховувати наполегливість у досягненні мети.
Очікуванні результати: учні знають правила первісних, доречної їх використовують; вміють висловлювати власну думку, аргументувати її.
Обладнання: підручник, динамічні слайди «Первісні функції», комп’ютерна програма MytestX.
Тип уроку: засвоєння нових знань.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
Епіграф до уроку: Що вмієте того не забувайте, а чого не вмієте, того навчайтесь. В.Мономах.
1) Інтерактивна вправа. Бліц- опитування:
- Яку загальну тему вивчаємо;
- Яку функцію називаємо первісною для даної функції f(x)?
- Записати всі формули знаходження первісних, з використанням невизначеного інтегралу (учні виконують на окремих листах, один учень- на скритій дошці для самоперевірки)
- Що називається невизначеним інтегралом?
- Презентація творчих робіт (зразки подані в електронному вигляді)
5


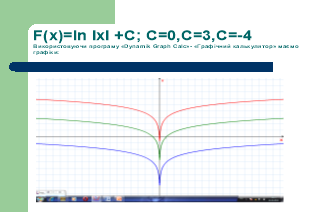
- Вказати алгоритм знаходження однієї з первісних, яка проходить через дану точку.
2) Електронний тест «Формули первісних» (комп’ютерна програма MytestX).
3) Оголошення теми, ціле покладань уроку. Ознайомлення учнів з очікуваними результатами.
ІІ. Етап навчально- пізнавальної діяльності
- Пояснення вчителя з елементами бесіди
Вч.: Є три правила знаходження первісних: ( Підручник А.Г.Мерзляк 11 клас. Алгебра . Профільний рівень ст. 245)
Теорема : Якщо функції F і G є відповідно первісними функцій f і g на проміжку І, то на цьому проміжку функція у= F(x)+G(x) є первісною функції y=f(x)+g(x).
Доведення: Якщо F(x) - первісна для функції f(x), то F’(x)=f(x). Аналогічно, якщо G(x) – первісна для g(x) , то G’(x)=g(x) . Тоді за правилом диференціювання маємо:
(F(x) + G(x) )’ = F’(x) + G’(x) = f(x) +g(x), а це означає , що F(x) +G(x) - первісна для f(x)+g(x).
Запис: ![]()
![]() +
+ ![]() F(x)+G(x)+C (Інтеграл для суми дорівнює сумі інтегралів для доданків).
F(x)+G(x)+C (Інтеграл для суми дорівнює сумі інтегралів для доданків).
Зауваження: Правило поширюється на будь яку кількість доданків.
Розгляд прикладу 1 на ст. 247.
Теорема: Якщо функція F є первісною функції f на проміжку І та k - деяке число, то на цьому проміжку функція у=kF(x) є первісною функції y=kf(x).
6
Доведення: Якщо F(x) - первісна для функції f(x), то F’(x)=f(x). Враховуючи, що сталий множник можна виносити за знак похідної, маємо ( kF(x) )’= k(F(x))’= kf(x) ,а це означає , що F(x) - первісна для f(x).
Запис: ![]() k
k ![]() = kF(x) +C (Сталий множник можна виносити за знак інтеграла).
= kF(x) +C (Сталий множник можна виносити за знак інтеграла).
Теорема: Якщо функція F є первісною функції f на проміжку І та k - деяке число, відмінне від нуля, то на цьому проміжку функція у=![]() F(kx+b) є первісною функції y=f(kx+b).
F(kx+b) є первісною функції y=f(kx+b).
Доведення: Якщо F(x) - первісна для функції f(x), то F’(x)=f(x). Враховуючи правило обчислення похідної складеної функції, маємо ( ![]() F(kx+b))’=
F(kx+b))’= ![]() F’(kx+b) (kx+b)’ =
F’(kx+b) (kx+b)’ = ![]() f(kx+b)· k= f(kx+b)
f(kx+b)· k= f(kx+b)
Запис: ![]() F(kx+b)+C
F(kx+b)+C
Розгляд прикладу 2 ст 247.
- Первинне закріплення нового матеріалу
1.Розв. вправ біля дошки з коментуванням правил: №25.1(непарні), №25.3 *(4,7)
2.Обговорення прикладу 3 ( Підручник ст.248 ).
3.Розв’язування вправ
|
Серед рівень з вчителем №25.6(2,3) |
Д+В самостійно №25.6(*4,*6),два учні виконують на скритій дошці для самоперевірки та обговорення) |
4.Проблемне запитання . Ознайомившись з матеріалом пункту, чи виникає у вас запитання, як знайти первісні функцій y=f(x)g(x)? y=![]() ? y= f(g(x)), якщо відомі первісні функцій y=f(x), y=g(x).
? y= f(g(x)), якщо відомі первісні функцій y=f(x), y=g(x).
(Вч. На жаль, загальних правил знаходження первісних таких функцій не існує.
Розгляд прикладу.
5.Колективно **№25.15(1) . Нагадування формул до кожного завдання (10 клас «Тригонометрія»)
Зразок розв’язання:** ![]()
![]() dx=
dx=![]()
![]() =
=
= ![]() (x -
(x -![]() sin(2x))+C=
sin(2x))+C= ![]() x -
x - ![]() sin2x+C. Відповідь:
sin2x+C. Відповідь:![]() x -
x - ![]() sin2x+C.
sin2x+C.
ІІІ.Рефлексія
Інтерактивна вправа «Закінчити речення»
- Сьогодні на уроці я навчився…
- Було цікаво…
- Було важко…
- Мої відчуття, щодо засвоєння матеріалу…
ІV. Домашнє завдання
П24,25**доведення теорем, №25.1(2,8,10)№25.3(*8), №25.6(*5,*8), **№25.15(3)
7
Урок 4 Тема : Розв’язування вправ.
Цілепокладання: відпрацювати навички застосування правил знаходження первісних; застосування первісної в фізиці; розвивати навички розв’язувати різнорівневі вправи, здійснювати самооцінку своїх навчальних досягнень.
Розвивати вміння узагальнювати та робити висновки.
Виховувати відповідальність, самостійність.
Очікувані результати: учні використовують таблицю первісних та правила інтегрування, знаходять первісні у різнорівневих задач,знаходять та виправляють помилки.
Обладнання: підручник, лист самооцінки, набір «Кольоровий тест», збірник Є.П.Нелін, О.М.Роганін «Зошит для поточного і тематичного оцінювання. Профільний рівень. 11 клас». «Гімназія» ,2011.
Тип уроку: удосконалення вмінь та навичок. Урок- практикум
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1) Перевірка ДЗ (Зразки заздалегідь на дошці. Самоперевірка, корекція виконання)
2) Оголошення теми, плану роботи. Виявлення в учнів очікуваних результатів
Епіграф до уроку: Досягнути успіху можна тільки тоді, коли є певна мета.
Знайомство з листом самооцінки та планом роботи на уроці:
Дата_________________,П.І.________________________
|
Теоретичні знання Правильна Відповідь 1б, іІндив.робо та 2б |
Самодиктант правильні три відповіді-1б, 1-2 помилки-0,5б |
Кольоровий тест не помилився-1б, були помилки-0,5б |
Розв.вправ з вчителем -1б, Індив. робота 2б |
СР 1-4 завдання-2б, 5,6 завдання по 1б |
Додаткові вправи, активна участь на уроці- 1б |
Загальна к-ть балів |
|
|
|
|
|
|
|
|
ІІ. Актуалізація опорних знань
1)Перевірка теоретичних знань
|
Для класу вправа «Запитання-відовідь»
|
Один учень готує на дошці записи до введення поняття первісної та невизначеного інтегралу |
Один учень готує записи до відповіді на запитання по правилам знаходження первісної, **одне з доведенням |
2) Самодиктант (Завдання на окремі картки.)
Запишіть за допомогою невизначеного інтегралу:
- (-sinx+C)’= -cosx; 2. (-cos2x+C)’= sin2x; 3. ( ln sinx+C)’= ctgx
Самоперевірка за зразками на дошці.
8
3)Інтерактивна вправа «Кольоровий тест» (Варіанти відповідей заздалегідь на дошку)
Серед наведених нижче функцій, укажіть ту, первісною для якої є функція F(x)=-sinx+C.
(Учні по команді піднімають колір картки з відповідною тестовою буквою a); b); c); d))
а ) f(x)=cosx; в) f(x)= -cosx; c) f(x)=x д) f(x)= - sinx
Серед наведених нижче функцій, укажіть ту, первісною для якої є функція F(x)= ctgx+C.
а) f(x)=![]() ; b) f(x)= -
; b) f(x)= - ![]() ; c) f(x)=
; c) f(x)= ![]() ; d) f(x)= -
; d) f(x)= - ![]() .
.
Серед наведених нижче функцій, укажіть ту, первісною для якої є функція F(x)=![]() +C.
+C.
а) f(x)=4 · ![]() ; b) f(x) = 24x6; c) f(x)= -x – 4; d) f(x)= 20x6
; b) f(x) = 24x6; c) f(x)= -x – 4; d) f(x)= 20x6
ІІІ Удосконалення вмінь та навичок.
1)Розв’язування вправ
|
Колективно №25.5(8) |
Індивідуально учень біля дошки №25.5(*10). Призначити сильнішого учня консультантом |
Індивідуально учень біля дошки №25.6(*8). Призначити сильнішого учня консультантом |
Швидка перевірка та при необхідності обговорення робіт.
2)Колективне обговорення та розв’язання з коментуванням на місці №25.11
Задача . Розв’язання v(x)= 6t2+1(м/с), t=3c, S=10м.
Визначимо координату s(t), знаючи закон зміни швидкості. Знаємо, що s’(t)= v(t), отже функція s(t)- є первісною для функції v(t)
![]() =6·
=6· ![]() +t +C = 2t3+t+C; s=10; t=3, то 54+3+C=10; C= - 47.
+t +C = 2t3+t+C; s=10; t=3, то 54+3+C=10; C= - 47.
Отже s(t)= 2t3+t-47 (м).
Відповідь: s(t)= 2t3+t-47 м.
3)Обговорення та розв’язання вправи високого рівня №25.17**
Задача. Для функції f(x)= 2х2+3х знайдіть таку первісну, що пряма у= 5х-2 є дотичною до її графіка .
Розв’язання. f(x)= 2х2+3х. F(x)- первісна функції f(x). F(x)= ![]() +
+ ![]() +C. Так як пряма у= 5х-2 є дотичною до одного із графіків первісних, то k= f’(x0)=5, враховуючи F’(x)=f(x), маємо 2х 02+3х 0 =5, 2х 02+3х 0 -5=0, D=49, х 0=1 або х 0= -2,5. Точка (х0;у0)- спільна точка графіків дотичної у= 5х-2 та графіка однієї із первісних : у0=5·1-2=3, у0=5·(-2,5)-2=-12,5-2=-14,5.Знайдемо значення С:
+C. Так як пряма у= 5х-2 є дотичною до одного із графіків первісних, то k= f’(x0)=5, враховуючи F’(x)=f(x), маємо 2х 02+3х 0 =5, 2х 02+3х 0 -5=0, D=49, х 0=1 або х 0= -2,5. Точка (х0;у0)- спільна точка графіків дотичної у= 5х-2 та графіка однієї із первісних : у0=5·1-2=3, у0=5·(-2,5)-2=-12,5-2=-14,5.Знайдемо значення С: ![]() +
+ ![]() +С=3, С=
+С=3, С=![]() ;
;
![]() · ( -
· ( - ![]() ) +
) + ![]() +С =-14
+С =-14![]() , С=-
, С=- ![]() = -13
= -13![]() . Маємо дві первісних, для яких пряма у= 5х-2 є дотичною : F(x)=
. Маємо дві первісних, для яких пряма у= 5х-2 є дотичною : F(x)= ![]() +
+ ![]() +
+![]() ; F(x)=
; F(x)= ![]() +
+ ![]() -13
-13![]() .
.
Відповідь: F(x)= ![]() +
+ ![]() +
+![]() ; F(x)=
; F(x)= ![]() +
+ ![]() -13
-13![]() .
.
4)Самостійна робота Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень 11 клас ст.57. Варіант1 або варіант 2.
Вчителю слід контролювати вчасне заповнення листа самооцінки.
9
IV.Рефлексія Бесіда.
- Чи здійснились наші очікування .
- Чи задоволені ви результатами сам. роботи.
Результати роботи на уроці визначимо «Райтингом» (це дріб, перша оцінка- оцінка учня,а в знаменнику оцінка вчителя, яку діти дізнаються на наступному уроці після перевірки зошитів)
V. Домашнє завдання
П24,25,**доведення теорем,**вивід формули, №24.10(2), *25.5(4,6), **№25.16, ** №25.18
Урок 5 Тема. Розв’язування вправ. Самостійна робота.
Цілепокладання: перевірити рівень засвоєння знань вивчених питань даної теми; провести корекцію знань учнів.
Розвивати вміння правильно висловлювати свої думки в письмовому вигляді.
Виховувати дисциплінованість, самостійність, відповідальність.
Очікувані результати: швидко усно обчислюють, вміють користуватись комп’ютерною програмою MytestX, вміло встановлюють відповідність, правильно ведуть математичні письмові записи, обґрунтовують виконання,знаходять та виправляють помилки.
Обладнання: підручник, комп’ютерна програма MytestX, збірник Є.П.Нелін, О.М.Роганін «Зошит для поточного і тематичного оцінювання. Профільний рівень. 11 клас». «Гімназія», 2011
Тип уроку: урок контролю і корекції знань, умінь і навичок.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1) Перевірка ДЗ
Запитання до виконаної домашньої роботи.
2)Оголошення результатів «Райтингу» попереднього уроку.
3) Оголошення теми, ціле покладань уроку. Виявлення в учнів очікуваних результатів
ІІ. Актуалізація опорних знань
1)Усний рахунок .
Електронний тест «Невизначений інтеграл» .(Максимальна оцінка 10 балів за правильні відповіді до 12 запитань тесту протягом 5 хв.)
- Встановити відповідність між інтегралом та його значенням. Письмова робота.
|
|
А) F(x)=eˣ -2sinx +C |
|
|
Б) F(x)= 4ln│x│+ |
|
|
B) F(x)= |
|
4) |
Г) F(x)=eˣ +2sinx +C
|
|
|
Д) F(x)= 3ln│x│- |
Відповідь: 1-д, 2-а, 3-б, 4- в.
10
ІІІ. Перевірка знань, умінь і навичок
Самостійна робота.
- Виконання завдань: Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень 11 клас, ст.59. Варіант1 або варіант 2.
Вчитель має роль консультанта, при необхідності надає допомогу.
- Корекція знань. Відпрацювання помилок або додаткова індивідуальна різнорівнева вправа.
№25.4, №**25.15(2), *№25.10
Результати оцінювання учні отримують після перевірки зошитів.
ІІІ.Рефлексія
Інтерактивна вправа « Рефлексійні картки»
Оцініть свою роботу і підніміть рефлексивні картки :
- синій- працював добре, своєю роботою задоволений;
- зелений- виникли деякі труднощі;
- жовтий- було складно, потрібна допомога вчителя.
ІV. Домашнє завдання
П24,25 ,знання формул,№25.2(4,8,)№25.4(*7), №*25.7, **№25.15(3)
Зразок розв’язання до №*25.7
Задача . Для функції f(x)=4х3+4х знайдіть первісну F, один з нулів якої дорівнює -1. Знайдіть решту нулів цієї первісної.
Розв’язання. Функції f(x)=4х3+4х, F(x)- її первісна. F(x)=![]() +
+![]() +C= x4 + 2x2 +C. Використаємо,що один із нулів первісної дорівнює -1. x4 + 2x2 +C=0,х=-1, то С=-3. Отже первісна має вигляд F(x) = x4 + 2x2 -3. Знайдемо інші нулі первісної: x4 + 2x2 -3=0, нехай х2=а, то а2+2а-3=0, а=-3 або а=1. Маємо х2=-3 , розв’язку немає, х2=1, х=-1 або х= 1.
+C= x4 + 2x2 +C. Використаємо,що один із нулів первісної дорівнює -1. x4 + 2x2 +C=0,х=-1, то С=-3. Отже первісна має вигляд F(x) = x4 + 2x2 -3. Знайдемо інші нулі первісної: x4 + 2x2 -3=0, нехай х2=а, то а2+2а-3=0, а=-3 або а=1. Маємо х2=-3 , розв’язку немає, х2=1, х=-1 або х= 1.
Відповідь: F(x) = x4 + 2x2 -3, х=1.
Урок 6 Тема. Розв’язування вправ
Урок- практикум.
Цілепокладання: відпрацювати навички застосовувати правила знаходження первісних; вчити розв’язувати різнорівневі вправи, застосувати ІКТ для повторення геометричного змісту невизначеного інтегралу.
Активізувати пізнавальну діяльність, сприяти розвитку логічного мислення, уваги учнів. Виховувати інтерес до вивчення предмету, відповідальність за результати власної та колективної роботи.
Очікувані результати: швидко усно та письмово обчислюють невизначені інтеграли, вміють користуватись комп’ютерною програмою «Dynamik Graph Calc v.1.0.7», уміють формулювати й висловлювати власну думку, аргументувати її під час роботи в групі, обґрунтовують виконання задач, знаходять та виправляють помилки.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1) Перевірка ДЗ (Зразки заздалегідь на дошці. Самоперевірка, корекція виконання)
11
2) Оголошення теми, цілепокладань уроку. Виявлення в учнів очікуваних результатів
ІІ. Застосування вмінь та навичок
- Усний рахунок. Знайдіть первісні для функцій:
|
|
|
|
|
|
|
|
|
|
11)Sin( |
12)x |
Вчитель показує картку, учні відповідають.
- Відпрацювання вмінь учнів знаходити первісні для функцій:
(завдання за Збірником «Первісна та інтеграл» - Газета «Математика в школах України» №31(295) листопад 2010р.)
Вчитель та учні високого рівня виконують роль при необхідності консультантів. Правильні розв’язання позначають знаком «+», до неправильно виконаних вправ учні повертаються знову.
- Робота в групах.
Застосування ІКТ для повторення геометричного змісту невизначеного інтегралу.
1. Клас поділити по 3 чоловіки(кожна група має комп’ютер). Розподілити обов’язки;секретар ( контролює виконання роботи по обчисленню первісної), лідер
( переносить результат в спільну презентацію), редактор ( виконує графічний малюнок).
2. Завдання учням: Для заданих функцій знайти первісні, за допомогою програми «Dynamik Graph Calc v.1.0.7» виконати малюнки первісних.
3. План роботи за комп’ютером: відкрити програму, встановити «Графічний калькулятор» побудувати два- три графіка функцій первісних , нажати одночасно кнопки Ctrl+PrtSc Sys Rg, відкрити програму Paint , вставити, обрізати, виділити все, зберегти в документі Word, перенести матеріал в загально створену презентацію робіт.
Завдання: 1 група у=2х, 2 група у=2cos2x, 3 група у=![]() , 4 група у=ln 5·5x ,
, 4 група у=ln 5·5x ,
5 група у=![]() .
.
Результати обчислення первісних: : 1 група F(x)=х2+С, 2 група F(x)=sinx+C,
3 група F(x)=tgx +C 4 група F(x)=5x+C , 5 група F(x)=![]() +C.
+C.
Зразок учнівської роботи 1групи:
12
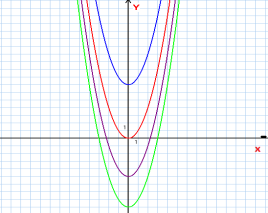
Перегляд презентацій з обговоренням.
ІІІ.Рефлексія
Закінчіть відповідний вислів. Своєю роботою на уроці я…
|
задоволений, тому що… |
Не зовсім задоволений тому що… |
Не задоволений, тому що… |
Визнач на якому рівні засвоєна тема «Первісна та невизначений інтеграл»
ІV. Домашнє завдання
П24,25 ,знання формул, №24.11(4), №25.2(1,5))№25.5(*5),*№25.8
Урок 7 Тема . Геометричний зміст та означення визначеного інтегралу. Формула Ньютона-Лейбніца.
Цілепокладання: познайомити дітей з криволінійними трапеціями, дати означення визначеного інтегралу, вчити застосовувати формулу Ньютона-Лейбніца для обчислення визначених інтегралів.
Формувати вміння грамотно формулювати власні думки, сприяти розвитку логічного мислення, пам’яті, уваги учнів.
Виховувати працьовитість, спостережливість, творчу активність
Очікуванні результати: учні усвідомлюють основні поняття теми, доцільно використовують, добирають графіки для знаходження визначеного інтегралу, учні обґрунтовують виконання вправ щодо обчислень визначених інтегралів, супроводять відповідь докладною розповіддю.
Обладнання до уроку: динамічні слайди презентації «Інтеграл та його застосування».
Структура, основний зміст, методи діяльності:
І.Мотиваційно- організаційний етап
Епіграфом до уроку дібрано слова видатної жінки- математика С. Ковалевської : «Серед усіх наук, що відкривають шлях до пізнання законів природи, найвеличнішою є математика».
У попередніх класах ви навчились обчислювати площі прямокутника, трикутника, паралелограма, трапеції, круга, його частин (Можна супроводити картками формул
13
площ). У математиці розроблені методи, що дозволяють обчислювати площі фігур, обмежених кривими лініями. Використовуючи знання про первісну, ми навчимося знаходити площі фігур, які називаються криволінійними трапеціями.
Використання слайдів Презентації «Інтеграл та його застосування»
ІІ. Етап навчально - пізнавальної діяльності
- Пояснення вчителя з елементами бесіди
- Означення фігури: Фігуру, обмежену графіком функції f і прямими у=0, х=а і х=в, називають криволінійною трапецією.
Робота з підручником ст. 254. Малюнки криволінійних трапецій. В підручнику та на слайдах(слайд 15).
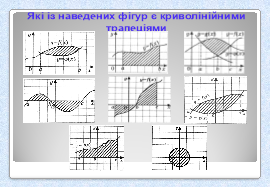
- Теорема . Площа S криволінійної трапеції, обмеженої графіком функції у= f(х) і прямими у=0, х=а і х=в(а˂в), можна обчислити за формулою S= F(b)-F(a),де F- будь-яка первісна функції f на відрізку [а;в ]
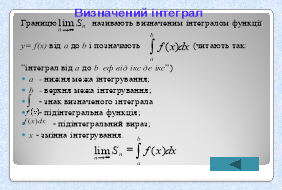
Доведення вчителем. (Використати Підручник ст. 155-156). Супровід пояснення слайдами 16,17,18.


14
У площині ХОУ розглянемо фігуру АВСД, обмежену прямими х=а, у=b, віссю ОХ і графіком функції f, неперервної та невід’ємної на відрізку [а;b]. Цю фігуру називають криволінійною трапецією. Обчислимо її площу. Для цього поділимо відрізок [а;b] на r рівних частин точками а= х0< х1 <… < хv-1 < хv <… < xr-1 < xr =b. У результаті дістанемо r рівних відрізків [хv-1; xv], v=1,2,…, r, довжина яких дорівнює ![]() На кожному з відрізків [хv-1; xv], як на основі побудуємо прямокутник з висотою f(xᵥ₋₁), що дорівнює значенню функції f у лівому кінці відрізка. Площа кожного такого прямокутника становитиме
На кожному з відрізків [хv-1; xv], як на основі побудуємо прямокутник з висотою f(xᵥ₋₁), що дорівнює значенню функції f у лівому кінці відрізка. Площа кожного такого прямокутника становитиме ![]() , а площу фігури, утвореної з побудованих прямокутників, можна визначити за формулою:
, а площу фігури, утвореної з побудованих прямокутників, можна визначити за формулою:
![]()
![]() . Суми такого вигляду називають інтегральними . Одержана сума наближено визначає площу заданої криволінійної трапеції АВСД. Границю інтегральної суми Sr , коли n→∞ називають визначеним інтегралом функції f на відрізку [а;b] і позначають
. Суми такого вигляду називають інтегральними . Одержана сума наближено визначає площу заданої криволінійної трапеції АВСД. Границю інтегральної суми Sr , коли n→∞ називають визначеним інтегралом функції f на відрізку [а;b] і позначають ![]() Числа а і b називають відповідно нижньою та верхньою межами інтегрування, f(x) – підінтегральним виразом,
Числа а і b називають відповідно нижньою та верхньою межами інтегрування, f(x) – підінтегральним виразом, ![]() - знаком інтеграла, х – змінною інтегрування. Отже за означенням матимемо:
- знаком інтеграла, х – змінною інтегрування. Отже за означенням матимемо: ![]() . Функцію f, для якої існує інтеграл, називають інтегрованою на відрізку[а;b]. Зокрема, інтегрованою на відрізку [а;b] є будь- яка функція, неперервна на цьому відрізку. Із задачі про площу криволінійної трапеції випливає, що
. Функцію f, для якої існує інтеграл, називають інтегрованою на відрізку[а;b]. Зокрема, інтегрованою на відрізку [а;b] є будь- яка функція, неперервна на цьому відрізку. Із задачі про площу криволінійної трапеції випливає, що ![]()
- Означення визначеного інтегралу . Підручник ст. 257. Введення формули. Слайд 19

ІІІ. Первинне закріплення нового матеріалу.
- Інтерактивна вправа «Прокоментувати!» стр 259 Підручник. Приклад 3.
15
2) Розв’язування вправ колективно на відпрацювання навиків знаходити визначений інтеграл.
Обчисліть: 1. ![]()
![]()
![]()
![]()
Відповідь: ![]()
3)Знайти площу криволінійної трапеції
- Колективно № 26.1. (г,є) .
- Самостійно №26.1.(б,д). Два учні біля дошки для самоперевірки та обговорення.
4)Обчисліть визначений інтеграл: Колективно №26.8 *(3,7,8)
5)Самостійна робота
|
Учні середнього рівня під контролем вчителя виконують №26.3(непарні) |
Самостійно №26.8.(*5,*9,). Два учні біля дошки для самоперевірки та обговорення
|
Самостійно №26.8.(**12). Учень біля дошки для самоперевірки та обговорення
|
Учні ,які працювали самостійно, отримають додаткові питання та оцінюються.
6)Обчисліть визначений інтеграл: **№26.19(1) Колективне обговорювання. Нагадування формул «Тригонометрія 10 клас». Зразок розв’язання:
![]() =
=![]() =
= ![]() tg3x-x) |
tg3x-x) |![]() =
= ![]() tg
tg![]() -
-![]() =
= ![]() -
-![]() =
=![]()
Відповідь: ![]() .
.
ІІІ. Рефлексія Інтерактивна вправа «Мікрофон»
- Я дізнався…
- Я навчився…
- Я зрозумів…
- Я вмію…
- Мене здивувало…
- Я збагатився інформацією про…
- Мене зацікавило…
- Я ніколи не чув про…
ІV. Домашнє завдання
П26**доведення теореми,** вивід формули
№26.3 (4,6,8),№26.1(в),*26.8(2,4,11), **№26.19( 2,3)
** Підготувати історичну довідку (використати матеріал підручника ст. 274 «Коли зроблені уроки» використати інформацію «Розумом він перевершив рід людський»)
16
Урок 8 . Тема. Розв’язування вправ.
Цілепокладання: розвивати навички знаходити площі найпростіших криволінійних трапецій, вмінь обчислювати визначені інтеграли.
Формувати вміння міркувати за аналогією; розвивати увагу,логічне мислення, пам’ять.
Виховувати працьовитість, уважність, спостережливість, об’єктивність та чесність під час оцінювання власних знань.
Очікувані результати: учні доцільно використовують таблицю первісних та правила інтегрування , застосовують формулу Ньютона-Лейбніца, знаходять визначені інтеграли у різних типах задач, на різних рівнях. Знаючи, що визначений інтеграл використовують для визначення площ криволінійних трапецій , обчислюють їх площі.
Обладнання до уроку: динамічні слайди презентації «Графіки первісних» , «Інтеграл та його застосування», лист самооцінки знань, кросворд.
Тип уроку: удосконалення вмінь та навичок.
Структура, основний зміст, методи діяльності:
І. Мотиваційно - організаційний етап
1) Перевірка ДЗ (Зразки заздалегідь на дошці. Самоперевірка, корекція виконання)
2) Оголошення теми, цілепокладань уроку. Виявлення в учнів очікуваних результатів.
Знайомство з листом самооцінки та планом роботи на уроці:
Дата_________________,П.І.________________________
|
1. «Історія виникнення інтегралу» - участь 1бал |
2. «Огляд знань»: Відповідь на запитання 1 бал |
Правильний ключ - 2 бали |
|
4.Різнорівнева робота Середній рівень-2б Достатній рівень-3б Високий рівень -3б |
5. «Я вірю в свої сили» -за кожну вправу по 1 балу |
Загальна кількість балів:
|
ІІ. Застосування вмінь та навичок.
- Екскурсія в минуле «Історія виникнення інтегралу» Розповіді учнів. Використання презентації - фото-колаж «Історія інтегралу».
Якими мудрими Ньютон із Лейбніцем були,
Якими барвами їх формули заграли,
Яку могутність побачили, коли
Зійшлись їх похідні та інтеграли!
Зійшлись - немов злилися два струмки
В стократ потужнішу ріку єдину.
Їх теоремі давній завдяки те,
Що колись долали вчені за віки,
Тепер школяр долає за годину.
- Інтерактивна вправа «Огляд знань»:
- Поясніть, у якому випадку функція F(х) є первісною функції f(х) на проміжку . Навести приклад.
17
2.Сформулюйте основну властивість первісних. Проілюструйте її на прикладі (геометричний зміст первісних). Використати міні – презентацію «Графіки первісних» (додаток в електронному вигляді).
3. Дати означення невизначеного інтегралу.
4. Записати всі формули знаходження первісних, з використанням невизначеного інтегралу.
5. Дати означення визначеного інтегралу, знання формули Ньютона-Лейбніца для обчислення визначених інтегралів.
6.** Доведення теореми . Площа S криволінійної трапеції, обмеженої графіком функції у= f(х) і прямими у=0, х=а і х=в(а˂в), можна обчислити за формулою S= F(b)-F(a),де F- будь-яка первісна функції f на відрізку [а;в ]
- Інтерактивна вправа «Знайди помилку» (завдання – виписати вправу в якій на думку учня допущено помилку, запис в зошиті зробити з правильним результатом)
|
1. =ctgx+C |
2.
= |
3. |
4. |
|
5.
= |
6. =ln(x+3)+C |
7. |
8.
= 3eˣ - |
Ключ (Помилки у вправах ) 3,5,6,8
- Робота за готовим малюнком. Підручник ст. 263 №26.2(в,г)
- Різнорівнева робота
|
Учні середнього рівня виконують № 26.4 (непарні) Три учні виконують на скритій дошці для обговорення |
Учні достатнього рівня виконують№26.8*(6,7,10) Три учні виконують на дошці для обговорення |
Учні високого рівня займаються самоосвітою Використати матеріал надрукований в підручнику Є.П.Неліна , О.Є. Долгової «Алгебра і початки аналізу» 11 клас. Харків 2008, ст199,204-205 «Означення визначеного інтегралу через інтегральні суми» Використати «Тихе опитування» для перевірки усвідомлення матеріалу. |
Обговорити виконані вправи. Здійснити корекцію.
- Інтерактивна вправа «Я вірю в свої сили». Обчисліть інтеграли:
![]()
![]() *у=
*у=![]() **y=
**y=![]() **y=
**y=![]()
18
Учні, які не знають, як виконувати запропонувати посильні завдання зі збірника «Первісна та інтеграл» »- Газета «Математика в школах України» №31(295) листопад 2010р.)
- Інтерактивна вправа «Релейна КР» на 10хв. Хто більше виконає вправ №26.8.(Попередньо в учнів забрати робочі зошити, перевірити роботи на попередніх етапах уроку). По закінченні перевірити декілька робіт, оцінити.
ІІІ.Рефлексія Кросворд:
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
і |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. Першу букву якого слова нагадує знак інтеграла? |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2.Хто з відомих математиків - фізиків дослідив фізичний зміст інтеграла? |
|
|
||||||||||||||||||||
|
3. Хто з відомих математиків дослідив геометричний зміст інтеграла? |
|
|
|
|
||||||||||||||||||
|
4. Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла? |
||||||||||||||||||||||
|
5. Як називається функція, яка стоїть під знаком інтеграла? |
|
|
|
|
|
|
|
|||||||||||||||
|
6. Як називається множник dx у підінтегральному виразі? |
|
|
|
|
|
|
|
|
||||||||||||||
|
7. Як називається операція, обернена до операції диференціювання? |
|
|
|
|
||||||||||||||||||
Відповіді:
- Першу букву якого слова нагадує знак інтеграла? ( Summa - сума)
- Хто з відомих математиків - фізиків дослідив фізичний зміст інтеграла? (Ньютон)
- Хто з відомих математиків дослідив геометричний зміст інтеграла? (Лейбніц)
- Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла?(Криволінійна)
- Як називається функція, яка стоїть під знаком інтеграла? (підінтегральна)
- Як називається множник dx у підінтегральному виразі? (Диференціал)
- Як називається операція, обернена до операції диференціювання? (Інтегрування)
ІV. Домашнє завдання
П26**доведення теореми,** виведення формули 19
№26.4(парні), *№26.9(1,9), **26.20(3). Підготовка до підсумкового уроку за інформаційною карткою для кожного учня:
1. Поясніть, у якому випадку функція F(х) є первісною функції f(х) на проміжку . Навести приклад.
2.Сформулюйте основну властивість первісних. Проілюструйте її на прикладі(геометричний зміст первісних) Використати міні – презентацію «Графіки первісних» (додаток в електронному вигляді).
3. Дати означення невизначеного інтегралу.
4. Записати всі формули знаходження первісних, з використанням невизначеного інтегралу
5. Дати означення визначеного інтегралу, знання формули Ньютона-Лейбніца для обчислення визначених інтегралів.
6.** Доведення теореми . Площа S криволінійної трапеції, обмеженої графіком функції у= f(х) і прямими у=0, х=а і х=в(а˂в), можна обчислити за формулою S= F(b)-F(a),де F- будь-яка первісна функції f на відрізку [а;в ]
7.** Означення визначеного інтегралу через інтегральні суми.
Урок 9 Тема. Роз’язування вправ «Первісна та інтеграл»
Цілепокладання: перевірити рівень знань і умінь учнів обчислювати визначені інтеграли.
Формувати вміння аналізувати інформацію, розвивати увагу, логічне мислення, пам’ять.
Виховувати відповідальність за результати своєї роботи.
Очікувані результати: застосовують формулу Ньютона-Лейбніца, знаходять визначені інтеграли у різних типах задач, на різних рівнях; знаходять та виправляють помилки.
Обладнання: картка - текст діагностичної контрольної роботи, підручник.
Тип уроку: контроль і корекція знань, умінь та навичок.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
Девіз уроку: До знань ведуть три шляхи:
Шлях наслідувань - він найлегший;
Шлях міркувань - цей шлях благородний;
Шлях досвіду – найважчий. Конфуцій.
1) Перевірка ДЗ (Зразки заздалегідь на дошці. Самоперевірка, корекція виконання. Завдання високого рівня коментує один із учнів)
2) Оголошення теми, цілепокладань уроку. Виявлення в учнів очікуваних результатів.
Вчитель налаштовує учнів на роботу, роздає на кожну парту текст діагностичної контрольної роботи.
ІІ. Перевірка знань і вмінь учнів
Для зручності контролю виконання робіт та швидкої перевірки вчитель має розв’язки:
Завдання рівня А (6 балів)
20
-
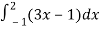 = ... 1
= ... 1 
-
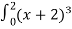 dx= … 60
dx= … 60
-
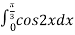 = …
= … 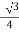
-
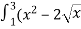 )dx= … 10-4
)dx= … 10-4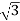
-
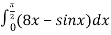 = … π²-1
= … π²-1
-
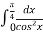 = … 1
= … 1
Завдання рівня Б (оцінка 9балів)
-
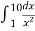 = … 0,9
= … 0,9
-
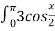 dx= … 6
dx= … 6
-
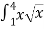 dx= … 12,4
dx= … 12,4
-
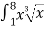 dx= … 54
dx= … 54
-
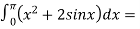 ….
….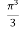 +4
+4
-
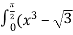 cosx)dx= …
cosx)dx= … 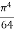 -
-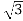
-
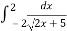 = …. 4
= …. 4
-
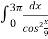 = … 9
= … 9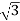
Завдання рівня В (оцінка 12 балів)
15,16,17 Доведіть справедливість рівностей
-
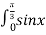 dx=
dx=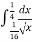
-
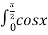 dx=
dx=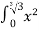 dx
dx
-
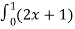 dx=
dx= 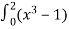 dx
dx
Обчисліть інтеграли
-
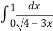 = …
= …
-
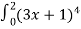 dx= … 1120,4
dx= … 1120,4
-
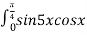 dx= …
dx= … 
-
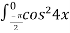 dx= …
dx= … 
В кожному рівні слід виконати 6 завдань. Інші вправи є додаткові.
ІІІ.Етап корекції (за 15 хвилин до кінця уроку)
Вчитель виявляє у дітей, які вправи не вдалося виконати. Учні коментують і пояснюють ці вправи в робочих зошитах (попередньо зібрати листи сам.роботи).
ІV. Рефлексія.
Результати роботи на уроці визначимо «Райтингом» (це дріб, перша оцінка- оцінка учня,а в знаменнику оцінка вчителя, яку діти отримають на наступному уроці після перевірки зошитів, листів СР).
21
V. Домашня робота
Повторити формули, визначення П24,П25.
Тест «Перевір себе» підручник ст. 276, 1-5,7завдання тести,* 6,*8-**12 з поясненнями.
Урок 10 Тема. Роз’язування вправ «Первісна та інтеграл»
Цілепокладання: узагальнити та систематизувати знання з вивченої теми, підготовка до КР. Перевірити рівень засвоєння знань з теми «Первісна. Інтеграл» шляхом проведення самостійної роботи. Розвивати математичні здібності учнів, формувати навички самоконтролю. Виховувати старанність, самокритичність, почуття відповідальності, свідоме ставлення до навчання.
Очікувані результати: застосовують формулу Ньютона-Лейбніца, знаходять визначені інтеграли у різних типах задач, на різних рівнях; уміють формулювати й висловлювати власні думки; знаходять та виправляють помилки.
Обладнання: лист самооцінки, міні – презентацію «Графіки первісних», Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень ,11 клас.
Тип уроку: систематизація і узагальнення знань.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1) Перевірка наявності ДР . Обговорення проблем, які виникли . 10,11,**12 завдання подати заздалегідь на дошку.
Зразок виконання завдання **12 . Обчисліть інтеграл ![]() )dx, якщо інтеграл
)dx, якщо інтеграл ![]() dx =2. Розв’язання
dx =2. Розв’язання ![]() )dx=
)dx=![]() Враховуючи
Враховуючи![]() dx =2, маємо
dx =2, маємо ![]() )dx=
)dx=
![]() =2+ х │
=2+ х │ ![]() =2+4+1=7 . Відповідь: В) 7.
=2+4+1=7 . Відповідь: В) 7.
- Оголошення теми, цілепокладань уроку.
- Ознайомлення з листом самооцінки . Виявлення в учнів очікуваних результатів.
Дата_________________,П.І.________________________
|
Теоретичні знання Бліц опитування Правильна відповідь 1б |
Кольоровий тест не помилився-2б, були помилки-1 б |
Огляд теоретичних знань до 4б |
СР 3,4 завдання-3б, 5*,6** завдання по 1б |
Загальна к-ть балів |
|
|
|
|
|
|
Девіз уроку: Узагальнення – це, мабуть, найлегший і найочевидніший шлях розширення математичних знань. В. Сойер
ІІ. Повторення, узагальнення й систематизація знань
- Бліцопитування
1. Поясніть, у якому випадку функція F(х) є первісною функції f(х) на проміжку . Навести приклад.
2.Сформулюйте основну властивість первісних. Проілюструйте її на прикладі(геометричний зміст первісних) Використати міні – презентацію «Графіки первісних» (додаток в електронному вигляді). 22
3. Дати означення невизначеного інтегралу.
4. Записати всі формули знаходження первісних, з використанням невизначеного інтегралу
5. Дати означення визначеного інтегралу, знання формули Ньютона-Лейбніца для обчислення визначених інтегралів.
2)Інтерактивна вправа «Кольоровий тест»
Використати підручник ,ст278 Тест «Перевір себе»(завдання 1-8) (Учні по команді піднімають колір картки з відповідною тестовою буквою a); b); c); d))
3) «Огляд теоретичних знань» з питань:
- Дати означення криволінійній трапеції. Ввести поняття визначеного інтегралу
- ** Доведення теореми . Площа S криволінійної трапеції, обмеженої графіком функції у= f(х) і прямими у=0, х=а і х=в (а˂в), можна обчислити за формулою S= F(b)-F(a),де F- будь-яка первісна функції f на відрізку [а;в ]
ІІІ. Удосконалення вмінь та навичок
Використати завдання Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень ,11 клас, ст.63 Завдання 3,4,*5,**6. Варіант1 або варіант 2.
Запропонувати виконати учням самоперевірку за листом самоконтролю.
ІV. Рефлексія. Протягом уроку діти заповнювали лист самооцінки.
Результати роботи на уроці визначимо «Райтингом» (це дріб, перша оцінка- оцінка учня,а в знаменнику оцінка вчителя, яку діти отримають на наступному уроці після перевірки зошитів). Чи задоволені результатом навчальних досягнень з теми. Бажаю Вам успіху на контрольній роботі.
V. Домашня робота. Завдання індивідуальні.( вчитель попередньо переглядає виконання домашніх завдань, робить виписки номерів або вправ які пропонує учню переробити)
Підготовка до КР
Урок 11. Тема: Контрольна робота «Первісна та інтеграл».
Цілепокладання: перевірити рівень навчальних досягнень учнів з даної теми.
Розвивати вміння швидко, логічно мислити, правильно висловлювати свої думки в письмовому вигляді.
Виховувати самостійність, відповідальність, наполегливість у досягненні мети.
Тип уроку: контролю знань, умінь, навичок.
І. Організаційний етап.
Учні готують зошити до роботи .
ІІ . Формулювання теми, мети і завдань уроку
Вчитель пояснює вимоги до виконання роботи. Використано Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень 11 клас ст.139-144 Завдання 1-9- рівнево. Варіант1 або 2 , 3, 4.
ІІІ. Виконання контрольної робота
ІV. Рефлексія 23
Відповідь на запитання: що в КР видалось вам найлегшим, а що найважчим?
V. Домашня робота
Завдання КР- паралельний варіант, рівнево до трьох прикладів на вибір. Повторити теорію теми.
Урок 12 Тема : Аналіз контрольних робіт. Розв’язування вправ.
Цілепокладання: провести аналіз рівня виконання контрольної роботи учнями класу, організувати корекційну роботу за блоком утруднень з теми, домогтися перерозв’яза-ння вправ з помилками, удосконалення навичків обчислювати інтеграли.
Формувати вміння самоаналізу.
Виховувати наполегливість у досягнення мети.
Очікувані результати: учні виправляють допущені помилки, обґрунтовують написане.
Обладнання: Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень 11 клас.
Тип уроку: корекції знань, умінь та навичок.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1) Перевірка наявності ДЗ .
2) Оголошення теми, ціле покладань уроку.
3)Отримання результатів контрольної роботи. Аналіз блоку утруднення.
ІІ. Практична робота
- Інтерактивна вправа «Мозковий штурм». Вчитель на дошці подає зразки вправ у яких найчастіше помилились учні. Обговорення помилок та корекція знань.
- Відпрацювання власних помилок (15 хв)
- Самостійна робота . Використано Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень 11 клас ст.145-147 Завдання 1-9- рівнево. Варіант 5-6.
ІІІ.Рефлексія. Самоперевірка результатів СР. Самооцінка навчальних досягнень на уроці.
Інтерактивна вправа «Вибери твердження».
Я відчув себе…
|
добре |
невпевнено |
комфортно |
|
безпорадним |
погано |
впевнено |
ІV. Домашнє завдання.
Перечитати П 26, звернути увагу на приклад 1,2. ** доведення теореми про площу криволінійної трапеції.
№26.2(Г',Д), №26.9*(3,4,5,8),**№26.20(1)
24
Література
- Збірник програм для до профільної підготовки та профільного навчання ( у двох частинах ) Частина ІІ. Профільне навчання. Навчальні програми для 10-11 класів загальноосвітніх закладів. Вид. «Ранок», 2011.
- Підручник А.Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський , М.С.Якір «Алгебра 11» Академічний, профільний рівень. Харків «Гімназія», 2011.
- Є.П.Нелін, О.Є. Долгова «Алгебра і початки аналізу.11 клас» Дворівневий підручник. Харків «Світ дитинства», 2008.
- Майстер - клас .О.М Роганін «Алгебра і початки аналізу». Плани - конспектів уроків.11 клас. Харків «Світ дитинства», 2002.
- Є.П.Нелін, О.М.Роганін «Зошит для поточного і тематичного оцінювання. Профільний рівень.11 клас. «Гімназія», 2011.
- Науково - методичний журнал «Математика в школах України» №33 2010,№5-6 2013, №31 2010, №12 2010,№7 2013, №34-36 2010, №9 2014.
25
Урок Акмеологічний урок алгебри в 11 класі. Тема: Розв’язування вправ з теми «Інтеграл».
Мета:
- закріпити вміння застосовувати таблицю первісних, правила інтегрування, використовувати набуті знання у фізиці, нагадати геометричний зміст первісної функції, перевірити навички обчислення визначеного інтегралу, знаходження площ криволінійних трапецій за поданим рисунком.
- Розвивати математичну мову, пам’ять, пізнавальний інтерес
- Виховання почуття відповідальності , вмінь працювати колективно.
Тип уроку: Урок закріплення знань, умінь, навичок.
Обладнання: картки для математичного диктанту, «Презентація «Геометричний зміст первісної функції»», матеріали для пазлу «Визначений інтеграл», зразки криволінійних трапецій для роботи в «Конструкторському бюро».
Структура, основний зміст, методи діяльності:
І. Організаційний етап.
Назвіть одним словом загальну тему, яку ми вивчаємо. ( Інтеграл)
Яких вмінь та навичок ми досягали протягом її вивчення? Де ми застосуємо вміння, отримані на цих роках.?
ІІ. Актуалізація опорних знань.
Вч. Урок почнемо з математичного диктанту, що активізує ваші знання таблиці первісних та правил знаходження невизначеного інтегралу.
Згадайте! Що називається невизначеним інтегралом?
Запишіть це у вигляді рівності (![]() (х) dх = F(х) +С )
(х) dх = F(х) +С )
Вч. Значення інтегралів - це 10 ключів до замка назви нашого уроку та відкриють двері до його завдань .
Отже, знайдіть первісні даних функцій
-
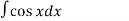 2.
2.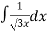
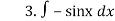
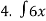 5 dx
5 dx 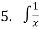 dх
dх 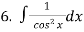 7.
7. 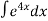 8.
8.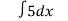 9.
9.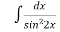
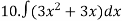
Вч. Встановіть відповідність між значенням інтегралів, № завдання та буквою, яку необхідно вписати за цим номером.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
а |
к |
м |
е |
о |
л |
о |
г |
і |
я |
Вч . Що допомогло нам відкрити замок. (Знання таблиці первісних та правил інтегрування)
ІІІ. Мотиваційний етап уроку.
Вч. Термін «акмеологія» походить від давньогрецького «акме» і визначається як «Вища точка, зрілість» (в дослівному перекладі «акме»- вершина, квітуча пора.) Греки словом «акме» називали період віку в людському житті, коли проявляється зрілість усього на що здатна ця людини.
Сьогоднішнім уроком підведемо підсумок знань , умінь, навичок з теми «Інтеграл» напередодні КР.
Пропоную Вам сходження сходинками « Піраміди досягнень» зійти на вершину «Акме».
Приготуйте листи самооцінення досягнень на кожній сходинці піраміди.
П.І. учня_____________________ Дата __________клас_________
|
МД 2б |
Алгебра + фізика mak 3б |
ГЗП Презентація 1б |
Пазл «Інтеграл» mak 3б |
Конструкторське бюро mak 3б
|
|
|
|
|
|
|
Самооцінення: кількість ______балів
IV. Застосування знань, умінь, навичок.
1сходинка. І етап. Пригадайте де у фізиці ми можемо застосувати знання знаходження первісної функції.
( - інтегрування функції по швидкості маємо рівняння руху тіла, інтегруючи прискорення знаходимо швидкість руху тіла в момент часу…)
Пропоную Вам застосувати знання теми «Інтеграл» у фізиці.
Підручник А.Г. Мерзляк, Д.А.Номіровський, Харків «Гімназія» 2011, Алгебра профільний рівень, 11 клас. * № 25.12.
( учні середнього рівня користуються карткою – алгоритмом виконання роботи)
( 1 учень виконує роботу на дошці для самоперевірки).
Вчитель контролює виконання роботи. Учні перевіряють виконання роботи, уточнюють недоліки. Виставляють бали в листах самооцінки( учні, які користувались листами- алгоритмами – 1б, не повний розв’язок- 2б, повне пояснення- 3б).
ІІ етап
Учні протягом вивчення теми виконували проектну роботу «Геометричний зміст первісної».
Вчитель пропонує презентувати деякі роботи.
Самооцінка результатів дослідження (1б)
2 сходинка
Вч. Вміння знаходити визначений інтеграл дасть можливість зіграти в пазл
« Визначений інтеграл».
Виберіть частини пазлів, які відповідають розв’язкам даних інтегралів та складіть частинки. На іншій стороні матимемо малюнок.
Кількість балів відповідатиме кількості вірно розв’язаних інтегралів. За час відведений на роботу потрібно встигнути заробити більше балів.
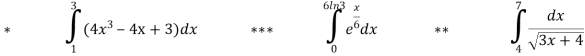
Вчитель надає допомогу, консультує окремих учнів.
По завершенню часу виконання роботи учні знаходять на частинах пазлів правильні відповіді і складають пазл. На іншій стороні пазлу учні знайдуть портрети вчених, формулою яких користувались під час роботи з визначеним інтегралом.
Запишіть формулу Ньютона -Лейбніца. ( 1 учень біля дошки)
Поставте бали до листа самооцінки.
ІІІ сходинка. «Конструкторське бюро»
Вч. - Де на практиці застосовується визначений інтеграл.( Знаходження площі криволінійної трапеції)
- Що називаємо криволінійною трапецією?.
- Уявіть себе працівниками конструкторського бюро. Надійшло три замовлення на виготовлення ескізів залізних воріт для дачного подвір’я.
- Утворюємо три фірми, які беруть відповідальність виконання замовлення за таким планом.( учні знайомляться з вимогами роботи в групі, розподіляють обов’язки).
Учні виконують роботу: до поданих малюнків необхідно правильно записати визначений інтеграл для знаходження площі криволінійної трапеції, що є площею однієї сторони воріт, збільшити площу вдвічі, застосувати масштаб, вирізати макет, розмалювати його, приготуватись до презентації роботи.
Підручник № 26.1 малюнки а, в, г.
Після презентації учні виставляють бали в листи самооцінки.
IV. Підсумок уроку.
- Рефлексія.
Вч. Ось ми і на вершині піраміди знань. Визначте своє «Акме». Який результат роботи на уроці. Чи задоволені ви роботою, покажіть це в листі самооцінки смайликом настрою.
Вч. Наступним уроком ви пишете КР. Надіюсь ви отримаєте бажаних результатів.
А закріпити вміння вам допоможе ДР.
- Домашнє завдання: Підручник. Підручник А.Г. Мерзляк, Д.А.Номіровський, Харків «Гімназія» 2011, Алгебра профільний рівень, 11 клас.
Повторити таблицю первісних, правила інтегрування.
№26.3(парні), *26.1(е)
Д+В №26.5(1), *26.9(непарні), ** 26.20(2)
Урок завершено.Бажаю успіхів на КР.
Урок Тема: Розв’язування вправ
Мета: узагальнити та систематизувати знання із теми «Інтеграл та його застосування»; провести огляд типових задач із зазначеної теми; удосконалювати вміння розв’язувати задачі, що передбачають обчислення площ плоских фігур , об’ємів тіл за допомогою визначеного інтегралу;
розвиток навиків самооцінення результатів роботи на уроці;
розвиток вмінь користуватись програмою «Графічний калькулятор» для побудови графіків функцій.
Обладнання: картки усного рахунку, малюнки криволінійних трапецій, комп’ютери, програма «Графічний калькулятор».
Хід уроку.
І. Організаційний етап.
Назвіть одним словом загальну тему, яку ми вивчаємо. ( Інтеграл)
Яких вмінь та навичок ми досягали протягом її вивчення? Де ми застосуємо вміння, отримані на цих уроках.?
Оголошення теми, завдань уроку.
ІІ Мотивація
Сьогоднішнім уроком підведемо підсумок знань , умінь, навичок з теми «Інтеграл» напередодні КР.
Пропоную Вам сходження сходинками « Піраміди досягнень» зійти на вершину знань, умінь та навичок.
Приготуйте листи самооцінення досягнень на кожній сходинці піраміди.
П.І. учня_____________________ Дата ________клас_________
|
Формули 2б |
Обчислення інтегралів 2б |
Вміння використовувати ком. програми 2б |
Обчислення площ 2б |
Обчислення інтегралів 2б |
Додатково Завдання ** 2б |
|
|
|
|
|
|
|
Самооцінення: кількість ______балів
ІІІ. Практична частина.
- Формули.
|
Збирач формул |
Самодиктант формул |
|
Учень використовує картки та складає формули обчислення невизначених інтегралів |
Учні на окремих листах відтворюють формули обчислення невизначених інтегралів. |
Учні здійснюють самоперевірку формул, виставляють бали в листку самооцінення.
- Етап обчислення визначених інтегралів.
- Етап застосування визначеного інтегралу для обчислення площ плоских фігур. Використання програм «Графічний калькулятор» та «Paint».
Учні будують графіки функцій, виділяють фігуру площу якої необхідно знайти. В робочому зошиті обчислюють площу фігури.
- Етап застосування визначеного інтегралу для знаходження об’ємів тіл, отриманих в результаті обертання криволінійних трапецій або в результаті обертання плоскої фігури.
На кожному етапі учні ведуть листи самооцінки досягнень.
- Застосування інтегралу у фізиці.
IV. Підсумок уроку.
- Рефлексія.
Вч. Ось ми і на вершині піраміди знань. Визначте свій рівень досягнень. Який результат роботи на уроці. Чи задоволені ви роботою, покажіть це в листі самооцінки смайликом настрою.
Вч. Наступним уроком ви пишете КР. Надіюсь ви отримаєте бажаних результатів.
А закріпити вміння вам допоможе ДР.
- Домашнє завдання: Підручник. Підручник А.Г. Мерзляк, Д.А.Номіровський, Харків «Гімназія» 2011, Алгебра профільний рівень, 11 клас.
Повторити таблицю первісних, правила інтегрування.
№26.7, *26.6(6)
** 26.20(2)
Урок завершено.Бажаю успіхів на КР.
Урок 23 Тема: Контрольна робота «Інтеграл і його застосування».
Мета уроку: перевірити й оцінити рівень навчальних досягнень учнів з даної теми.
Тип уроку: контролю знань, умінь, навичок.
І. Організаційний етап.
Учні готують зошити до роботи .
ІІ . Формулювання теми, мети і завдань уроку
Вчитель пояснює вимоги до виконання роботи. Використано Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень 11 клас ст.148-153 Завдання 1-9 рівнево. Варіант1 або 2 , 3, 4.
ІІІ. Контрольна робота
ІV. Підбиття підсумків. Домашня робота: Завдання КР паралельний варіант. Рівнево до трьох прикладів. Повторити теорію теми
Урок 24 Тема : Аналіз контрольних робіт. Розв’язування вправ.
Цілепокладання: провести аналіз виконаних робіт всього класу, корекцію знань, домогтися перерозв’язанню вправ з помилками, розвиток навичок обчислювати інтеграли.
Структура, основний зміст, методи діяльності:
І. Мотиваційно- організаційний етап
1) Перевірка наявності ДЗ .
2) Оголошення теми, плану роботи.
Отримання результатів контрольної роботи.
ІІ. Практична робота
- Інтерактивна вправа «Мозковий штурм». Вчитель на дошці подала зразки вправ у яких найчастіше помилились учні. Обговорення помилок та корекція знань.
- Відпрацювання власних помилок (15 хв)
- Самостійна робота . Використано Збірник Є.П.Нелін «Зошит для поточного і тематичного оцінювання» Профільний рівень 11 клас ст.154-156 Завдання 1-9 рівнево. Варіант 5-6.
ІІІ.Рефлексія. Самоперевірка результатів СР. Самооцінення.
ІV. Домашнє завдання. Перечитати П 26, звернути увагу на приклад1,2. ** доведення теореми про площу криволінійної трапеції.
№26.2(Г',Д), №26.9*(3,4,5,8),**№26.20(1)
-
-
Дякую.
-
Дякую.


про публікацію авторської розробки
Додати розробку
