Розробка уроку на тему «Застосування комбінаторних формул для обчислення ймовірностей подій».

Про матеріал

Мета уроку:

-сформувати в учнів вміння використовувати формули комбінаторики для обчислення ймовірності події;

-розвивати вміння аналізувати, робити висновки, пам 'ять, увагу, обчислювальні навички; формувати життєві компетенції учнів;

-виховувати інтерес до математики, наполегливість, впевненість у своїх силах;

-показати групові та колективні форми роботи при формуванні вмінь та навичок учнів.

Перегляд файлу

Розробка уроку на тему

«Застосування комбінаторних формул для

обчислення ймовірностей подій».

$C:\Documents and Settings\Admin\Мои документы\карт матем\теория-вероятностей-210x300.jpg$

Викладач Токар С. М.

Тема уроку. ЗАСТОСУВАННЯ ФОРМУЛ КОМБІНАТОРИКИ ДЛЯ ОБЧИСЛЕННЯ ЙМОВІРНОСТЕЙ ПОДІЙ.

Мета уроку:

сформувати в учнів вміння використовувати формули комбінаторики для обчислення ймовірності події;
розвивати вміння аналізувати, робити висновки, пам ‘ять, увагу, обчислювальні навички; формувати життєві компетенції учнів;
виховувати інтерес до математики, наполегливість, впевненість у своїх силах;
показати групові та колективні форми роботи при формуванні вмінь та навичок учнів.

Обладнання: опорні схеми для розв’язування комбінаторних задач,кубики з назвами випробувань і відповідних подій, сигнальні картки «Види подій», скринька з різнокольоровими прямокутниками.

Тип уроку: застосування знань, вмінь і навичок.

ПЛАН ПРОВЕДЕННЯ.

І. Організаційний етап.

ІІ. Перевірка домашнього завдання.

Вступне слово. Тема нашого уроку буде сформульована після перевірки домашнього завдання. Вдома вам потрібно повторити основні терміни, що були вивчені на попередніх уроках.

Для того, щоб зрозуміти тему уроку і дізнатися, які задачі будуть розв’язуватися на цьому уроці, розглянемо кросворд.

Робота в парах.

З допомогою слів – підказок вгадати ключове слово кросворду.

ПО ВЕРТИКАЛІ:

Будь – яке явище, що може відбутися або не відбутися у результаті експерименту.
Подія, яка внаслідок даного випробування не може відбутися.
Умови, в результаті яких відбувається ( чи не відбувається) подія.
Подія, яка внаслідок даного випробування обов’язково відбудеться.
Відношення числа подій, які сприяють виконанню даної події, до загальної кількості подій простору елементарних подій.
Подія, яка може відбутися або не відбутися під час даного випробування.
Видатний французький математик, що разом з Паскалем запровадив поняття ймовірності.
Випробування – підкидання грального…

				5
		3

					6		8
	2					7
1			4

Відповіді до кросворду.

ПО ВЕРТИКАЛІ:

Подія.
Неможлива.
Випробування.
Вірогідна.
Ймовірність.
Випадкова.
Ферма.
Кубика.

ПО ГОРИЗОНТАЛІ:

КОМБІНАТОРИКА

Додаткові запитання.

Які задачі називають комбінаторними?
Який розділ математики називається комбінаторикою?
Які скінчені множини розглядають при розв’язуванні комбінаторних задач?

Доповідь учня про історію виникнення та розвиток теорії ймовірностей.

ІІІ. Формулювання теми і мети уроку.

Мотивація навчальної діяльності.

Ви помітили, що в цьому кросворді переплетені поняття з двох розділів математики: теорії ймовірностей і комбінаторики. А тема уроку звучить як Застосування елементів комбінаторики для обчислення ймовірностей подій. І у вас є можливість навчитися розв’язувати актуальні задачі, пов’язані з обраною професією та реальним життям.

ІV. Актуалізація опорних знань.

Викликаються 3 учня, вони повинні встановити відповідність ВИПРОБУВАННЯ→ПОДІЯ→ВИД ПОДІЇ (дані містяться на 2 кубиках і сигнальних картках:

І ВИПРОБУВАННЯ:

1) Підкидання монети.

2) Жеребкування команд з футболу на розіграші кубку УЄФА.

3)Дивимось на аркуш відривного календаря.

4) Виймаємо деталь з ящика.

5)Набираємо букви С, И, Р в довільному порядку.

6) Нагрівання дроту.

ІІ 1) Написано слово РИС.

2) Бачимо дату 30 лютого.

3) Динамо попадає в групу А.

4) Довжина дроту збільшилась.

5) Деталь бракована.

6) Випав герб.

ІІІ Сигнальні картки.

1) Випадкова.

2 ) Вірогідна.

3) Неможлива.

Оцінюється робота викликаних учнів.

V. Формування вмінь та навичок .

Фронтальне виконання усних вправ.

Знайдіть імовірність того, що ваш знайомий народився у неділю?
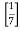
Як з латинської перекладається слово факторіал ? [ множник]
Обчисліть 4! [1·2·3·4=24]
Чому дорівнює ймовірність вірогідної події ? неможливої події ?[1;0]
У меню їдальні є 3 перші страви, 6 других і 4 треті страви.

1)Скількома способами можна обрати 1 страву?

2) Скількома способами можна обрати обід, який містить по одній страві кожного виду ?

( Обрати правильну відповідь до кожного запитання)

А) 13; Б) 36; В) 72; Г) 54

[А) – правило суми,В) – правило добутку]

Що ймовірніше вгадати: 3 числа з 49 чи 4 числа з 36 ? [4 з 36]
Під час перевірки готової продукції виявляють брак за формою та розмірами. Ймовірність браку за формою дорівнює 0,05, а за розмірами – 0,01. Яка ймовірність того, що взята навмання деталь буде бракованою і за формою, і за розмірами?[Яке правило: суми чи добутку слід використати ? За правилом добутку: 0,01·0,05=0,0005]

Колективне розв’язування письмових задач під керівництвом вчителя.

1. Скількома способами із 9 членів комісії можна вибрати голову,заступника і секретаря ?

[]або

У футбольній команді, яка складається з 11 гравців, потрібно вибрати капітана та його заступника. Скількома способами це можна зробити?[

2. Набираючи номер телефону, абонент забув 2 останні цифри і, пам’ятаючи лише, що ці цифри різні,набрав їх навмання. Яка ймовірність того, що номер набрано правильно ?

[Загальна кількість елементарних подій випробування: вибираємо 2 цифри з 10-це розміщення з 10 елементів по 3. Кількість елементарних подій, які сприяють виконанню події В –«номер набрано правильно», дорівнює 1. Отже, Р(В)= ]

3. Після успішного написання ЗНО з математики, п’ятеро щасливих учнів здійснили подорож до Чорного моря, замовивши для цього автомобіль з водієм на 5 пасажирських місць. Господар автомобіля запропонував їм такий відпочинок щороку і кожного разу сідати у той самий автомобіль по – іншому. Після того, як усі способи будуть вичерпані, їх возитимуть безкоштовно. Через скільки років настане цей щасливий день?

[Потрібно розмістити 5 різних учнів на 5 різних місць: років]

4. В коробці по 3 червоних, 7 зелених і 10 жовтих прямокутників однакового розміру. Навмання виймають 1. Яка ймовірність того, що навмання вийнятий прямокутник буде жовтого кольору?[Всього в коробці 20 прямокутників. Число способів вийняти 1 з 10 жовтих дорівнює 10. Р(А)=]

ЕКСПЕРИМЕНТ: ВИЙМАЄМО 10 ПРЯМОКУТНИКІВ НАВМАННЯ . Чи дорівнює ймовірність виймання жовтого прямокутника ?)

5.Учасник спортлото виграє, якщо вгадає 6 чисел із запропонованих 45. Знайдіть ймовірність виграшу.

[Число можливих комбінацій, враховуючи те, що порядок вгаданих чисел не враховується, дорівнює: (Загальне число подій.)

Число подій, що сприяють виконанню події А-«вгадано 6 чисел із 45» -1.

За класичним означенням ймовірності:

Р(А) =]. Висновок. Чи варто грати в лотереї ?

А чи настільки примарною є можливість виграти в лотерею ?

В 1992 році група австралійських однодумців об’єдналася, щоб виграти в лотерею, в якій потрібно було вгадати 6 із 44 комбінацій ( типу СПОРТЛОТО). Призовий фонд складав 27 мільйонів доларів, а різних комбінацій було близько 7 мільйонів. В результаті кожен витратив на білети по 2500 доларів і закрасивши всі можливі комбінації, вони виграли всі 27 мільйонів і кожний отримав по 9000 доларів.

V. Домашнє завдання.

Розв’язати задачу.

Людина забула пін –код свого мобільного телефону, який складається з 4 цифр. Проте людина пам’ятає, що всі цифри коду різні. Яка ймовірність того, навмання набрані 4 цифри будуть правильними?

Додаткове завдання.

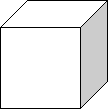
Для обчислення ймовірностей часто використовується випробування: ПІДКИДАННЯ ГРАЛЬНОГО КУБИКА. На рисунку зображено гральний кубик. Скільки очок на його зафарбованій грані ? Відповідь: 1(сума очок на протилежних гранях куба дорівнює 7).