Розв’язання цілих раціональних рівнянь різними способами

 

 

 

 

 

 

Розв’язання цілих раціональних рівнянь різними способами

 

 

 

                                              Статтю підготувала вчитель математики

                                              Черкаського фізико-математичного ліцею (ФІМЛІ)

                                              Черкаської міської ради Черкаської області

                                              Темченко М. В.

 

 

 

 

 

 

 

 

 

Черкаси-2021

При вивченні математики не хотілося б обмежуватися лише простим вивченням програми та результатом навчання. Потрібен аналіз вимог до шкільної програми. Перш за все вчителю необхідно врахувати інтереси учнів старших класів, яким потрібна підготовка до ЗНО. Тобто необхідність вивчення нових тем з алгебри й початків аналізу. Однією з них є тема: «Многочлени», у який розглядаються рішення рівнянь вищих порядків. Вивчення цієї програми:

1. Дає змогу вчителю розширити застосування функцій, що вивчаються  та їх властивостей.
2. Дає учням інструмент для повного дослідження функцій, що є многочленами, з показником степеню вище двох.
3. Дає учням змогу узагальнити й систематизувати вивчені раніше матеріали, об’єднати всі окремі випадки в одне ціле.

При підготовці розробки даної теми були пройдені такі етапи.

1. Вивчення програми з математики з урахування вимог учнів старших класів.
2. Методи розв’язування й підбір задач.
3. Методичне опрацювання основних теорем.
4. Вибір алгоритмів розв’язку стандартних задач.

В програмі з поглибленим вивченням математики за 8 клас на дану тему годин явно недостатньо, оскільки ця тема є базовою для багатьох наступних тем: розв’язування тригонометричних, логарифмічних рівнянь, дослідження функцій та інше. У результаті вивчення цієї статті читач повинен навчитися розв’язувати різні типи рівнянь вищого порядку різними способами:

1. Використання схем Горнера.
2. Розкладання на множники.
3. Підбір цілочислового кореня.
4. Графічний метод.
5. Використання властивостей функцій.
6. Розкладання на множники з урахуванням найденого цілого кореня без ділення кутом.
7. Використання властивостей множення.
8. Застосування похідної до розв’язування рівнянь.

 

В статті розглянуті приклади декількох рівнянь, розв’язаних різними способами, а також розв’язання одного рівняння шістьома способами. Також розглянемо “нестандартні” рівняння.

В кінці статті є добірка рівнянь для самостійного розв’язування (з відповідями), деякі з них можна запропонувати учням розв’язати різними способами.

Розкладання лівої частини на множники (права частина дорівнює нулю) досить розповсюджений прийом розв’язування рівнянь. Тут немає єдиного підходу. Багато залежить від вміння та досвіду. Тому пропонуються інші способи.

При розв’язуванні цілих раціональних рівнянь перетворення, що виконуються, приводять до рівносильного рівняння. Тому, знайдені корені не перевіряють.

Шостий спосіб розв’язування одного з прикладів зацікавить учнів старших класів, так як для цього способу необхідні знання похідної та її застосування.

 

Різні способи розв’язування цілого раціонального рівняння

 

1. Застосовуючи схему Горнера
2. Метод ділення многочлена “кутом”
3. Графічний метод
4. Метод заміни змінних
5. Застосування властивостей многочлена
6. Застосування похідної до розв’язування рівнянь

 

              Цілі раціональні рівняння

Рівняння виду:

1. 

(n N, 0) є алгебраїчне рівняння степені n.

 

2. називається зведеним цілим раціональним рівнянням.

Теорема1: Якщо зведене ціле раціональне рівняння з цілими коефіцієнтами має раціональний корінь, то цей корінь є ціле число.

Теорема2: Якщо ціле раціональне рівняння з цілими коефіцієнтами має цілі корені, то вони являються дільниками вільного члена.

Приклад 1. Розв’язати рівняння:

Розв’язання:

Випишемо дільники вільного члена і перевіримо, який з них буде коренем:

,

є коренем. Поділимо на , тим самим зменшивши степінь рівняння. Для знаходження застосуємо схему Горнера:

 

	1	-4	-13	28	12
2	1	-2	-17	-6	0

                

Отже, можна записати, що:

     

Із першого рівняння сукупності знаходимо:

,

Для другого рівняння виписуємо дільники вільного члена: 6 кратне:

Числа не можуть бути коренями рівняння  , так  як вони не були коренями рівняння 

Корінь може бути кратний, тому його знову потрібно перевірити:

є коренем. Розділивши понизимо степінь на одиницю:

 

	1	-2	-17	-6
-3	1	-5	-2	0

Отже,

                      

Запишемо корені

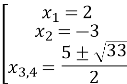
 Відповідь: .

Приклад 2. Розв’яжемо рівняння:

  

Використовуючи необхідну умову існуючого цілочислового кореня, винесемо дільники вільного члена:

Перевіркою дізналися 

За теоремою Бізу початковий многочлен ділиться націло на  (х-2).

Виконаємо ділення:

;

Таким чином многочлен

Аналогічно розв’яжемо рівняння: ;

;

Початкове рівняння можна записати так:

() = 0

        

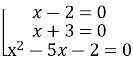
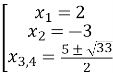
Відповідь: .

Приклад 3. Розв’язати рівняння:

;

Розв’язання: помножимо ліву частину на 2 і отримаємо:

  ;

Заміна 2х=t;

;

Розв’яжемо рівняння відносно t. Перевіркою дізнаємось, що t=1 є коренем рівняння:

                  система має один дійсний корінь .

А початкове рівняння має єдиний дійсний корінь ;

Відповідь:.

Приклад 4. Розв’язати рівняння:

;

Розділимо обидві частини рівняння на ( не є коренем рівняння)

;

Заміна ;

Отримаємо рівняння:

                       

Повернемося до заміни:

                   

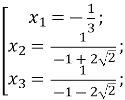
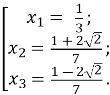
Відповідь: .

 

Приклад 5. Розв’яжемо одне рівняння 6 різними способами:

1 спосіб:

Розкладемо ліву частину на множники. Маємо:

Останнє рівняння рівносильне сукупності рівнянь:

;

Корінь першого рівняння Друге рівняння дійсних коренів не має.

2 спосіб:

Розв’яжемо рівняння:

;

Методом підбору знайдемо цілий корінь рівняння. Застосуючи необхідну умову  існування цілочислового кореня, винесемо дільники вільного члена:

                     ;

Таким чином   - корінь рівняння;

Використовуючи, що  многочлен

Виконаємо ділення:

Таким чином

а початкове рівняння має вигляд:

Відповідь:                     

3 спосіб:

Розв’яжемо рівняння:   ;

Пишемо рівняння:  

Розглянемо функції:    

Функція      є зростаючою;

Функція     є спадною;

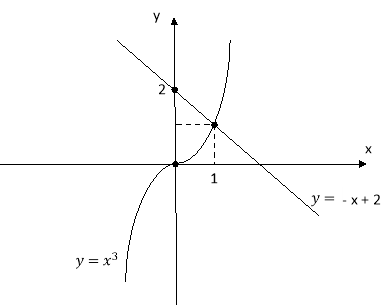Тому графіки даних функцій мають не більше однієї спільної точки. Знайдемо підбором цю точку:

;

Відповідь:

 

                                                                                                             

                                                                              

                                                                                                           

  

 

 

4 спосіб:  Розглянемо ще один спосіб розв’язування даного рівняння

Нехай  P(x) =

P(1) =

Знайдемо різницю P(x) і P(1)

P(x)P(1)=

Розкладемо праву частину на множники

P(x) P(1) == ( 1)(

Так як P(1) = 0

P(x) = ( 1)(

( 1)(

( 1)

Відповідь: x = 1.

 

5 спосіб:  Розв’яжемо рівняння , застосуючи похідну функції

Розглянемо функцію y =

Знайдемо похідну цієї функції

y =

Так як похідна приймає тільки додатні значення, функція зростає на множині дійсних чисел. Тому існує тільки одна точка перетину графіка функції y = з віссю абсцис.

Знайдемо її: x=1

Відповідь: x = 1.

Це є відповідь цього рівняння.

 

6 спосіб:  Можна розв’язати дане рівняння, застосовуючи схему Горнера.

 

Приклад 6:  Розв’язати рівняння з двома змінними

Сума двох  чисел дорівнює  нулю  тоді  і  тільки тоді, коли кожне з них дорівнює 0.

Тому x = 3; y = 2.

 

 

Задачі для самостійного розв’язання

 

1		{-2}
2		{-0-}
3		x=2
4		{-0-}
5		{±1}
6		{-1;-3;-5;}
7		{1;2;2.5;5}
8		{1;2}
9		{-0-}
10		{-4;±}
11		{-1}
12		{-}
13		{-}
14		{}
15		{}