Розв’язування квадратних рівнянь. Презентація.
Про матеріал
Мета уроку:
Сформувати в учнів вміння застосовувати знання про квадратні рівняння під час розв’язування вправ; перевірити рівень засвоєння знань учнів з даної теми;
виховувати вольову сферу особистості: рішучість, самостійність, цілеспрямованість, сміливість, витримку; вміти оцінювати свої знання;
розвивати творчі здібності учнів, математичне мислення , розвивати вміння працювати в групі, виступати перед аудиторією.
Перегляд файлу
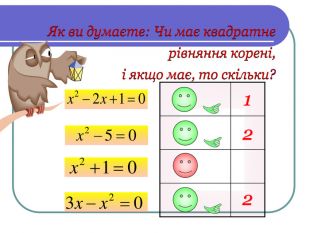
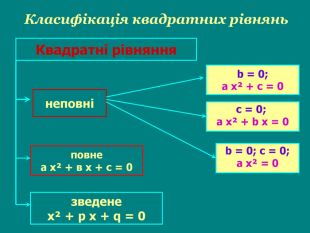
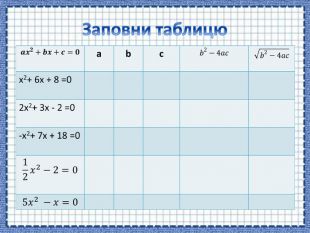
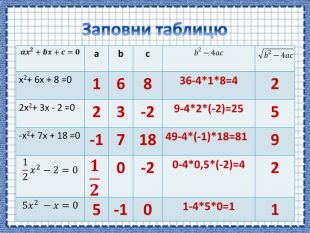
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Чудова робота. Дякую.
-
pptx
До підручника
Алгебра 8 клас (Істер О. С.)
До уроку
Розділ 3. Квадратні рівняння Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку