Розв'язання системи рівнянь та нерівностей з параметрами.
Матеріал містить розв'язання систем рівнянь та нерівностей з параметрами графічним методом в системі хОа. та їх графічну ілюстрацію. Завдання № 20.23 та №20.25 з підручника Алгебра 9кл Автори А.Г Мерзляк, В.Б.Полонський, М.С. Якір Підручник для класів з поглибленим вивченням математики.
Алгоритм розв’язування завдань графічним методом в системі хОу.
- Знаходимо область визначення рівняння.
- Запишемо рівняння у вигляді f(x)=g(x) .
- У системі координат хоу будуємо графіки функції у=(х) та у=g(x) для тих значень х, які входять в область визначення даного рівняння.
- Встановлюємо взаємне розташування графіків даних функцій в залежності від значень параметра а.
- Якщо графіки перетинаються, то визначаємо абсциси точок перетину. Для цього достатньо розв'язати рівняння (х) = g(x) відносно х.
- Записуємо відповідь.
Алгоритм розв’язування завдань графічним методом в системі хОа.
- Знаходимо область визначення рівняння.
- Виражаємо a як функцію від х.
- У системі координат хоа будуємо графік функції а=(х) для тих значень х, які входять в область визначення даного рівняння.
- Знаходимо точки перетину прямої а = с, де с(-;+) з графіком функції а=(х). Якщо пряма а = с перетинає графік а=(х), то визначаємо абсциси точок перетину. Для цього достатньо розв'язати рівняння а=(х) відносно х.
- Записуємо відповідь.
Зауваження. В системі хОа зручно розв’язувати рівняння , нерівності та їх системи, якщо вирази містять неявні функції. Наприклад: рівняння кола, квадрата та ін. тоді в одній системі координат будуємо графіки заданих рівнянь, нерівностей, встановлюємо залежність кількості розв’язків та їх значення в залежності від значень параметра а.
Нерівності з параметрами
Алгоритм розв’язування.
1. Знаходимо область визначення даної нерівності.
2. Зводимо нерівність до рівняння.
3. Виражаємо а як функцію від х.
4. В системі координат хоа будуємо графіки функцій а = f (х) , або графіки рівнянь f(x,a)=0 для тих значень х, які входять в область визначення даної нерівності.
5. Знаходимо множину точок, які задовольняють даній нерівності.
6. Досліджуємо вплив параметра на результат:
• знайдемо абсциси точок перетину графіків.
• задамо пряму а =с (с- соnst) і будемо зрушувати її при![]()
7. Записуємо відповідь.
Це всього лише один з алгоритмів розв'язання нерівностей з параметрами, з використанням системи координат хоа. Можливі й інші методи рішення, з використанням стандартної системи координат хоу.
Приклади.
Приклад 1. Знайти розв’язки нерівності ![]() при всіх допустимих значеннях параметра а.
при всіх допустимих значеннях параметра а.
Розв’язок.
Знайдемо корені тричлена в лівій частині нерівності:
х1=-2а+1; х2=3а.
Розкладемо тричлен на множники:
(х+2а-1)( х-3а)≥0
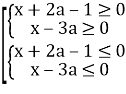 ;
;  .
.
Прямі, задані рівняннями х=-2а+1; х=3а, розбивають координатну площину хоа на чотири області, в кожній з яких квадратний тричлен х2-(а+1)х-6а2+3а зберігає постійний знак.
Знайдемо ординату точки перетину прямих х=-2а+1; х=3а: а=0.2.
Задамо пряму а =с (с- соnst) і будемо переміщати її при![]() .
.
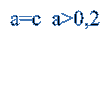
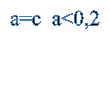
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
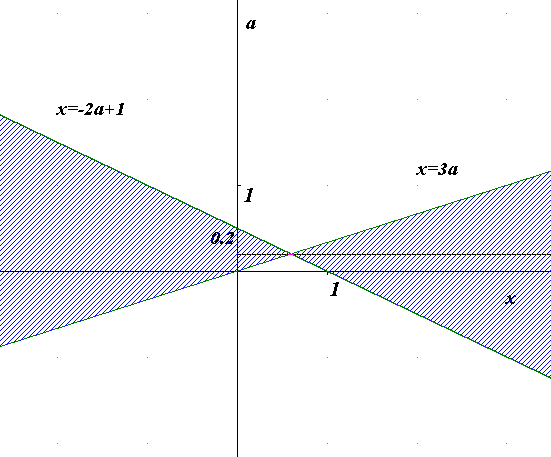
Проаналізуємо взаємне розташування графіка нерівності
х2-(а+1)х-6а2+3а>0 та прямих а =с при![]() записуємо розв’язки даної нерівності.
записуємо розв’язки даної нерівності.
Маємо: ![]()
при ![]() .
. ![]()
![]() ;
;
при ![]() .
. ![]()
![]() ;
;
при а=0.2 ![]() .
.
Відповідь:
при ![]()
![]()
![]() ;
;
при а=0.2 ![]() ;
;
при ![]()
![]()
![]() .
.
ІV. Системи рівнянь та нерівностей з параметрами.
Приклад 1. . (№20.23 Алгебра 9кл Автори А.Г Мерзляк, В.Б.Полонський, М.С. Якір Підручник для класів з поглибленим вивченням математики)
При яких значеннях параметра а має розв’язки система
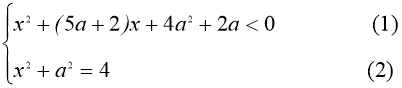
Розв’язок.
Знайдемо корені тричлена в лівій частині нерівності (1) ![]() .
.
Прямі, задані рівняннями 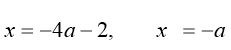 ,
,
розбивають координатну площину хоа на чотири області, в кожній з яких квадратний тричлен
![]() зберігає постійний знак.
зберігає постійний знак.
![]()
![]()
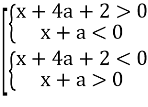 ;
; 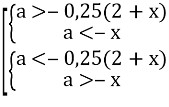 .
.
Розв’язком нерівності будуть виділені області площини.
![]()
![]()
Рівняння (2) задає коло радіуса R=2 з центром y початку координат.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Тоді розв’язком вихідної системи буде перетин заштрихованої області з колом. Система має розв’язки при![]()
Значення![]() і
і![]() знаходяться з системи
знаходяться з системи
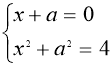 ;
; 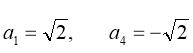 ,
,
а значення а2 і а3 знаходяться з системи
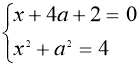 ;
; 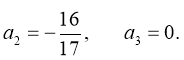
Отже система має розв’язки при ![]()
Відповідь: ![]()
Приклад 2. (№20.25 Алгебра 9кл Автори А.Г Мерзляк, В.Б.Полонський, М.С. Якір Підручник для класів з поглибленим вивченням математики)
При яких значеннях параметра а система нерівностей
![]() має:
має:
- розв’язки;
- єдиний розв’язок;
- тільки від’ємні розв’язки;
- тільки додатні розв’язки;
-
тільки розв’язки, що задовольняють умову
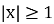 ;
;
- множину розв’язків, що містить не більше одного цілого числа?
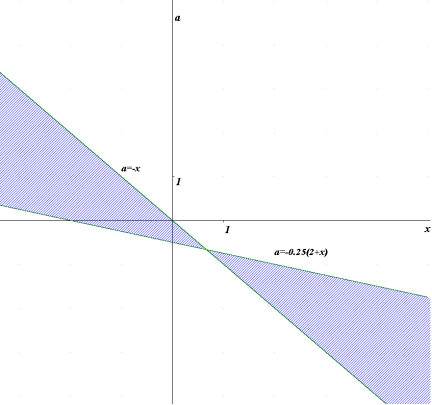
Побудуємо графік кожної нерівності в системі хоа та знайдемо множину точок координатної площини, координати яких є розв’язками даної системи нерівностей.
Для побудови графіка![]() побудуємо графік
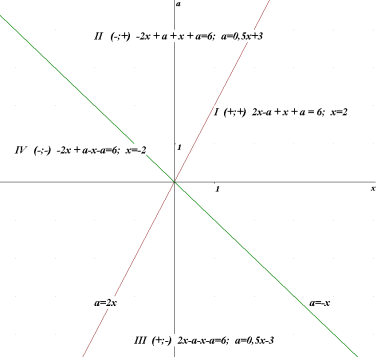
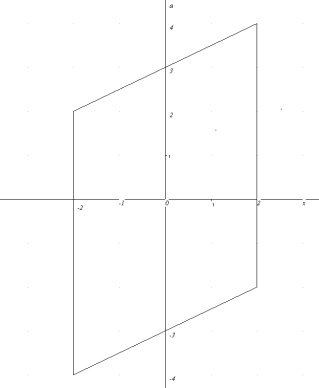
побудуємо графік ![]() . Прямі, задані рівняннями 2х-а=0 та х+а=0, розбивають координатну площину хоа на чотири області, в кожній з яких вирази 2х-а та х+а зберігають постійний знак. Розкриваючи модулі в кожній області, отримаємо рівняння прямих, які разом є рівнянням
. Прямі, задані рівняннями 2х-а=0 та х+а=0, розбивають координатну площину хоа на чотири області, в кожній з яких вирази 2х-а та х+а зберігають постійний знак. Розкриваючи модулі в кожній області, отримаємо рівняння прямих, які разом є рівнянням ![]() .
.
![]()
![]()


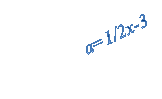
![]()
![]()
![]()
![]()
![]()
![]()
![]() Виділимо область, яка є розв’язком нерівності
Виділимо область, яка є розв’язком нерівності![]()
![]()

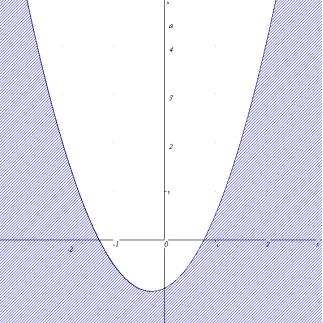
Графіком нерівності![]() є частина площини хоа, обмежена параболою а=х2+0,5х-1.
є частина площини хоа, обмежена параболою а=х2+0,5х-1.
![]()
![]()
![]()
Графік даної системи нерівностей:
![]()
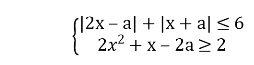
![]()
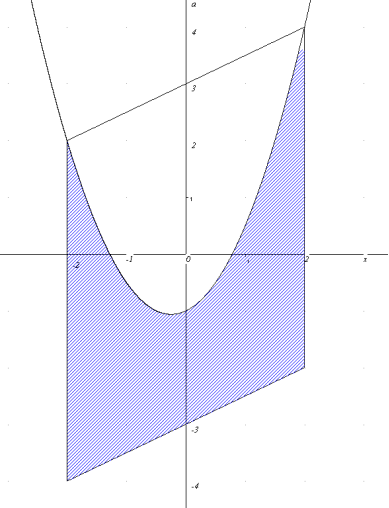
Відповіді на запитання задачі:
-
Система нерівностей має розв’язки при
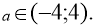
![]()
![]()
![]()
![]()
![]()

- Система має єдиний розв’язок х=-2 при а=-4 та х=2 при а=4.
-
Система має тільки від’ємні розв’язки
 при
при 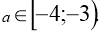
![]()
![]()
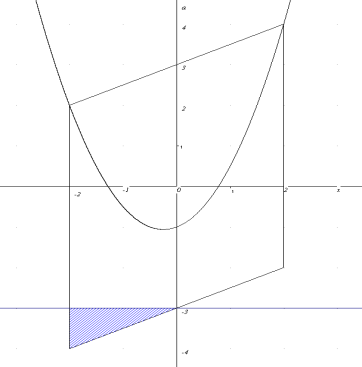
-
Система має тільки додатні розв’язки
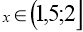 при
при 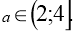
![]()
![]()
![]()
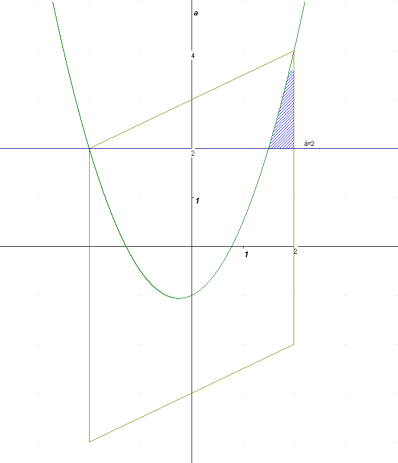
Значення х для даної умови знайдемо з системи:
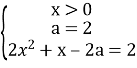 ;
; 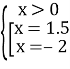 ;
; ![]()
-
Система має тільки розв’язки, що задовольняють умову
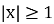
Побудуємо графік системи нерівностей:
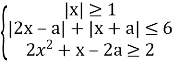
![]()
![]()
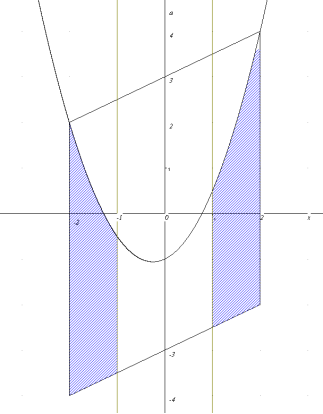
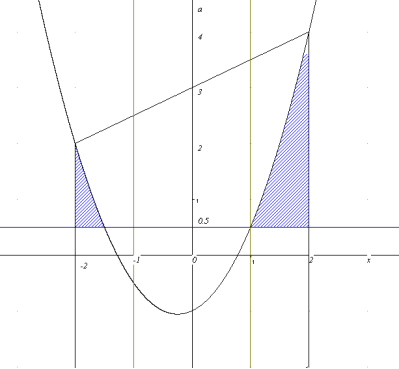
На наступному графіку відмічена множина точок розв’язків даної системи, що задовольняють умову ![]() .
.
![]()
![]()
![]()
![]()
![]()
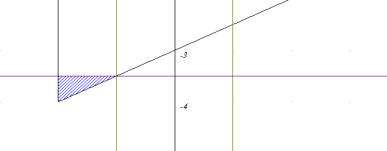
Знайдемо при яких знаннях а виконується умова ![]() .
.
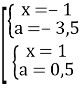
Отже система має тільки розв’язки, що задовольняють умову ![]() при
при ![]()
6. Знайдемо, при яких значеннях параметра а множина розв’язків системи містить не більше одного цілого числа.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Система має в множині розв’язків тільки одне ціле число х=-2 при ![]() або х=2 при
або х=2 при ![]()
Отже система має множину розв’язків, що містить не більше одного цілого числа при
![]()


про публікацію авторської розробки
Додати розробку
