Урок з алгебри "Сума перших n членів арифметичної прогресії"

Про матеріал

Тема: Сума перших n членів арифметичної прогресії.

Мета:

- вивести формулу для обчислення суми n перших членів арифметичної прогресії, сформувати вміння застосовувати цю формулу до розв'язування задач;

- розвивати логічне мислення, увагу, пам'ять, обчислювальні навички;

- виховувати інтерес до предмета, показати зв'язок математики з життям.

Тип уроку: урок засвоєння нових знань, вмінь і навичок.

Перегляд файлу

Урок № 43 Дата 12.01.18

Клас: 9

Тема: Сума перших n членів арифметичної прогресії.

Мета:

 вивести формулу для обчислення суми n перших членів арифметичної прогресії, сформувати вміння застосовувати цю формулу до розв’язування задач;

 розвивати логічне мислення, увагу, пам'ять, обчислювальні навички;

 виховувати інтерес до предмета, показати зв’язок математики з життям.

Тип уроку: урок засвоєння нових знань, вмінь і навичок.

Обладнання та наочність: підручник, конспект, картки, роздатковий матеріал, проектор, ноутбук.

Хід уроку

І. Організаційний етап. Рефлексія.

Розпочалося вже століття ХХ І

То, може, люди будуть прагнуть знати менше?

Здається вивчені вже космос і моря,

Зірок будова і уся Земля.

Чи варто зайвий раз ризикувати

Заради того, щоб нове щось узнати?

Такі питання математиків дратують,

Вони сьогодні, як завжди,

Досліджують, розв’язують, рахують.

І не бояться ні труднощів, ні перешкод, ані тенет,

Бо точно знають, що “Прогресіо” – це рух впред”

Дійсно слово «прогрес» перекладається з латинського як «рух вперед» або «крок вперед», тому я хочу допомогти вам зробити крок вперед до нових знань. Бажаю успіхів сьогодні на уроці! Тема уроку: «Сума n перших членів арифметичної прогресії.» Щоб досягнення успіху, нам потрібно сформулювати завдання та мету.

ІІ. Перевірка домашнього завдання. Актуалізація знань.

Учні перевіряють правильність виконання домашнього завдання з відповідями на картках і за потреби роблять виправлення.

№ 16.25(1); № 16.18; № 16.9.

№16.9

а₈ = 3, а₉ = -12

d = а₉- а₈ = (-12) – 3 = -15

№16.18

х₈ = 58, х₁₅ = 16

х₈ = х₁ + 7 d, х₁₅ = х₁ + 14d

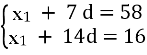
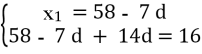
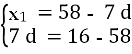
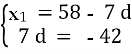
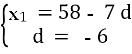
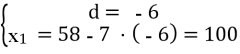
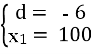
№16.25 (1)

а₃ + а₇ = 30, а₆ + а₁₆ = 60,

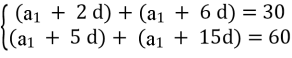
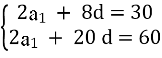
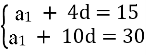
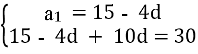
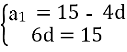
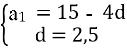
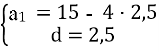
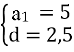
Б) Усно. Інтерактивна вправа «Лабірінт відповідності»

1. Арифметична прогресія	А.
2. Приклади арифметичних прогресій	Б. Прогресія, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додано одне й те саме число
3. Формула n-го члена арифметичної прогресії	В.
4. Властивість n-го члена арифметичної прогресії	Г.1) послідовність натуральних чисел; 2) 4, 7, 10, 13, 16… 3) 100, 95, 90, 85 …

В) Індивідуальна робота учнів з картками («слабі» учні)

Г) Повідомлення учнів

«Магічний квадрат»

Послідовність чисел 3, 5, 7, 9, 11, 13, 15,17, 19 являє собою арифметичну прогресію. Крім того, дана зграйка чисел приваблива здатністю розміститися в дев'яти клітках квадрата 3х3 так, що утворюється магічний квадрат з константою, рівної 33. Справа в тому, що з кожних дев'яти послідовних членів будь-якої арифметичної прогресії натуральних чисел можна скласти магічний квадрат. Такий магічний квадрат зображено на гравюрі німецького художника А. Дюрера «Меланхолія»

«Історія арифметичної прогресії»

Термін “прогресія” був уведений римським автором Боэцием ще в IV с. н.е. Від латинського слова progressio – “рух уперед”. Перші спогади про арифметичну прогресію були ще у прадавних народів. У клинописних вавилонських табличках і єгипетських папірусах зустрічаються задачі на прогресії та вказівки як їх розв’язувати. Найдавніші задачі на прогресії зустрічаються у єгипетському папірусі Ахмеса Ринда. Значна кількість задач на прогресії містяться у пам’ятці математичної літератури початку XVIII століття «Арифметиці»

Магницького Л.П. Перші задачі на прогресії які дійшли до нас, пов'язані з потребами господарства і суспільної практики, як наприклад, розподіл харчів, ділення спадщини і т.д.

ІІІ. Мотивація навчання

Прогресії є відображенням світу, що нас оточує. Застосовуються в таких науках

як фізика, геометрія, біологія, хімія, економіка та навіть у літературі. Широко використовують формули арифметичної прогресії в будівництві. Щоб виконати розрахунки потрібно знати формули суми членів арифметичної прогресії.

ІV. Вивчення нового матеріалу.

Нехай задано скінчену арифметичну прогресію а:

Розповідь учителя про Карла Гауса

Якось учитель дав учням досить складне завдання з арифметики: відшукати суму ста натуральних послідовних чисел. Учитель вважав, що учні досить довго шукатимуть відповідь. Але через кілька хвилин Карл розв'язав задачу. Коли вчитель проглянув розв'язання, то побачив, що малий Гаус винайшов спосіб скороченого знаходження суми членів арифметичної прогресії. Видатний німецький математик Карл Гаус (1777 – 1855) розв’язав цю задачу у віці 5 років.

Як він це зробив?

1+2+3+4+5+…+95+96+97+98+99+100=(1+100)+(2+99)+(3+98)+…=101*50=5050

Одже або

V. Засвоєння нових знань і вмінь.

Усно: Приклад 1 с.168

Письмово: 1) №17.4 ; ( додаткове завдання №17.10)

2) Піраміди фараонів

Будуючи піраміди для фараонів, єгиптяни в кожному наступному ряду плит встановлювали на одну плиту менше, ніж в попередньому. На самому верху стіни підноситься одна плита. Скільки всього плит знадобиться тільки для однієї стіни піраміди, якщо плити стоять в 60 рядів?

3) Історична задача з

«Арифметики» Магницького Л.П.

Купець мав 14 срібних чарок, причому вага чарок зростає за арифметичною прогресією з різницею 4. Остання чарка важить 59 лотів. Визначте скільки важать усі чарки. ( Лот – стародавня міра ваги, яка дорівнює 12,8 г)