Урок 9 клас "Арифметична прогресія"

Арифметическая прогрессия

Тип урока: урок изучения нового материала.

Цель урока: Формирование понятия арифметической прогрессии как одного из видов последовательностей, вывод формулы n-го члена, знакомство с характеристическим свойством членов арифметической прогрессии.

Актуализация знаний, устная работа.

1. Что мы называем последовательностью?
2. Какие способы задания последовательности вы знаете?
3. О последовательности (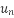) известно, что 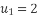, 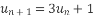. Как называется такой способ задания последовательности? Найдите первые четыре члена этой последовательности.
4. О последовательности (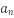) известно, что 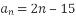. Как называется такой способ задания последовательности? Найдите n, если?
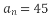5. Последовательность (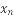) задана формулой: 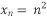. Какой номер имеет член этой последовательности, если он равен 169? 256? 121? Являются ли членами этой последовательности числа 54? 81? 192?

Мотивация

Продолжительность Земного года равна 365 суток, а точнее 365 ¼ суток. Поэтому каждые 4 года набегают одни сутки. Для учета этих суток каждый четвертый год больше на одни сутки. Запишем последовательность високосных годов, начиная с 2000 года

2000, 2004, 2008,2012, 2016, 2020, …

Как мы получили такую последовательность? (каждый последующий член равен предыдущему, к которому прибавили одно и то же число)

Мы получили особый вид последовательности. Наша задача: изучить такие последовательности, дать им название, определение, изучить их свойства.

III. Изучение нового материала.

Прогрессия - последовательность величин, каждая следующая из которых находится в некоей, общей для всей прогрессии, зависимости от предыдущей. Термин ныне во многом устарел и встречается только в сочетаниях "арифметическая прогрессия" и "геометрическая прогрессия".

Термин "прогрессия" имеет латинское происхождение (progression, что означает "движение вперед") и был введен римским автором Боэцием (VI в.). Этим термином в математике прежде именовали всякую последовательность чисел, построенную по такому закону, который позволяет неограниченно продолжать эту последовательность в одном направлении. В настоящее время термин "прогрессия" в первоначально широком смысле не употребляется. Два важных частных вида прогрессий - арифметическая и геометрическая - сохранили свои названия.

Рассмотрим последовательности чисел:

• 3, 7, 11, 15, 19, …
• 10, 6, 2, -2, -6, …
• 8, 8, 8, 8, 8, …

Чему равен третий член первой последовательности? Последующий член? Предыдущий член? Чему равна разность между вторым и первым членами? Третьим и вторым членами? Четвертым и третьим?

Если последовательность построена по одному закону, сделайте вывод, какой будет разность между шестым и пятым членами первой последовательности? Между седьмым и шестым?

Назовите два последующих члена каждой последовательности. Почему Вы так считаете?

(Ответы учеников)

Каким общим свойством обладают эти последовательности? Сформулируйте это свойство.

(Ответы учеников)

Числовые последовательности, обладающие этим свойством, называются арифметическими прогрессиями. Предложить учащимся самим попробовать сформулировать определение.

Определение арифметической прогрессии: арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом:

() - арифметическая прогрессия, если , где d - некоторое число.

Число d, показывающее, на сколько следующий член последовательности отличается от предыдущего, называется разностью прогрессии: .

Давайте еще раз посмотрим на последовательности и поговорим о различиях. Какие особенности есть у каждой последовательности и с чем они связаны?

Если в арифметической прогрессии разность положительна (d ˃ 0), то прогрессия является возрастающей: 3, 7, 11, 15, 19, … (d = 4)

Если в арифметической прогрессии разность отрицательна (d ˂ 0 ) , то прогрессия является убывающей: 10, 6, 2, -2, -6, … (d = - 4 )

В случае, если разность равна нулю (d = 0) и все члены прогрессии равны одному и тому же числу, последовательность называется стационарной: 8, 8, 8, 8, …

Как задать арифметическую прогрессию? Рассмотрим следующую задачу.

Задача. На складе 1 числа было 50 тонн угля. Каждый день в течение месяца на склад приходит машина с 3 тоннами угля. Сколько угля будет на складе 30 числа, если в течение этого времени уголь со склада не расходовался.

Если выписать количество угля, находящегося на складе каждого числа, получим арифметическую прогрессию. Как решить эту задачу? Неужели придется просчитывать количество угля в каждый из дней месяца? Можно ли как-то обойтись без этого? Замечаем, что до 30 числа на склад придет 29 машин с углем. Таким образом, 30 числа на складе будет 50+3 ◦ 29 = 137 тонн угля.

Таким образом, зная только первый член арифметической прогрессии и разность, мы можем найти любой член последовательности. Всегда ли это так?

Проанализируем, как зависит каждый член последовательности от первого члена и разности:

:::::::::::::

Таким образом, мы получили формулу n-ого члена арифметической прогрессии.

Рассмотрим следующую задачу:

В арифметической прогрессии четные члены оказались затерты: 3, … 7, …, 11: Можно ли восстановить утраченные числа?

Учащиеся, скорее всего, сначала вычислят разность прогрессии, а затем будут находить неизвестные члены прогрессии. Тогда можно предложить им найти зависимость между неизвестным членом последовательности, предыдущим и последующим.

Решение: Воспользуемся тем, что в арифметической прогрессии разность между соседними членами постоянна. Пусть - искомый член последовательности. Тогда 

.

Замечание. Данное свойство арифметической прогрессии является ее характеристическим свойством. Это означает, что в любой арифметической прогрессии каждый член, начиная со второго равен среднему арифметическому предыдущего и последующего ( . И, наоборот, любая последовательность, в которой каждый член, начиная со второго равен среднему арифметическому предыдущего и последующего, является арифметической прогрессией.

Рефлексия – лесенка успеха

ІІІ Решение задач.

Пример: №16.8 (устно)

Чему равна разность арифметической прогрессии (), если  

Применение формулы n – го члена арифметической прогрессии.

Пример: №16.5

Первый член арифметической прогрессии  ( равен 4, а разность равна  0,4. Найти .

Применение формулы n – го члена арифметической прогрессии для нахождения ее первого члена.

Пример: №16.11

Найдите первый член арифметической прогрессии (), если а разность  d = 0,5.

Применение формулы n – го члена для нахождения разности арифметической прогрессии

Пример: № 16.10

Найдите разность арифметической прогрессии(), если  

Практическое применение.

Учащиеся разбиваются на три групп.  Им предлагается решить задачи.

Первая группа:

Задача. На протяжении семи дней перед математической олимпиадой ученик решал задачи. В первый день он решил 7 задач, а в каждый последующий – на 2 задачи больше, чем в предыдущий. Сколько задач решил ученик в седьмой день.

Вторая группа:

Задача. В течение месяца радиостанция проводила ежедневный конкурс среди своих слушателей. Каждый последующий день призовой фонд был меньше на 200 гривен. На одиннадцатый день призовой фонд составлял 4000 гривен. Какой призовой фонд был в первый день конкурса?

Третья группа:

Задача. В течение первого года с момента регистрации туристическая фирма открыла 8 своих филиалов. В конце седьмого года существования туристической фирмы было открыто 32 филиала. Сколько филиалов в год открывала туристическая фирма?

I V Подведение итога урока

Рефлексия

Что узнали на уроке?

Рефлексия – лесенка успеха

Как усвояли материал?

Закончить наш урок я хочу словами великого учёного Фалеса:

"Что есть больше всего на свете? - Пространство.

Что быстрее всего на свете? - Ум.

Что мудрее всего? - Время.

Что приятнее всего? - Достичь желанного".