РОЗВ’ЯЗУВАННЯ ФІЗИЧНИХ ЗАДАЧ для 9 класу З ВИКОРИСТАННЯМ ЗАСОБІВ МУЛЬТИМЕДІА

Ю.Ф. Плаксюк

 

 

 

 

 

 

 

РОЗВ’ЯЗУВАННЯ ФІЗИЧНИХ ЗАДАЧ З ВИКОРИСТАННЯМ ЗАСОБІВ МУЛЬТИМЕДІА

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рокитне

2021

 

 

Автор-упорядник: Плаксюк Юлія Федорівна, вчитель фізики.

                                

 

РОЗВ’ЯЗУВАННЯ ФІЗИЧНИХ ЗАДАЧ для 9 класу З ВИКОРИСТАННЯМ ЗАСОБІВ МУЛЬТИМЕДІА. -Рокитне: 2021 –  91  с.

 

 

Рецензент:  –  Радіон Людмила Ростиславівна

 

 

 

В посібнику викладені основні методики розв’язування задач з усіх розділів фізики згідно шкільної програми за 9 клас середньої школи. В ньому надаються базові фізичні формули та типові приклади задач з детальними поясненнями, малюнками та схемами. Посібник містить достатню кількість задач до самостійної роботи.

Викладений матеріал посібника допоможе урізноманітнити урок фізики через впровадження ІКТ в освітній процес, зокрема на уроці фізики. Даний посібник дозволить учителю підвищити інтерес учнів до вивчення фізики, забезпечити міцність засвоєння знань школярів та вміння застосовувати ці знання у практичній діяльності, допоможе розвивати аналітичне та логічне мислення. Матеріали, вміщені у посібнику, сприятимуть творчому зростанню вчителя фізики та активності учнів на уроках, допоможуть зробити процес навчання з фізики цікавим, різноманітним, ефективним, демократичним.

 Дані матеріали допоможуть вчителю надавати практичні рекомендації щодо застосування комп’ютерної техніки та застосовування прийомів та методів, що забезпечують формування ключових компетентностей учнів у процесі навчання.

  Видання рекомендоване педагогічним працівникам загально-освітніх навчальних закладів.

 

 

 

Рекомендовано методичною радою

Рокитнівського ліцею №2

Рівненської області

Протокол №3 від 05 лютого 2021 року

 

Зміст

 

 

Передмова………………...………………………………………………..…4

І. Магнетизм

Методика розв`язування задач………………………………………………7

1.      Магнітне поле. Дослід Ерстеда ………………………………..………..9
2.      Електромагнітна індукція. ………………………………………..……12

ІІ. Оптика

Методика розв`язування задач……………………………………………...19

1.      Швидкість поширення світла.

 Закони відбивання світла……………………………….….…………….....22

2.      Заломлення світла……………...………...……………………………...28
3.      Лінзи. Оптичні системи……………….…..…………………….……....35

ІІІ. Механічні та електромагнітні хвилі

Методика розв`язування задач……………………………………………...42

1.      Механічні коливання та хвилі………………………………………….43
2.      Електромагнітні коливання і хвилі…………………………………….48

VI. Фізика атома та атомного ядра. Фізичні основи атомної енергетики

Методика розв`язування задач……………………………………………...52

1.      Радіоактивність. Період піврозпаду радіонукліда…………………….56
2.      Термоядерні реакції……………………………………………………..59

V. Механіка

Методика розв`язування задач………………………………………………63

1.      Прямолінійний рівноприскорений рух…………………………………65
2.      Закони Ньютона………………………………………………………….69
3.      Закон Всесвітнього тяжіння.Штучні супутники Землі.
4.      Перша космічна швидкість……………………………………………...74
5.      Рух тіла під дією сил…………………………………………………….78

Додаткові матеріали

Додаток : Фізичні сталі……………………………………………….……...88

Використані джерела…………….……………………….………………...90

 

 

 

 

 

 

 

 

 

 

Передмова

 

   Знання фізики - це насамперед розуміння фізичних явищ, законів і величин, що їх характеризують. Тому розв'язування учнями задач під час вивчення фізики має надзвичайно велике значення. Відомо, що чим більше учні розв'язують задач, тим швидше вони поглиблюють і розширюють свої знання про фізичні величини, явища, закони, теорії і міцніше засвоюють навчальний матеріал.

Навчання - це не лише запам'ятовування формулювань законів та їх математичних формул, а й свідоме розуміння учнями фізичної суті цих законів, уміння використовувати їх практично.

Ефективність вивчення курсу фізики, очевидно, буде найбільшою лише тоді, коли учні виявлятимуть максимум ініціативи й самостійності до будь - якого виду роботи, з вивчення курсу фізики і особливо під час розв'язування фізичних задач.

Щоб забезпечити самостійність та уникнути формалізму під час розв'язування задач, треба частіше впроваджувати індивідуальні завдання як безпосередньо на уроці, так і вдома.

Розв'язування задач є однією з найважливіших складових частин у системі навчання фізики. Задачі з фізики можна ефективно використовувати на різних етапах вивчення матеріалу, а саме:

•      Для постановки проблеми;
•      Під час вивчення нового матеріалу;
•      Для формування практичних умінь і навичок та їх використання в майбутній професії;
•      Для перевірки якості засвоєння матеріалу;
•      Під час повторення, закріплення й узагальнення матеріалу;

Для розвитку творчих здібностей учнів.

У курсі фізики підбирається система задач так, щоб їх розв'язування допомогло формуванню єдиної цілісної науково-фізичної картини (як окремих розділів, так і загальної у цілому). У цю систему обов'язково входять як навчальні й узагальнюючі задачі, так і задачі для самостійного розв'язування та для контролю знань.

Логіка здобування нових знань у фізиці має особливу структуру:

•      Узагальнення сукупності експериментальних знань;
•      Формування на їх основі фізичної моделі;
•      Планування експерименту дня підтвердження результатів цієї моделі та встановлення меж її застосування або повна відмова від неї у разі її нествердження.

Складаючи систему фізичних задач, слід ураховувати структурну особливість фізичної науки і саму структуру предмета навчання. Ефективність навчання розв'язування задач визначається, в першу чергу, тими завданнями, які ставляться перед розв'язуванням кожної задачі в системі всієї навчальної роботи. Виходячи зі сказаного вище і слід складати систему задач.

Підібрані задачі мають відповідати таким дидактичним вимогам, основою яких є поступове ускладнення зв'язків між величинами й поняттями, що характеризують процес або явище, описуване в задачі.

Під час вивчення окремого питання спочатку розв'язують якісні задачі, потім - розрахункові, експериментальні, графічні, поступово збільшують кількість зв'язків між величинами і поняттями. На заключному етапі розв'язують комбіновані задачі, які включають у себе значне коло питань, що вимагають знань раніше вивченого матеріалу. Комбіновані задачі допомагають встановити місце матеріалу, що розглядається, у системі фізичних знань.

Методика навчання розв'язуванню задач припускає певну загальну послідовність етапів і алгоритм розв'язування задач з конкретної теми.

Загальна послідовність етапів розв'язування задач. (один з можливих варіантів).

1.      Читання умови задачі з поясненням термінів.
2.      Пояснення фізичної суті задачі.
3.      Короткий запис умови з переводом у єдину систему вимірювання фізичних величин.
4.      Виконання малюнка відповідно до фізичної моделі задачі.
5.      Складання плану розв'язування.
6.      Складання системи рівнянь (тобто математичної моделі задачі), розв'язуючи яку, знайдемо відповідь на запитання задачі.
7.      Розв'язування задачі в загальному вигляді. Аналіз одержаної формули.
8.      Знаходження числового значення шуканої величини та її розмірності.
9.      Дослідження та аналіз відповіді.

Така послідовність дає змогу привчити учнів до певного порядку під час аналізу та розв'язування задачі. Крім того, слід зазначити, що така послідовність полегшує завдання вчителя навчити учня розв'язуванню фізичних задач. Додержуючи загальної послідовності, учні швидше оволодівають навичками й уміннями розв'язування задач з даної теми. А якщо таку послідовність застосовувати для розв'язування аналогічних задач з різних тем, то досягається досить глибоке засвоєння нового поняття, нового закону, способу розв'язування.

 Одним із пріоритетних напрямів розвитку фізики як шкільного предмету є впровадження освітніх інновацій та інформаційних технологій для підтримання навчально-виховного процесу. Відповідно до нормативно-правової бази викладання курсу фізики впровадження інформаційно-комп’ютерної техніки забезпечує доступність та ефективність освіти, підготовку молодого покоління до життєдіяльності в інформаційному суспільстві, істотне розширення пізнавальних можливостей людини. Тому надзвичайно важливим напрямом модернізації освіти є її інформатизація. Основна мета цього посібника – збагатити урок фізики через впровадження ІКТ у поєднанні з інтеграційними аспектами викладання навчального матеріалу, показати можливості застосування ІКТ на різних етапах уроку, продемонструвати спектр наявних педагогічних програмних засобів навчального призначення для підтримання навчально-виховного процесу фізики, надати практичні рекомендації щодо застосування ІКТ у ході викладання фізики в загальноосвітній школі, а саме при розв’язуванні задач, адже без них учень не може повною мірою засвоїти теоретичний матеріал, закони та формули. Учні, зазвичай, стикаються з певними труднощами при розв’язуванні задач, а саме, коли переходять до обчислень. Тому, мета цього посібника полягає у допомозі учням орієнтуватись в певних алгоритмах при розв’язуванні фізичних задач, наочно побачити, як відбувається певний процес чи явище, описане в умові задачі.

У посібнику викладено послідовно основні теоретичні відомості по всіх темах за 9 клас середньої школи.  Весь матеріал поділено на 5 розділів. Кожен розділ містить в собі по кілька змістових модулів, в яких міститься по 4-9 задач кожного рівня складності, 3-7 задач для самостійного розв’язування. Всі задачі виконані з детальним поясненням програмового матеріалу та мають чіткий алгоритм розв’язування. Всього в посібнику міститься  69  задач з розв’язками та     68 задач самостійного виконання. В сумі 137 задач. У посібнику розглянуто доцільність та можливості використання засобів ІКТ під час розв’язування задач з фізики, зокрема використано пакети програм Microsoft Office PowerPoint, Microsoft Office Excel, Power Point, система Mathcad.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

І. Магнетизм

Методика розвязування задач на «Магнітні явища»

Поняття магнітного поля (МП) вводять на основі досліду Ерстеда. Тобто одразу вводять достатньо складне загальне поняття МП як такого, що існує навколо провідників зі струмом, а значить, і навколо рухомих електрично заряджених частинок. При цьому не враховують, що магнітна взаємодія у свідомості учнів асоціюється спочатку не зі струмом, а через взаємодію постійних магнітів, яка за навчальною програмою вивчається в другу чергу. • При вивченні електричних явищ існує ускладнення в розкритті магнітної дії електричного струму ще до вивчення поняття МП. Ще в більшій мірі це стосується введення одиниці сили струму 1 А: переважна більшість учнів на цьому етапі не розуміють, чому між провідниками зі струмом існує саме магнітна взаємодія, оскільки магнітні явища вивчають тільки після електричних.

Ми досягаємо поставленої мети завдяки побудові змісту, структури й методики навчання електромагнетизму в основній школі на засадах генералізації навчального матеріалу на основі 1) понять електромагнітної взаємодії та електромагнітного поля, а також елементів електронної теорії та 2) явищного (феноменологічного) підходу. Відповідно до цього весь навчальний матеріал з електромагнетизму об’єднуємо під спільним заголовком «Електромагнітні явища. Електромагнітне поле».

Покроково обґрунтовуємо: навколо Землі та постійних магнітів існує МП; магнітна взаємодія здійснюється завдяки наявності магнітного поля; МП є тим «посередником», завдяки якому здійснюється магнітна взаємодія на відстані. Переконуємо учнів у реальності існування МП та демонструємо, що наявність МП легко виявити за його орієнтаційною дією на магнітну стрілку. Посилаємось на відомий у фізиці експериментальний факт, що магнітна стрілка орієнтується певним чином навколо рухомих електрично заряджених частинок. Допомагаємо учням зрозуміти, що навколо рухомих електрично заряджених частинок (тіл) існує МП. Тобто, ми одразу надаємо узагальнені відомості: навколо нерухомих електрично заряджених частинок (тіл) існує електричне поле, а навколо рухомих – як електричне поле, так і МП. Надаємо початкові відомості про електромагнітну взаємодію, яка передається зі швидкістю 3·108 м/с у вакуумі, та електромагнітне поле , у тому числі підкреслюємо, що МП є одним з проявів електромагнітного поля. Переконуємо учнів на конкретних прикладах у тому, що оскільки електромагнітне (електричне, магнітне) поле здатне виконати роботу, то електромагнітне (електричне, магнітне) поле має певну енергію. Згадуємо про існування такого виду матерії як речовина та обґрунтовуємо, що електромагнітне поле є видом матерії (не менш реальним, ніж речовина), що існує два види матерії – речовина і поле.

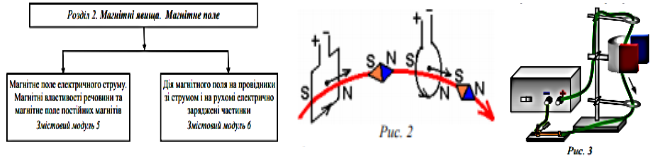
У розділі 2 «Магнітні явища. Магнітне поле» продовжуємо вивчати магнітні явища і поглиблюємо уявлення про магнітну взаємодію та МП в межах двох змістових модулів, відображених на рис. 1 . Структура і наповнення змістового модуля 5 зумовлені наступним: 1) розвиваємо уявлення про магнітні явища, магнітну взаємодію, МП, саме як прояви електромагнітної взаємодії та електромагнітного поля; 2) детально вивчаємо картини ліній МП прямого провідника, кільця та соленоїда зі струмом з відповідними мнемонічними правилами, що сприяє розвитку дивергентного мислення; 3) поєднуємо вивчення магнітних властивостей речовини на основі електронної теорії з розширенням уявлень про «джерела» МП на основі розкриття природи МП постійних магнітів. Навчальний матеріал розкриваємо в такій послідовності.

 1. МП провідників зі струмом.

1.1. Лінії МП та їх напрям. МП вивчаємо не як відокремлений самодостатній вид поля, а як один з проявів електромагнітного поля. Для посилення уявлення учнів про МП вводимо поняття ліній МП та їх напряму. Лінії, вздовж яких розташовуються в МП осі маленьких магнітних стрілок або залізних ошурок, називають лініями МП. Напрям, який вказують північні полюси магнітних стрілок в кожній точці поля, прийняли за напрям ліній МП. Зазначене поняття ліній МП та їх напряму не суперечить науково виваженому поняттю ліній індукції МП, котре вивчають в старших класах. Одразу підкреслюємо, що реально існує тільки МП, а поняття ліній МП вводять для візуалізації наших уявлень про поле.

1.2. МП прямого провідника зі струмом. На основі демонстраційного експерименту (спостерігаємо за розташуванням маленьких магнітних стрілок і залізних ошурок навколо прямого провідника зі струмом при двох напрямах струму) підводимо учнів до висновку, що лінії МП прямого провідника зі струмом являють собою співвісні концентричні кола, центри яких співпадають з віссю провідника. Формулюємо правило свердлика та правило правої руки. Відмітимо, що для частини учнів, котрі погано уявляють собі закручування гвинта, більш доступним є правило правої руки.

1.3. МП соленоїда. Спостерігаємо на досліді та обґрунтовуємо теоретично картину ліній МП соленоїда. На основі орієнтації магнітних стрілок уводимо північний N і південний S полюси соленоїда та кільця зі струмом. Передбачаємо теоретично та перевіряємо на досліді, що соленоїди (кільця) зі струмом, як і магніти, притягуються до інших соленоїдів (кілець) зі струмом чи магнітів різнойменними полюсами і відштовхуються від них однойменними полюсами. Демонструємо, що МП виявляє орієнтаційну дію на рамку зі струмом чи маленький соленоїд і за їх допомогою можна вивчати картину МП (рис. 2).

1.4 Три основні типи магнетиків. Посилаємось на досліди і розкриваємо, що за магнітними властивостями речовину можна розділити на три основних типи магнетиків – феромагнетики, парамагнетики, діамагнетики; наводимо їх приклади. Розкриваємо природу магнетиків. Діамагнетики – це речовини, у яких результуюче МП кожного атома (молекули) рівне нулю; діамагнетики не мають власного МП. Парамагнетики – це речовини, кожен атом (молекула) яких має своє МП, але магнітна взаємодія між атомами (молекулами) слабка і внаслідок хаотичного теплового руху МП різних атомів (молекул) орієнтуються хаотично, тому результуюче МП парамагнетика дорівнює нулю. Феромагнетики – це речовини, атоми (молекули) яких мають власні МП, котрі внаслідок сильної магнітної взаємодії між різними атомами (молекулами) вилаштовуються в одному напрямі в межах доменів.

2. Дія магнітного поля на провідники зі струмом.

2.1. Сила Ампера. Правило лівої руки. Спочатку демонструємо дію магнітного поля на вертикальний провідник зі струмом (рис. 3), у якому чітко видно на яку саме ділянку провідника діє МП. Формулюємо правило лівої руки, використовуючи поняття напряму ліній МП. Демонструємо, що сила Ампера зростає при збільшенні сили струму в провідникові та посиленні МП. Зазначаємо про зростання сили Ампера зі збільшенням довжини провідника, що знаходиться в МП. Ми підкреслюємо, що сила Ампера найбільша, коли провідник розташований перпендикулярно до ліній МП, а для провідника, розташованого вздовж ліній МП, сила Ампера дорівнює нулю.

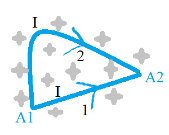
2.2. Взаємодія паралельних провідників зі струмом. На основі правила лівої руки розкриваємо (рис. 4), що між провідниками зі струмом існує саме магнітна взаємодія, оскільки МП одного провідника зі струмом діє на інший провідник зі струмом. Обґрунтовуємо введення одиниці сили струму 1 А.

 

 

 

 

 

 

 

 

 

 

 

 

1. Магнітне поле. Дослід Ерстеда

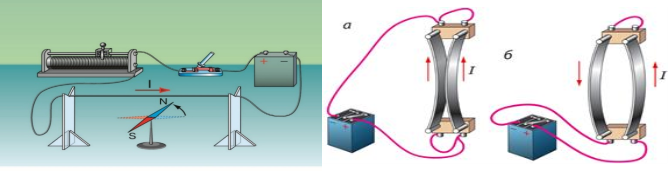
15 лютого 1820 р. данський фізик Г. Ерстед демонстрував студентам дослід із нагріванням провідника електричним струмом. У ході досліду вчений помітив, що під час проходження струму магнітна стрілка, розташована поблизу провідника, відхилялася від напрямку «північ — південь», встановлюючись перпендикулярно до провідника. Як тільки струм припинявся, стрілка знову поверталася в початкове положення. Так було з’ясовано, що електричний струм здійснює певну магнітну дію:

• Якщо в двох паралельних провідниках течуть струми одного напрямку, провідники притягуються (а).
• Якщо протилежних напрямків — провідники відштовхуються (б).

Задачі

Середній рівень

1.      Як можна дістати металеву скріпку з посудини зводою, не опускаючи в неї ніяких предметів? ( Поставити над водою магніт).  

 

 

 

 

Достатній рівень

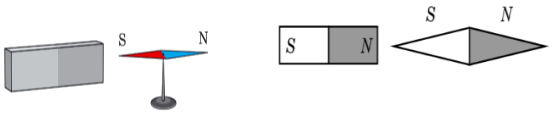
2.      Магнітну стрілку поставили біля штабового магніту. Як визначити полюси? Відповідь: (Врахувати властивість полюсів магнітів, то північний полюс стрілки притягнеться до півненного полюсу магніта).

 

 

 

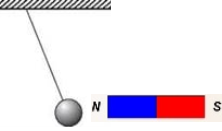
3.      Магніт північним полюсом підносять до залізної кульки, яка підвішена на нитку. Кулька притягнеться чи відштовхнеться від магніту?

Відповідь: (Під дією магнітного поля магніту кулька на ближчому боці до магніта створить протилежний полюс, а в нашому випадку – південний, і притягнеться до магніту). 

 

 

 

 

 

Високий рівень

4.      Є дві сталеві пластинки однакові за розміром та формою, одну з яких намагнітили. Як визначити, котру саме пластину намагнітили, не використовуючи жодних додаткових приладів?

Відповідь: (По черзі підносимо кінець одної пластини до середини іншої. Де відбудеться притягання тої пластини, яку підносим, то та пластина і намагнічена).

 

 

 

 

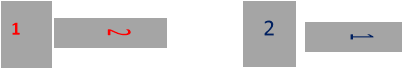
Задачі для самостійного виконання:

1.      Яким полюсом має повернутися магнітна стрілка до учня? Чи зміниться положення стрілки, якщо її розташувати над провідником.

 

 

 

 

 

 

 

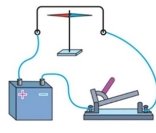
2. Як поведе себе котушка, якщо до неї піднести постійний штабовий магніт?

 

 

 

 

 

 

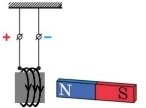
3. Чим пояснити, що магнітна стрілка встановлюється на даному місці Землі в певному напрямі?

4.  Дві голки підвісили на нитці. Коли до них наблизили магніт, вони почали

    відштовхуватись одна від одної. Чому?

6. Намалювати, як зберігаються два штабові магніти в коробочці. Проставити полюси.
7. Чому  постійний магніт може втримати ряд з декількох залізних предметів?

 

 

 

 

 

 

3. Електромагнітна індукція.

 

Електромагні́тна інду́кція — явище створення в просторі вихрового електричного поля змінним магнітним потоком. Одним із наслідків електромагнітної індукції є зв'язок між змінними електричним та магнітними полями в електромагнітній хвилі, інший наслідок, практично важливий для генерації електричного струму, — виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачі

Достатній рівень

1. Магнітна стрілка встановилася в магнітному полі котушки зі струмом так, як показано на рисунку. Визначте полюси джерела струму.

Відповідь: Щоб магнітна стрілка притягувалася до котушки Sполюсом потрібно, щоб у котушки справа був N полюс. Знаючи розміщення полюсів котушки використаємо правило правої руки (або свердлика), щоб визначити напрямок струму. Справа «+», зліва «-».

 

 

 

 

 

 

 

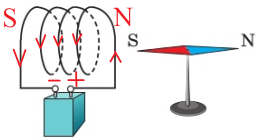
2.  На рисунку зображено рамку, що повертається в магнітному полі постійного магніту. Визначте полюси джерела струму, до якого підключено рамку.

 

 

 

 

 

 

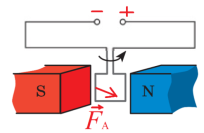
Відповідь: Напрямки струму, магнітних ліній та сили Ампера, які повертають рамку, пов’язані правилом лівої руки .Для даної задачі ліву руку розташуємо так, щоб лінії магнітного поля входили в долоню, а відігнутий на 90° великий палець вказував напрямок сили Ампера так щоб рамка оберталася у вказаному напрямку, то чотири витягнуті пальці вкажуть напрямок струму в провіднику.

 

3. Описати рух дротяної рамки зі струмом у магнітному полі Землі та її рух у полі стального магніту, якщо вона вільно підвішена.

Відповідь: Рамка, прямокутної форми має дві паралельні сторони, на які в однорідному магнітному полі діють сили Ампера, рівні за модулем та протилежно напрямлені. На мал.1 сили F1 I F2 повертають рамку так, що її площина перпендикулярна до вектора магнітної індукції B. У положенні рівноваги струм в рамці пов'язаний з магнітною індукцією В за правилом свердлика, а сили F1 I F2 намагають її розвести в різні сторонони, мал.2. Тому, якщо говорити про магнітне поле Землі, то магнітне поле робить лише направляючу дію на рамку. Якщо ж говорити про неоднорідне поле магніту, то сили F1 I F2 мають рівнодійну, яка недорівнює нулю, при цьому рамка обертається та тягнеться в область більш сильнішого поля, притягуючись до магніту як на мал.3.

 

 

 

 

 В

F1   F2 F2

    F2 F1 F1

Мал.1 мал.2  мал.3

 

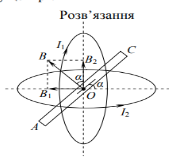
4.           Два обручі розташовані так, як показано на малюнку. По них течуть однакові струми. Знайти напрями векторів магнітної індукції В у спільному центрі двох обручів?

                                                                          2

                                                  1

 

Відповідь: На малюнку обруч показано у вигляді кола. За правилом свердлика струм І2 в центрі О горизонтального обруча створює індукцію В2, а струм І1 в центрі О вертикального обруча – індукцію В1. Вектори В2 і В1 взаємно перпендикулярні і рівні за модулем, тому що І1=І2. Результуючий вектор В утворює як з вертикальною площиною, так і з горизонтальною кут  =45°. Рамка з струмом АС, що знаходиться в центрі О займе таке положення, що її площина утворить з вектором В кут рівний 2  , а з горизонтальною площиною – кут α.

 

 

 

 

 

Середній рівень

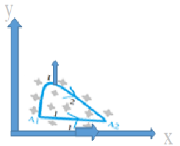5. Два провідники  лежать в одній площині, яка перпендикулярна до однорідного магнітного поля, як показано на малюнку. Довести, що на провідники діють однакові сили Ампера за модулем та напрямом, якщо в провідниках течуть однакові струми?

 

 

 

Відповідь: Спрямовуємо перший провідник вздовж осі ОХ так, як показано на малюнку. То сила Ампера F1, що діє на цей провідник піде вздовж осі ОУ і буде рівна І*В (струм помножити на магнітну індукцію).Щоб обчислити силу Ампера F2, що діє на другий провідник, уявно ділимо його на декілька частин і розглядаємо силу одної уявної ділянки. Вважаючи, що її довжина l , отримаємо формулярно: , а її проекції по осях координат матимуть такий формулярний вид:              

З формул видно, що модулі F1=F2, тобто вони чисельно рівні, то для замкненого провідника F=0.     

 

 

            

                                                                

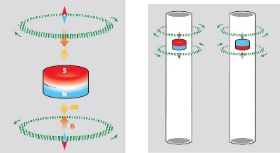
6. Магніт опускають по довгій вертикальній мідній трубі, всередині якої вакуум. Тіла не піддаються стисненню. Описати процес падіння.

Відповідь: У трубі при опущенні магніту в її середину виникає вихровий струм, який тормозить магнітне поле згіднол Правила Ленца. Чим більша швидкість опущення магніта в трубу, тим більша гальмуюча сила. То і прискорення магніта поступово зменшується. Якщо вважати довжину труби дуже довгою, то згодом рух магніта стане рівномірним.

 

 

 

 

 

 

Високий рівень

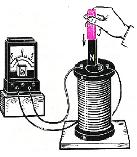7. У замкнену накоротко котушку два рази магніт: перший раз швидко, а другий повільно. Яка кількість теплоти виділиться і чи однаковий заряд пройде по колу в обох випадках?

 

 

 

 

 

 

Відповідь:  спочатку позначимо опір котушки як R.  Тоді індукційний струм знаходитиметься за формулою : . За цей час по колу пройде заряд . Тобто весь заряд, що пройде по колу , буде:, де Ф- кінцеве значення магнітного потоку. Тобто , заряд не залежить від швидкості внесення магніту в котушку. Далі, визначимся з кількістю теплоти в обох випадках. Кількість теплоти Q рівна роботі сторонніх сил . Оскільки, електрорушійна сила пропорційна до швидкості зміни магнітного потоку, то при швидкому внесенні магніту  кількість теплоти, що виділятиметься , буде більшою.

8. Знайдіть різницю потенціалів між двома точками сполучення двох півкілець: одне латунне, інше мідне, при цьому натягнуте на циліндричне осердя того ж радіуса.Півкільця з’єднані так, як показано на малюнку, якщо радіус півкільця 30мм, а індукція в полі зростає зі сталою швидкістю 50 Тл\с.

 

 

 

 

 

 

 

 

 

 

 

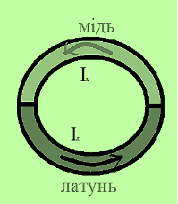
Відповідь:

 

9. Сталевий стрижень завдовжки 40 см і масою 50 г лежить перпендикулярно до горизонтальних рейок. Уздовж рейок напрямлене однорідне магнітне поле індукцією 0,25 Тл. У стрижні пропускають електричний струм силою 2 А. З якою силою стрижень тисне на рейки?

Задачі для самостійного виконання:

1. У якому випадку напрямок ліній індукції магнітного поля прямого провідника зі струмом зазначено правильно?

 

 

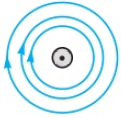
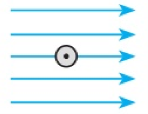
             а)                       б)                                в)                         г)

2.  Укажіть правильний варіант графічного зображення магнітного поля котушки зі струмом.

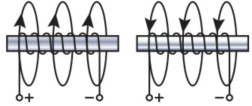
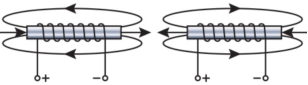
            а)                        б)                            в)                             г)

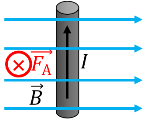3. На рисунку зображено розташування провідника у магнітному полі й позначено напрямок струму та ліній індукції магнітного поля. Укажіть напрямок сили, що діє на цей провідник.

а)Праворуч 

б) Ліворуч

в) До спостерігача

г) Від спостерігача

 

4.      На рисунку зображено провідник зі струмом, розташований у магнітному полі підковоподібного магніту. Визначте полюси магніту.

 

 

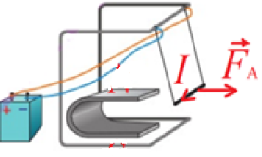
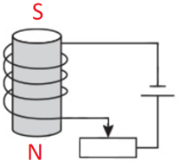
Визначте полюси електромагніта. Як зміниться підіймальна сила електромагніта, якщо повзунок реостата пересунути ліворуч?

електромагніту.

 

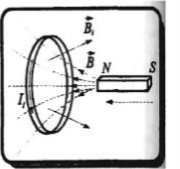5.      Які явища відбудуться, якщо засунути постійний магніт у провідне кільце? У надпровідне?

 

 

 

 

 

 

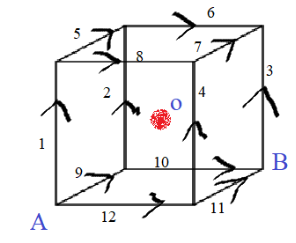
6. Як довести, що магнітна індукція в центрі дротяного куба рівна нулю, якщо до його протилежних вершин, що лежать на одній просторовій діагоналі, підключено джерело струму?

 

 

 

 

 

 

 

 

 

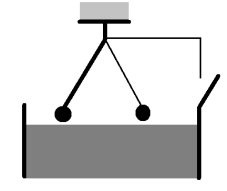
7. Маятник, що складається з металевої кульки, металевої нитки і вістря,занурений в ртуть і робить малі коливання в однорідному магнітному полі. Визначити, як зміняться коливання після замикання кола?

 

 

 

 

 

 

II. Оптика

Методика розв’язування задач з оптики

В основі геометричної оптики лежать уявлення про прямолінійність поширення світла в однорідному середовищі. Напрямок поширення світлових пучків задається за допомогою абстрактної моделі – світлового променя.

На межі двох середовищ спостерігаються явища відбивання і заломлення світла, які описуються відповідно законом відбивання і законом заломлення світла.

На основі закону відбивання світла будуються зображення в плоскому та сферичному дзеркалах.

Зображення предмета, яке утворюється за допомогою плоского дзеркала, завжди є уявним, прямим і дорівнює за величиною розмірам самого предмета. Причиною цього є те, що плоске дзеркало ніколи не змінює кута розхилу світлового пучка, змінюється тільки напрямок його поширення. Паралельні світлові пучки після відбивання у сферичних дзеркалах стають збіжними (вгнуте дзеркало) або розбіжними (опукле дзеркало), тобто змінюється форма пучка. Тому сферичні дзеркала можуть утворювати дійсні і уявні зображення предметів. Опуклі дзеркала завжди утворюють уявні зображення, вгнуті - дійсні або уявні, залежно від розташування предмета відносно фокуса дзеркала. Треба пам’ятати, що дійсним зображенням точки (і предмета) є таке, яке утворюється на перетині відбитих чи заломлених променів, а уявним, якщо воно утворюється на перетині продовження променів в бік протилежний їх поширенню. Щоб розв'язати задачі на закони відбивання світла, потрібно вміти будувати зображення предмета за допомогою дзеркал. Для цього треба знати:

1) закон відбивання;

2) основні точки сферичних дзеркал (рис. 1.1 а,б):

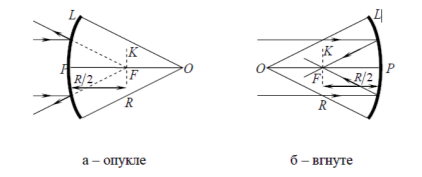
а) оптичний центр О – центр сферичної поверхні, частиною якої є дане дзеркало; б) полюс Р; в) головний фокус F; г) фокусна відстань FР, позначається також F; д) головну оптичну вісь ОР ; е) побічну оптичну вісь ОL; є) фокальну площину FК. Пучок паралельних променів після відбивання від вгнутого сферичного дзеркала (рис. 1.1, б) збирається у фокусі дзеркала F, а після відбивання від опуклого сферичного дзеркала (рис. 1.1,а) розсіюється. Якщо продовжити відбиті промені (показано пунктиром), то вони перетнуться у точці F. Отже, фокус для опуклого дзеркала уявний. Якщо фокус дзеркала є уявним, то в формулі дзеркала перед членом 1/F ставиться знак „–”. Якщо зображення, утворюване дзеркалом, уявне, то знак „–” ставиться також перед членом 1/f. Коли невідомо, яке зображення утворюється за допомогою дзеркала в конкретному випадку, або невідомо, яким є дане дзеркало, у формулі дзеркала перед членом 1/F і 1/f ставиться знак „+”. Якщо знайдена відповідь буде із знаком мінус, то це означає, що зображення є уявним, а дзеркало має уявний фокус.

Відношення розмірів предмета h до розмірів зображення Н знаходять із співвідношення . .

Добуток абсолютного показника заломлення (відношення швидкості світла в вакуумі до його швидкості в даному середовищі середовища на синус кута між променем і перпендикуляром при переході променя з одного середовища в інше є величина стала. Якщо оптична густина одного середовища більша (швидкість світла в ній менша, а показник заломлення більший), то кут між променем і перпендикуляром менший. Якщо промінь попадає на межу двох середовищ, поширюючись з більш густого в менш густе середовище, то можна спостерігати явище повного внутрішнього відбивання, при якому кут в менш оптично густішому середовищі досягає 90°, а кут α (нехай це буде кут в більш оптично густішому середовищі) в цьому випадку одержав назву граничного кута падіння і позначається як α0. В цьому випадку світло не поширюється в менш густому середовищі і повністю відбивається від межі розподілу середовищ, а тому явище і одержало назву повного внутрішнього відбивання. Формула для граничного кута буде мати вигляд

.

Двовгнуту лінзу не можна назвати розсіювальною, а двоопуклу – збиральною. Завжди потрібно враховувати, в яке середовище вміщено лінзу. Якщо абсолютний показник заломлення лінзи менший від цього показника середовища, в яке вміщено лінзу, то .

Збиральну і розсіювальну лінзу умовно позначають значками .

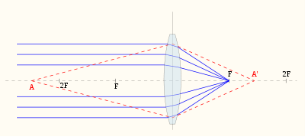
Промені, що попадають на лінзу від дуже віддаленого предмета, можна вважати паралельними між собою. Якщо ці промені паралельні головній оптичній осі, то після проходження збиральної лінзи вони збираються в одній точці F на головній оптичній осі. Ця точка називається головним фокусом лінзи. В разі розсіювальної лінзи промені після лінзи розсіюються, а їх продовження збираються на головній оптичній осі в одній точці. Це буде уявний фокус лінзи (рис. 1.2, а,б).

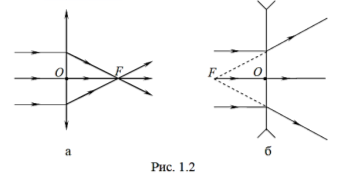
Якщо на лінзу послати пучок паралельних променів, які поширюються вздовж якої-небудь побічної осі (пряма лінія, яка проходить через центр лінзи і не проходить через центри кривизни поверхонь, що утворюють лінзу) МО лінзи (рис.1.3), то вони зберуться в точці F1, яка лежить на перетині побічної осі з фокальною площиною (фокальна площина Р – площина, перпендикулярна головній оптичній осі і проходить через головний фокус лінзи).

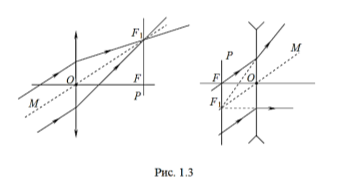
Знаки перед  1/F  і  1/f   у формулі лінзи ставлять так само, як і в формулі сферичного дзеркала. Збільшення зображення, одержаного як за допомогою дзеркала, так і лінзи розраховується по одній і тій же формулі.

Фізична оптика.

В цьому розділі вчення про світло розглядаються властивості світла, його взаємодія з речовиною, в якій відбувається поширення світла, з’ясовується процес поширення світла, фізична природа світла та ін.

У хвильовій теорії світла, яка була основною теорією до кінця ХІХ ст., світло розглядалося як процес поширення поперечних електромагнітних хвиль. Частота ν світлової хвилі монохроматичного світла пов’язана з його довжиною хвилі λ співвідношенням , де – швидкість поширення світла в певному середовищі. 

Максимальну швидкість поширення, яка не залежить від довжини світлової хвилі, має світло у вакуумі. Ця швидкість с=3·10 ^{8 м}/с і є граничною швидкістю протікання процесів в природі. При переході з вакууму в середовище світло змінює свою швидкість поширення і тому відбувається заломлення світлового променя. У будь-яких середовищах найбільшою буде швидкість поширення червоного світла, найменшою – фіолетового.

Відношення швидкості поширення світла у вакуумі с до швидкості поширення світла у певному середовищі υ є абсолютним показником заломлення n цього середовища:

.

Відносним показником заломлення двох середовищ є:

.

Внаслідок того що швидкість поширення світла червоного кольору в середовищі найбільша, абсолютний показник заломлення для довгих світлових хвиль є найменшим. Для фіолетового світла показник заломлення є найбільшим. Тому світло на межі двох середовищ розкладається в спектр- явище дисперсії.

1. Швидкість поширення світла Закони відбивання світла

Швидкість світла — фундаментальна фізична стала, швидкість розповсюдження електромагнітної взаємодії у вакуумі.  c = 299 792 458 м/с.

Закони відбивання:

– падаючий і відбитий промені лежать в одній площині з перпендикуляром, проведеним до відбиваючої поверхні в точці падіння;

– кут падіння дорівнює куту відбивання.

Хід променів при відбиванні світла має властивість оборотності: якщо точковий об’єкт і його зображення поміняти місцями, то хід променів при цьому не зміниться, зміниться лише їхній напрям.

Задачі

Достатній рівень

1. Стовп заввишки 1 метр стоїть вертикально, кидає тінь від ліхтаря довжиною 80см. Яка буде відстань між ліхтарем та стовпом, якщо її збільшити на 1,5 метра, а довжина тіні зросте до 1,3 метри? На якій висоті знаходиться ліхтар?

 

 

 

 

 

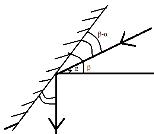
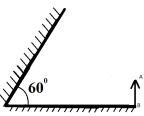
2. Висота Сонця над горизонтом рівна 48^о. Під яким кутом до горизонту слід поставити дзеркало , щоб пустити «зайчика» на дно глибокої криниці?

Відповідь: Спираємось на закони відбивання. З них маємо: β-α=90⁰-β. Спираючись на побудований малюнок, бачимо , що кут β=69⁰.

 

 

 

 

 

Середній рівень

3. Світловий промінь виходить від точки А і приходить в точку В, відбившись від плоского дзеркала. Доведіть, що промінь проходить найкоротшим шляхом!

 

 

 

 

 

 

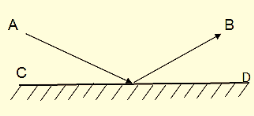
Відповідь: Припустимо, що промінь відбився в якійсь точці Е(див. мал. 1). Траекторія руху променя АЕВ рівна ламаній А1ЕВ, де А1 симетрична А. Довжина цієї ламаної А1ЕВ є найменшою, якщо Е лежить на прямій А1В. То кути СЕА1 і ВЕD рівні як вертикальні,тому кути ВЕF=АЕF, тобто кут падіння дорівнює куту відбивання!

 

 

 

 

 

 

 

 

 

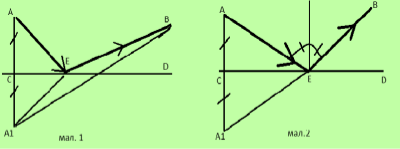
4. Скільки зображень предмета АВ дають дзеркала, розташовані під кутом 60⁰?

 

 

 

 

 

 

 

 

Відповідь: спираючись на малюнок, можна визначити, що: через відбиття світла від першого дзеркала виникає зображення А1 В1, а внаслідок відбиття від другого дзеркала – зображення А2. Після першого відбиття, деякий пучок цих променів ніби виходить з точки А1 у другому дзеркалі, тобто  у цій точці перетинаються продовження променів. То можна стверджувати, що після другого відбиття з’явиться ще одне уявне зображення А3 тіла А1 у другому дзеркалі. Зображення тіла А2 у першому дзеркалі теж потрапляє в точку А3.  Так само відіб’ється А4 і А5. Більше чим два відбиття жоден промінь не зазнає. Тому , зображень буде 5.

 

 

 

 

 

 

 

 

 

 

Високий рівень:

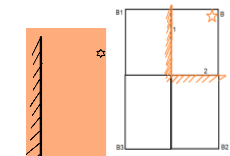
5.      На малюнку схематично зображено будівлю. Перед нею треба поставити ліхтар так, щоб точка 1 потрапила у тінь, а точки 2 і 3 вночі були освітлені ліхтарем. Перемалювати у зошиті цей рисунок і покажіть ділянку можливого розміщення ліхтаря.

 

 

 

 

 

 

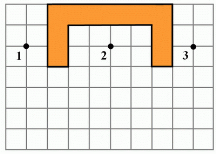
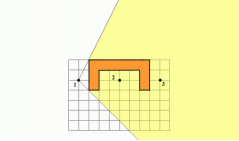
Відповідь:

Перша область - область, з якої не видно точку 1

Друга область - область, з якої видно точку 2

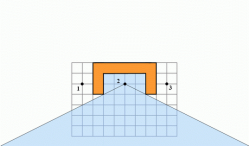
  Третя область - область, з якої видно точку 3

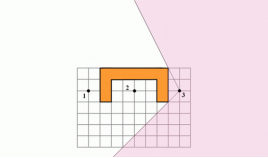
Частина площини, яка є перетином всіх  трьох областей, буде областю, яку потрібно знайти. Знайдемо спочатку перетин першої і третьої області: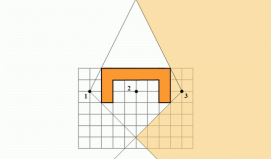

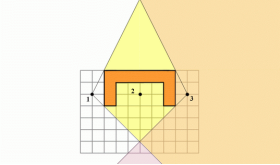
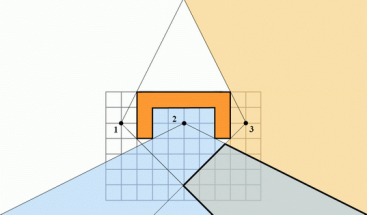
І тепер, перетин отриманої області з другою:

6.      Три дзеркала розташовані так, що між ними утворилися двогранні прямі кути, як показано на малюнку. Як довести, що після трьох відбивань променя світла від цієї системи дзеркал напрямок зміниться на протилежний!?

 

 

 

 

 

 

 

 

 

 

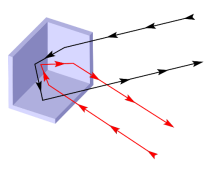
Відповідь: якщо напрямити осі координат вздовж ребер дзеркал, а промінь світла представити у вигляді кульки, яка буде відбиватися від дзеркал, то при кожному з трьох відбиттів одна з проекцій початкової швидкості кульки буде змінювати знак, а інші дві – ні. Після всіх трьох зіткненгь, всі проекції стануть від’ємними, тобто швидкість кульки стане зі знаком «-«. Така властивість тригранного прямого кута використовується в куткових відбивачах – катафотах.

 

Задачі для самостійного виконання

1. Який напис буде видно на аркуші паперу, якщо направити на нього зелене світло?
2. На скляну призму падають два паралельні промені. Чи залишаться ці промені паралельними після виходу з призми?  (Ні)

 

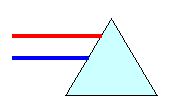
3. Який з цих променів, після проходження крізь призму, заломиться найбільше? (Фіолетовий)

 

 

 

 

 

4.                     Світна точка В знаходиться між двома дзеркалами, які розташовані під прямим кутом. Скільки зображень цієї точки можна побачити в дзеркалах?

 

 

 

 

 

 

 

 

 

 

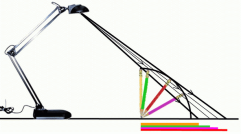
5.                     Олівець має точку дотику до столу і розташований вертикально та освітлюється настільною лампою так,що тінь від нього падає на стіл. Як зміниться розмір тіні від переміщення олівця від лампи до столу? Поясніть ці зміни, виконавши схематичні малюнки ходу променів для кількох положень олівця. Лампу вважайте точковим джерелом світла

 

 

 

 

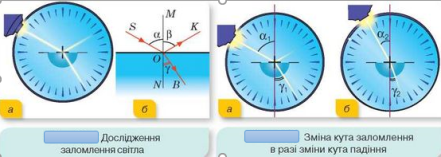
2. Заломлення світла

Заломлення світла — явище зміни напрямку поширення світла в разі його проходження через межу поділу двох середовищ. Причиною виникнення явища заломлення світла є зміна швидкості поширення світла при переході з одного середовища в інше. Як ви вже знаєте, у вакуумі світло поширюється зі швидкістю

У повітрі швидкість поширення світла змінюється незначно, тому вважається, що і для повітря вона становить

 

 

 

 

 

 

Швидкість поширення світла у прозорих середовищах зменшується порівняно зі швидкістю світла в повітрі у відповідну кількість разів: у воді в 1,33 раза;

у склі — майже в 1,6 раза; в алмазі — у 2,4 раза.

Фізична величина, що показує, у скільки разів швидкість поширення світла у вакуумі (с) є більшою, ніж швидкість світла в середовищі (v),

називається абсолютним показником заломлення середовища n

Абсолютний показник заломлення середовища має глибокий фізичний зміст. Він пов’язаний зі швидкістю поширення світла в даному середовищі, яка залежить від фізичного стану середовища (температури, густини тощо). Крім того, показник заломлення залежить від кольору світла: для червоного світла він менший, ніж для зеленого, а для зеленого — менший, ніж для фіолетового. Для будь-якого середовища абсолютний показник заломлення п > 1. Для повітря абсолютний показник заломлення приблизно дорівнює 1.

Із двох прозорих середовищ оптично більш густим називають середовище з більшим показником заломлення, тобто середовище, у якому швидкість поширення світла є меншою.

Отже, можна стверджувати, що вода — більш оптично густе середовище, ніж повітря, а скло чи алмаз — більш оптично густі середовища в порівнянні з водою.

Закон заломлення світла.

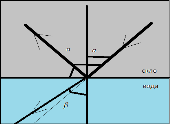
Співвідношення значень кута падіння та кута заломлення у випадку переходу пучка світла з одного середовища в інше залежить від оптичної густини кожного із середовищ. Наприклад, при переході світлового променя з повітря у скло кут заломлення менший від кута падіння

оскільки скло — більш оптично густе середовище, ніж повітря, а при переході світлового променя із скла у воду кут заломлення більший, ніж кут падіння

бо вода — менш оптично густе середовище, ніж скло. Вимірювання кутів падіння та заломлення, співвідношення абсолютних показників заломлення середовищ дозволяють визначити закон заломлення світла:

падаючий промінь, заломлений промінь і перпендикуляр, встановлений до межі поділу середовищ у точці падіння променя, лежать в одній площині;

відношення синуса кута падіння (а) до синуса кута заломлення (g) світлового променя є сталою величиною, яка дорівнює відносному показнику заломлення двох середовищ,

тут n₁ і n₂ - абсолютні показники заломлення першого і другого середовищ, n — відносний показник заломлення.

Задачі

Достатній рівень

1. Промінь світла, виходячи зі скла, заходить у воду і заломлюється на плоскій межі «скло-вода». Який має бути кут падіння, щоб відбитий і заломлений були перпендикулярні?

Відповідь:

 Виходячи із закону заломлення: і рівності

 ,  отримаємо: . Звідси: .

 

 

 

 

 

2. Палиця, закопана в дно озера, піднята ще над водою на 1 метр, а глибина озера – 2 метри. Визначити довжину тіні палиці на поверхні та на дні води, якщо сонце над горизонтом під кутом 30⁰?

Відповідь:

Середній рівень

3. Кут падіння світла на скляну плоскопаралельну пластину рівний 60⁰. Промінь, пройшовши крізь пластину, змістився на 15 мм. Визначити товщину пластини?

Відповідь:

 

 

 

 

 

 

 

 

 

 

 

 

 

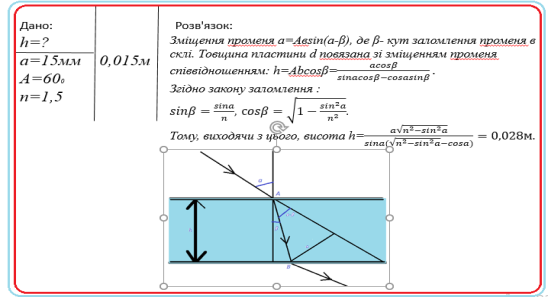
4. У ясний сонячний день водолаз, який стоїть на дні озера, бачить у водному "дзеркалі" у себе над головою відображення всіх ділянок дна, що знаходяться від нього на відстані s = 10 м і більше. Яка глибина Н озера? Зріст водолаза h = 1,7 м.

Відповідь: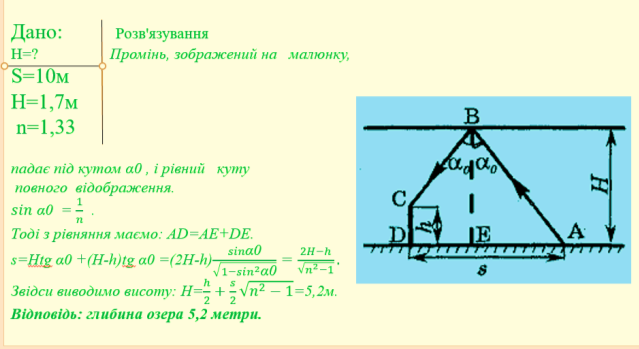

 

 

 

Високий рівень

5. Визначити показник заломлення скипидару і швидкість розповсюдження світла в ньому, якщо відомо що кут падіння променя на поверхню скипидару 45°, а кут заломлення 30°.

Відповідь:

 

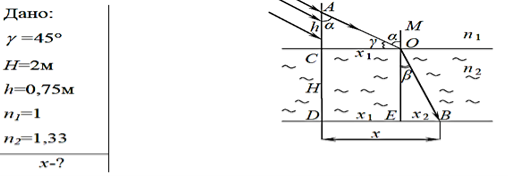
6. На скляну плоскопаралельну пластинку товщиною 2см падає промінь світла під кутом 45°. Показник заломлення скла 1,5. Показати, що промінь, який пройшов через пластинку, паралельний падаючому променю. Знайти віддаль між цими променями.

Відповідь:

 Дано:                                                                       Розв’язання

х-? α=45°           На малюнку бачимо хід променя через

 d=2см                        плоскопаралельну пластинку     товщиною ОЕ=d. Кут падіння α,

  п2=1,5                        кут заломлення β і кут падіння на нижню грань пластинки β.

  п1=1                                    Віддаль між початковим напрямом променя АМ і тим,

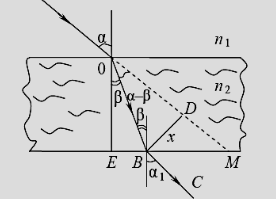                                    яке стало після проходження пластинки (ВС), позначимо через ВD=х (ВD ВС). 

                            Запишемо закон заломлення для верхньої грані пластинки :

                             і для нижньої грані : . (2)

Порівнюючи (1) і (2), приходимо до висновку , а це значить, що промінь ВС||АМ.

З рисунка також видно, що <BOD=α-β

Далі, з EOB:

 

 

Задачі для самостійного виконання:

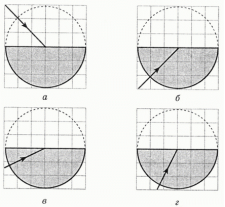1. Побудуйте подальший хід світлового променя, який падає на поверхню скляного півциліндра у випад­ках а-г (див. рисунок). Покажіть як відбиті, так і заломлені промені (якщо вони є).

 

 

 

 

 

 

 

 

 

 

2. Поясніть за допомогою рисунка, чому при погляді зверху глибина води здається меншою, ніж є на­справді.
3. У якому з випадків а-б після збільшення кута падіння можна спостерігати повне відбивання світла?

 

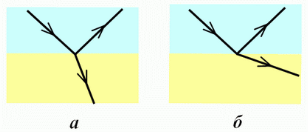
4. Кут падіння вузького пучка світла на поверхню ріди­ни дорівнює 60°, а кут заломлення - 45°. Знайдіть показник заломлення рідини. Під яким кутом до го­ризонту слід розмістити в рідині плоске дзеркало, щоб відбитий пучок повернувся до джерела світла?

 

 

 

 

 

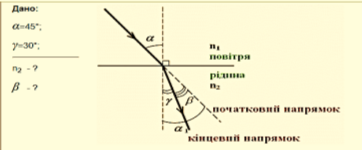
5. Світловий промінь переходить із повітря у прозору рідину. Якщо кут падіння променя становить 45°, то кут заломлення дорівнює 30°. На який кут відхи­ляється промінь від початкового напряму? Знайдіть показник заломлення рідини.

 

 

 

 

 

 

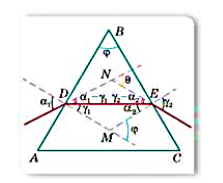
6. Заломний промінь падає під кутом α₁ = 60° на бічну поверхню скляної рівнобедреної призми. Кут при вершині призми φ = 40°. На який кут відхилиться промінь, що виходить із призми, якщо показник заломлення матеріалу призми n = 1,54? Знайти  кут зміщення променя для випадку, коли кут падіння на поверхню призми та заломний кут призми φ — малі.

3. Лінзи. Оптичні системи

Опти́чна лі́нза — найпростіший оптичний елемент, виготовлений із прозорого матеріалу, обмежений двома заломлюючими поверхнями, які мають спільну вісь, або взаємно перпендикулярні площини симетрії. При виготовлені лінз для видимого діапазону світла, використовують оптичне або органічне скло, в УФ діапазоні — кварц, флюорит, і т. д., в ІЧ-діапазоні — спеціальні сорти скла, кремінь, сапфір, германій, ряд солей тощо.

Здебільшого лінзи мають аксіальну симетрію й обмежені двома сферичними поверхнями однакового або різного радіусу.

Оптичні лінзи зазвичай виготовляються зі скла або пластику. Природною оптичною лінзою є кришталик ока.

Лінзу називають тонкою, якщо її товщина мала порівняно з радіусами сферичних поверхонь, що її обмежують. Сферичні тонкі лінзи бувають опуклі і ввігнуті.

Опуклі лінзи мають властивість збирати заломлене світло (кожну з лінз можна умовно розділити на три частини, з яких краї — призми, що заломлюють промені до основи, а середина — плоскопаралельна пластинка), тому їх називають збиральними (у них середина товста, а краї тонші). Ввігнуті лінзи розсіюють світло після заломлення, їх називають розсіювальними (середина тонка, а краї товстіші).

Залежно від розташування центрів сферичних поверхонь та їхнього радіусу розрізняють такі типи лінз

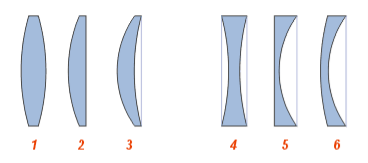1.      двоопукла лінза
2.      плоско-опукла лінза
3.      збиральний меніск
4.      двоввігнута лінза
5.      плоско-ввігнута лінза
6.      розсіювальний меніск

 

В залежності від того, сходяться чи розходяться паралельні пучки променів після проходження лінзи, лінзи поділяють на збиральні й розсіювальні.

Вісь симетрії аксіально-симетричної лінзи називається оптичною віссю. Світловий промінь, який розповсюджується уздовж оптичної осі, не заломлюється.

Важливими характеристиками лінзи є фокусна відстань і обернена до неї величина, яку називають оптичною силою лінзи.

Лінза називається тонкою лінзою, коли її товщина набагато менша за фокусну віддаль. У протилежному випадку, коли товщиною лінзи не можна знехтувати в порівнянні з фокусною віддаллю, лінзу називають товстою.

Головний фокус

 

Збиральна лінза має властивість збирати промені, випущені з однієї точки, в іншій точці з іншого боку лінзи. Якщо на деякій відстані перед лінзою розмістити точку А, то промені, що виходитимуть із цієї точки, проходитимуть через лінзу, заломлюючись до оптичної осі, і збиратимуться в точці А'. Ця точка називається спряженим фокусом до точки А.

Якщо віддаляти точку А від лінзи, то точка А' переміщатиметься ближче до лінзи, і навпаки.

Якщо точка А знаходитиметься нескінченно далеко від лінзи, то промені від неї будуть паралельними, а точка А' називатиметься головним фокусом лінзи, а відстань до неї — головною фокусною відстанню.

Площини, що проходять через головні фокуси лінзи перпендикулярно до її головної оптичної осі, називають фокальними площинами лінзи. Точки перетину побічних оптичних осей з фокальними площинами лінзи називають побічними фокусами лінзи.

Зображення, утворене лінзою

При побудові зображень створених двоопуклою лінзою, проводять три лінії:

1.      Із вершини предмета паралельно оптичній осі лінзи до головної площини лінзи, далі, заломлюючись, через задній головний фокус.
2.      Із вершини предмета через центр лінзи.
3.      Із вершини предмета через передній фокус до головної площини лінзи, а далі паралельно оптичній осі лінзи.

Ці три лінії перетинаються в одній точці і дають зображення вершини предмета. Відповідно до формули: {\displaystyle {\frac {1}{S_{1}}}+{\frac {1}{S_{2}}}={\frac {1}{F}}}

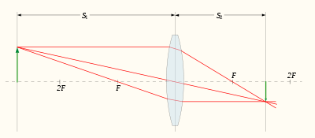
1.      Якщо предмет знаходиться далі за подвійну фокусну відстань, то зображення знаходитиметься позаду лінзи між фокусом і подвійним фокусом і буде дійсним, перевернутим і зменшеним.
2.      Якщо предмет знаходиться між фокусом і подвійним фокусом перед лінзою, то зображення буде позаду лінзи за подвійним фокусом і буде дійсним, перевернутим і збільшеним.
3.      Якщо предмет знаходиться ближче від фокуса перед лінзою, то зображення буде ще ближче перед лінзою і буде уявним, прямим і збільшеним.

Задачі

Достатній рівень

1. На кожному з малюнків показано головну оптичну вісь тонкої лінзи MN, світну точку А та її зображення А₁. Зобразити за допомогою побудов, де буде оптичний центр лінзи та фокуси. Знайти тип лінз та тип зображень!

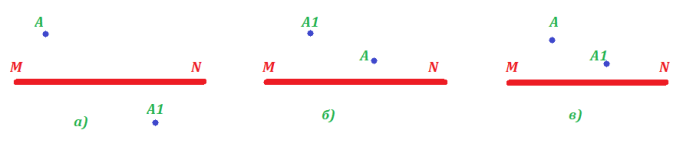
Відповідь: через точку А1 проходять промені , що вийшли з точки А і заломались в лінзі. У нашому випадку варто скористатись двома променями: променем, що проходить через оптичний центр та променем, паралельним головній оптичній осі.

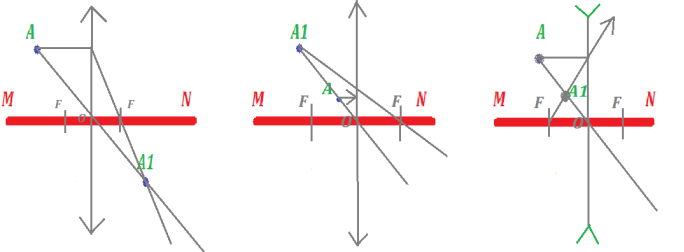З малюнків видно: перше зображення дійсне, 2 і 3 уявне.

 

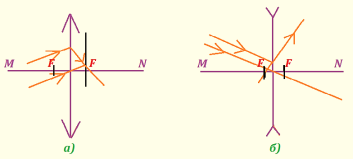
2. На головній оптичній осі NM лінзи побудовано хід променів. Побудувати положення фокусів.

 

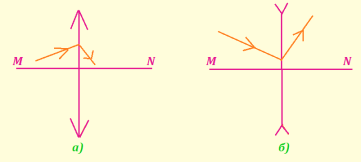
Відповідь:  якщо на лінзу падають паралельні промені, то після проходження через лінзу ці промені перетинаються у фокальній площині. То маємо такі продовження:

 

 

 

 

Cередній рівень

3.                На якій відстані від обличчя потрібно тримати вгнуте сферичне дзеркало з фокусною віддаллю 30 см для того, щоб одержати збільшене у п’ять разів зображення обличчя?

 

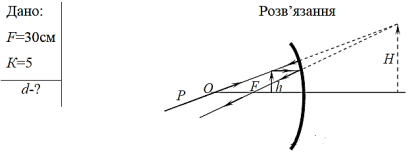
Відповідь:

У формулі перед другим членом потрібно взяти знак «-«, бо зображення в нашому випадку буде уявним. Отже, .  З формули

  знаходимо . Знаючи, що і значить а тому . Звідси

Відповідь: на відстані 24 см потрібно поставити дзеркало.

Високий рівень

 

4. Точковий предмет рухається по дузі кола з швидкістю υ1=3см/с навколо осі збиральної лінзи в площині, що перпендикулярна до головної оптичної осі лінзи і віддалена від лінзи на відстані d=1,5F, де F – фокусна відстань лінзи. В якому напрямку і з якою швидкістю υ2 рухається зображення предмета?

Відповідь:

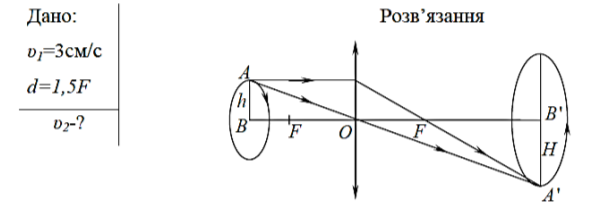На малюнку бачимо рух предмета по дузі. Знайдемо звязок висотою зображення А'В΄ і висотою предмета АВ, які позначимо через Н і h. Як відомо збільшення зображення знаходиться за формулою i .

З формули лінзи маємо: .

Знайшовши f підставляємо в К: . Якщо точка А рухається в площині, перпендикулярній головній оптичній осі, по колу радіуса h, то зображення буде рухатись по колу радіуса Н. Як видно з рисунка напрямок швидкостей у точки і її зображення протилежний. За один і той же час (наприклад, період Т) точка пройде шлях, рівний довжині кола радіуса h, а її зображення – довжині кола радіуса Н. Тобто,

 .

Таким чином швидкість руху зображення .

Задачі для самостійного розвязання:

1.                Якої висоти потрібно взяти плоске дзеркало, щоб людина могла себе в ньому побачити на повний зріст?

 

 

 

 

 

 

 

 

 

 

 

 

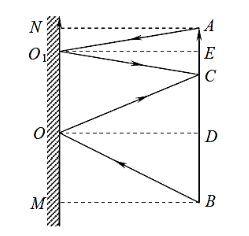
2. Відстань між предметом і його прямим збільшеним у два рази зображенням, одержаним за допомогою тонкої лінзи, дорівнює L. Знайти оптичну силу лінзи і з’ясувати характер зображення (дійсне чи уявне).

 

 

 

 

 

 

 

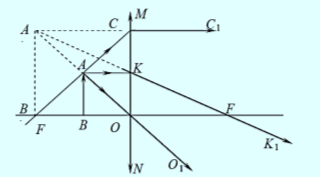
3. Плоске дзеркало рухається з швидкістю 1,5 см/с. З якою по модулю і напрямом швидкістю повинно рухатись точкове джерело світла, щоб його зображення в плоскому дзеркалі було нерухомим?

 

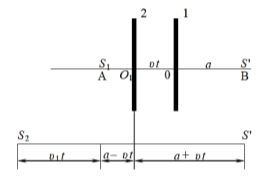
4. В дно водоймища глибиною 2 м забита свая, що виступає над поверхнею води на 0,75 м. Знайти довжину тіні від сваї на поверхні води і на дні водоймища, якщо висота Сонця в даний момент 45°.

 

ІІІ. Магнетизм

Методика розв`язування задач

Коливаннями або коливальними рухами називають такі види механічного руху чи зміни стану системи, які періодично повторюються з часом. Механічні коливання – періодичне переміщення тіла то в один, то в другий бік відносно положення рівноваги. Механічна система, в якій одне або декілька тіл можуть здійснювати коливальні рухи, називають коливальною системою або осцилятором. Коливання, які відбуваються лише під дією внутрішніх сил, називають вільними. Щоб система виконувала ці коливання, треба вивести тіло з положення рівноваги, тобто надати коливальній системі енергію. Вільні коливання поділяються на незгасаючі (у відсутності сил тертя) та згасаючі (у середовищі з опором). Коливання під дією зовнішньої сили, що періодично змінюється, називають вимушеними. Коливання називають періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим прикладом періодичних коливань є гармонічні коливання, під час яких фізична величина змінюється з плином часу.

Хвилею називають процес поширення коливань у просторі з часом. Механічна хвиля – це процес поширення механічних коливань у пружному середовищі. Якщо джерело хвиль знаходиться в пружному середовищі, що займає досить велику частину простору, тобто в суцільному середовищі (твердому тілі, рідині або газі), всі точки якого між собою пружно зв'язані, то збудження коливань частинок біля джерела зумовлює вимушені коливання сусідніх частинок, ті, в свою чергу, збуджують коливання наступних тощо. Якщо частинки пружного середовища коливаються в площині, перпендикулярній до напряму поширення хвилі, то таку хвилю називають поперечною. Ця хвиля може поширюватися в твердих тілах або на поверхні рідин. Якщо частинки середовища коливаються в тій самій площині, в якій поширюється і сама хвиля, то хвилю називають поздовжньою. Така хвиля поширюється в твердих тілах, рідинах і газах. Геометричне місце точок середовища, до яких дійшов хвильовий процес у даний момент часу, називається фронтом хвилі. Хвильовою поверхнею є геометричне місце точок, що коливаються в однаковій фазі. Хвильових поверхонь багато, а хвильовий фронт тільки один. Періодом T хвилі є період коливань точок середовища під дією цієї хвилі. Частотою  хвилі називають величину, обернену періоду, яка дорівнює кількості коливань, здійснених за 1 с.

В однорідному середовищі хвиля поширюється рівномірно і прямолінійно. Швидкість поширення коливань v у просторі називають швидкістю хвилі. Найкоротша відстань між точками хвилі, які коливаються в однакових фазах, називають довжиною хвилі . Довжина хвилі дорівнює відстані, яку пробігає хвиля за один період коливань   vT=v/ʋ.

Розглянемо пружне середовище, між частинками якого існують сили взаємодії Тіло, яке коливається в пружному середовищі, періодично діє на прилеглі до нього частинки середовища, виводячи їх з положення рівноваги і змушуючи здійснювати вимушені коливання. При цьому середовище поблизу тіла деформується і в ньому виникають пружні сили. Ці сили діють як на прилеглі до тіла частинки, намагаючись повернути їх у положення рівноваги, так і на віддаленіші від тіла частинки, виводячи їх з положення рівноваги. Віддаленіші від тіла області середовища поступово втягуються в коливальний рух.

Основна властивість всіх хвиль є перенос енергії без переносу речовини.

5. Механічні коливання та хвилі

Пружними (або механічними) хвилями називаються поширення коливань у пружному середовищі. Механічні (пружні) хвилі бувають поперечні і поздовжні.

Рис. 1 Поперечна механічна хвиля

 

У поперечних хвилях частинки середовища коливаються в площинах, які перпендикулярні до напрямку поширення хвилі (рис. 1). Поперечні хвилі можуть поширюватись в середовищі, в якому виникають пружні сили при деформації зсуву, тобто лише у твердих тілах.

Рис.2 Поздовжня механічна хвиля

У поздовжніх хвилях частинки коливаються в напрямку поширення хвилі (рис. 2). Ці хвилі можуть поширюватись в середовищах, в яких виникають пружні сили при деформації стиску і розтягу, тобто у твердих, рідких і газоподібних тілах. 

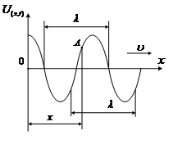
Нехай поперечна  хвиля поширюється вздовж осі Ох.

 

Відстань між найближчими частинками, що коливаються в однаковій фазі, називається довжиною хвилі λ. 

Довжина хвилі дорівнює тій відстані, на яку поширюється певна фаза коливань за період:

λ = uT,  

або

u = λν.

Нехай точка, від якої йдуть коливання, коливається в суцільному середовищі. Коливання поширюються від центра у всі боки. 

Хвиля називається сферичною, якщо її хвильові поверхні мають вигляд концентричних сфер. Центр цих сфер називається центром хвилі.

Інші характеристики механічних хвиль:

- Швидкість хвилі – це швидкість поширення коливань у просторі. Позначається швидкість літерою u та вимірюється у метрах, поділених на секунду.

- Довжина хвилі – відстань між найближчими одна до одної точками хвилі, які коливаються в однаковій фазі. Довжина хвилі позначається літерою λ та вимірюється у метрах.

- Період – мінімальний проміжок часу, за який відбувається одне коливання. Період позначається літерою Т та вимірюється в секундах.

- Частота хвилі – частота коливання частинок середовища. Позначається літерою ν та вимірюється в герцах. Частота обернено пропорційна періоду.

Задачі

Достатній рівень

1. На озері з човна в безвітряну погоду скинули якір. Дослідник, який стояв на березі, полічив, що хвиля досягла берегу за 1 хв, а за 10 с відбувся 21 сплеск, рахуючи з першого. Відстань між сусідніми гребенями хвиль становила 0,7 м. Визначте відстань від човна до берега?

Відповідь:

                                    Розв'язання

Відстань між сусідніми гребенями — це довжина хвилі. За 10 с відбувся 21 сплеск, рахуючи з першого, тобто частинки води за 10 с здійснили 20 повних коливань (дослідник почав відлік часу, коли перший гребінь вже досяг берегу, а закінчив, коли берега досяг 21-й гребінь).

Відстань, на яку поширюється хвиля, дорівнює: s = vt₁.

За формулою хвилі v = λv , де v = .

Отже, маємо:

s = vt₁ = vt₁ = λ ∙  ∙ t₁ ; s = (0.7*20*60)/10 = 84 (м).

Відповідь: 84 м.

2. Математичний маятник довжиною 1 м коливається з амплітудою 1 см. За який час він пройде шлях в 1 см, якщо в початок свого руху він виходить з положення рівноваги? За який час він пройде половину свого шляху? За який час здійснить другу половину свого шляху?

Відповідь:  

 

 

 

 

 

 

 

 

Середній рівень

3. Знайти період та частому математичного маятника, якщо його довжина 1 метр?

Відповідь:

 

 

 

4. Період коливань математичного маятника дорівнює 1 с. Визначте довжину маятника.

Відповідь:

 

 

 

 

 

 

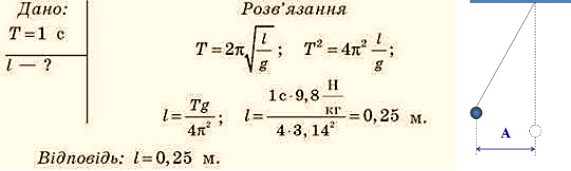
Високий рівень

5. Радіолокатор працює на хвилі 5 см і випускає імпульси тривалістю 1,5 мкс. Скільки коливань міститься в кожному імпульсі? Яка мінімальна дальність виявлення цілі ?

Відповідь:

Дано:                                     Розвязання:

N=?                                  

lmin=?                                =9000

λ=5см=5*10^-2м                Відбитий радіосигнал приймається

                                         тільки після закінчення

t=1,5мкс=1,5*10^-6с      випромінювання наступного імпульсу.

                                     

Відповідь:9000 коливань, дальність цілі 225м.

 

 

Задачі для самостійного розвязання:

1.                Порівняйте періоди коливань математичного маятника довжиною 1 м на Землі і на Місяці. Прискорення вільного падіння на Місяці вважати таким, що дорівнює 1,62 Н/кг.
2.                Коливальний контур радіоприймача настроєний на частоту 6 МГц. У скільки разів треба змінити ємність конденсатора контуру, щоб настроїтися на довжину хвилі 150м ?
3.                Гоночний автомобіль з включеною сиреною мчить зі швидкістю 306 км / год. Частота коливань сирени 400 Гц. Попереду і на узбіччі стоїть інший автомобіль з точно такою ж увімкненою сиреною. Кожен з водіїв розрізняє звук сирени іншого автомобіля, тому що він вище, ніж звук його власної сирени. Хто з них чує більш високий звук? Яка частота цього звуку?

 

6. Електромагнітні коливання і хвилі

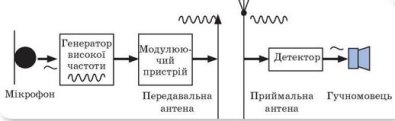
Джерелом електромагнітної хвилі може бути тільки пристрій, у якому створюються електромагнітні коливання високої частоти.

Електромагнітна хвиля як процес поширення електромагнітно­го поля насамперед характеризується вектором напруженості Е та вектором магнітної індукції В. Будь-яка хвиля періодична і в часі, і в просторі, тому ці величини періодично змінюються і з часом, і зі зміною відстані від джерела хвилі.

Електромагнітна хвиля — це поперечна хвиля.

Електромагнітна хвиля, як і механічна, характеризується періодом і частотою коливань, довжиною та швидкістю поширення.

Швидкість поширення електромагнітної хвилі — це відстань, на яку поширюється електромагнітна хвиля за одиницю часу.

Швидкість поширення електромагнітних хвиль у вакуумі є ста­лою й дорівнює швидкості світла у вакуумі.

Довжина хвилі — це відстань, на яку поширюється електромагніт­на хвиля за час, що дорівнює періоду; або: відстань між двома най­ближчими точками в просторі, в яких коливання вектора напруженості (вектора магнітної індукції) відбуваються однаково.

 

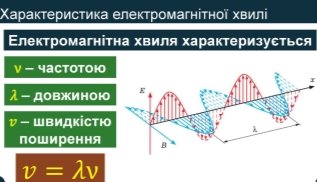Період- це час одного коливання.      =1с.       N-кількість коливань за час t.

Частота-кількість коливань за одиницю часу.       ==1 Гц=с^-1   ν= .Зв’язок періоду з частотою  .      ;  .      . Амплітуда-максимальна відстань, на яку відхиляється тіло від положення рівноваги.

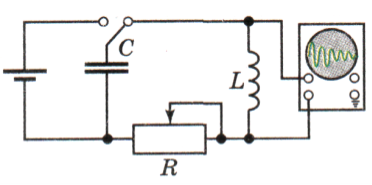
Колива́льний ко́нтур або коливний контур — електричне коло, складене з резистора, конденсатора та котушки індуктивності, в якому можливі коливання напруги й струму. Коливальні контури широко застосовуються в радіотехніці та електроніці, зокрема в генераторах електричних коливань, в частотних фільтрах. Вони використовуються практично в кожному електротехнічному пристрої.

Послідовний RLC-коливальний контур: V - напруга в контурі І - сила струму в контурі R - резистор L - котушка індуктивності C - конденсатор

 

Задачі

Достатній рівень

1. Сергій захоплюється біологією. Якось готуючи повідомлення до уроку, він знайшов в мережі інтернет інформацію про те,  що павуки великі меломани. Тобто, якщо поблизу житла павука грати на якомусь музичному інструменті, він вилізе і буде насолоджуватися  музикою. Як з точки зору фізики  пояснити таку любов павуків до музики?

 Розв'язання. Звук від музичного інструмента викликає коливання павутини, і павук вилазить на  помилковий сигнал своєї здобичі.

Середній рівень

2. Коливальний контур радіоприймача фіксовано налаштовано на приймання сигналу радіостанції, що випромінює радіохвилі завдовжки 2,4 м. Радіоаматор вирішив переналаштувати приймач на приймання сигналу іншої радіостанції і послідовно приєднав до конденсатора в коливальному контурі конденсатор утричі меншої ємності. Визначте (у метрах), на яку довжину хвилі тепер налаштовано радіоприймач.

Розв'язання

З формули хвилі c = λv маємо:  λ= , де

v = .

3. Під час риболовлі спостережливий Артем нарахував 120 коливань поплавка за 2,5 хвилини. Він також помітив, що відстань між сусідніми гребенями хвиль приблизно дорівнює 1,5 м. Визначте швидкість поширення хвиль на поверхні води.

Розв'язання. Скориставшись формулою швидкості поширення хвилі та частоти

маємо: .

Звідки: .

Високий рівень

4. Частота коливання голосових зв'язок чоловіка, що говорить басом, змінюється в межах від 80 до 350 Гц. Яка довжина випромінюваної звукової хвилі?

Розв'язання. λ = , де