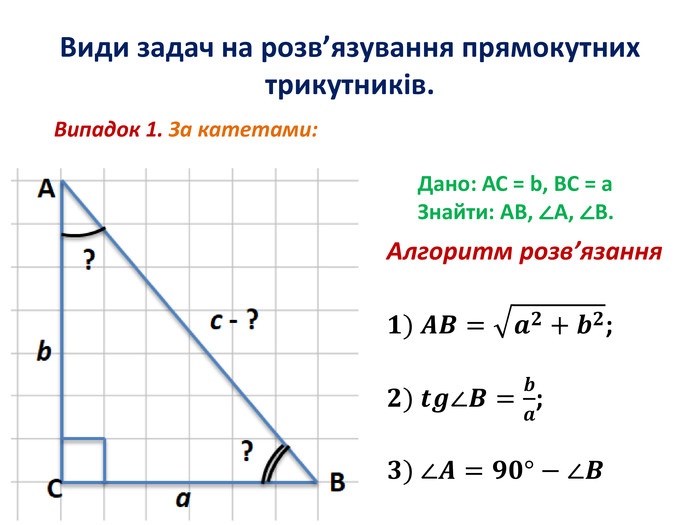
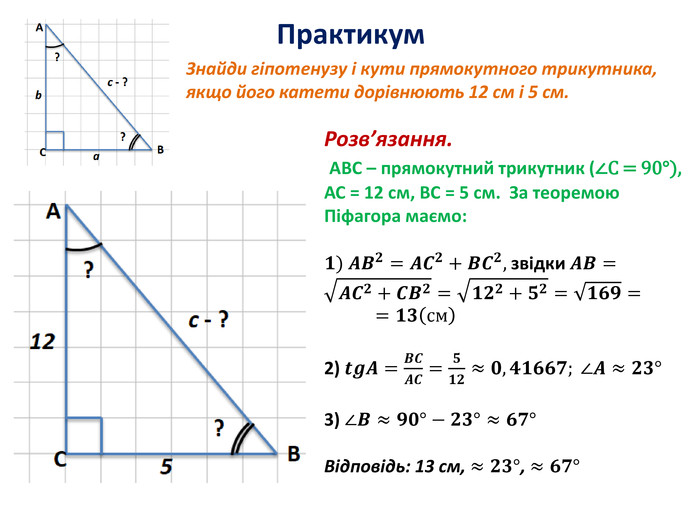
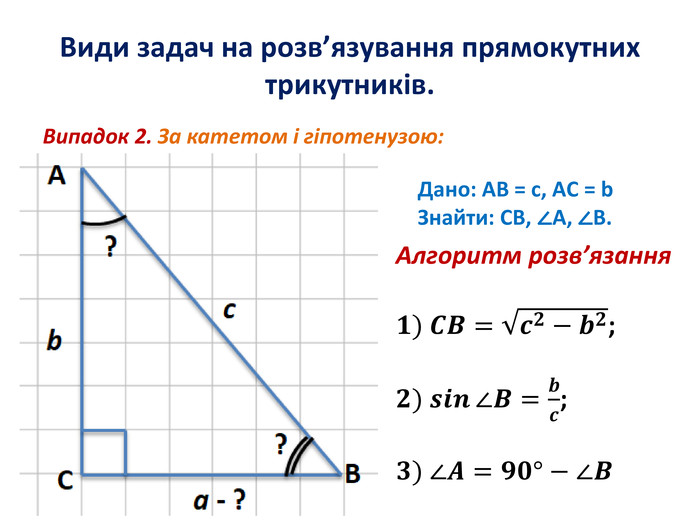
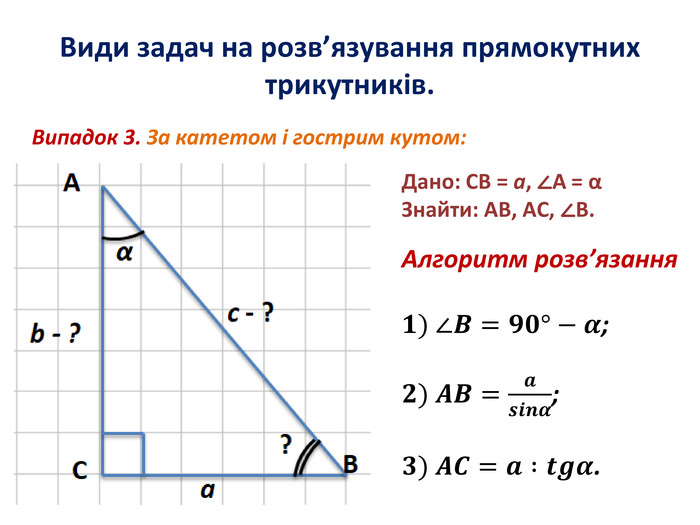
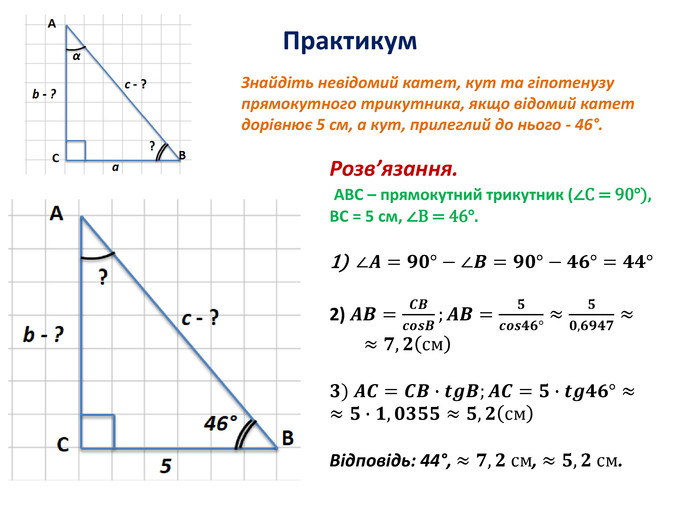
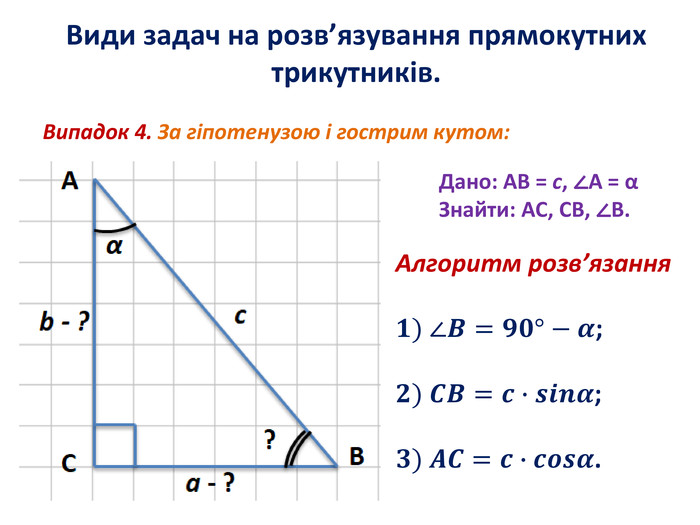
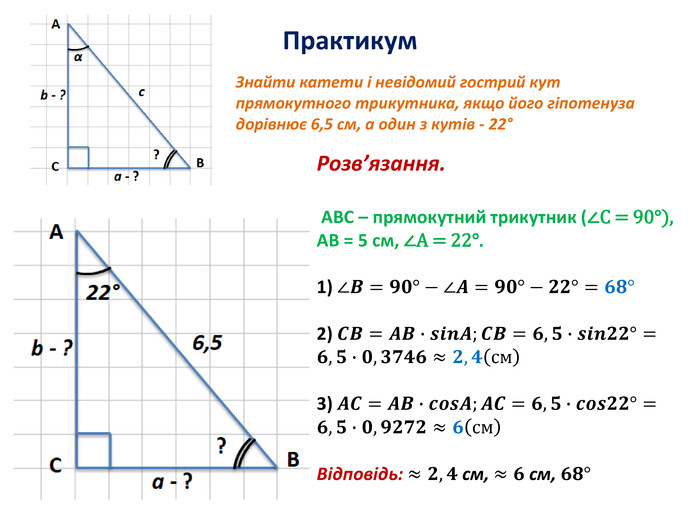
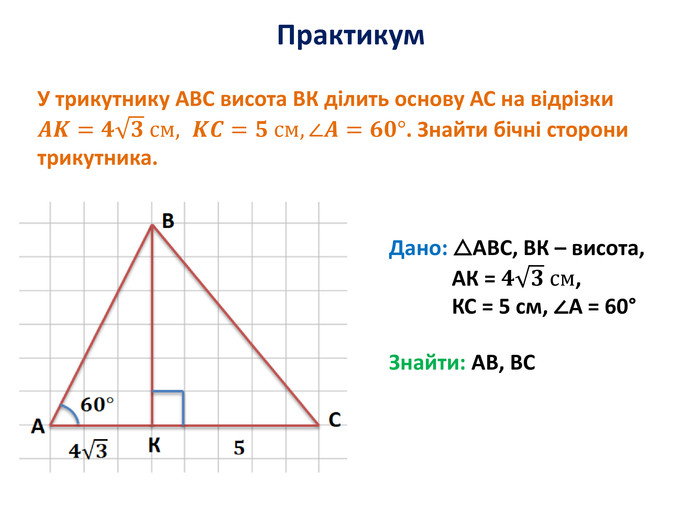
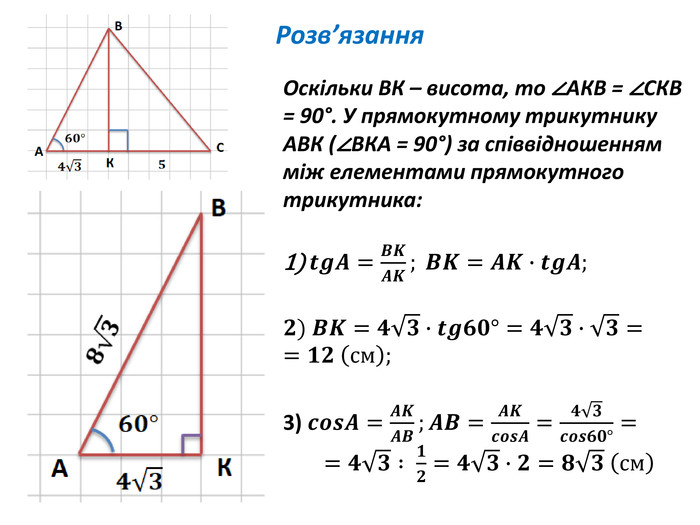
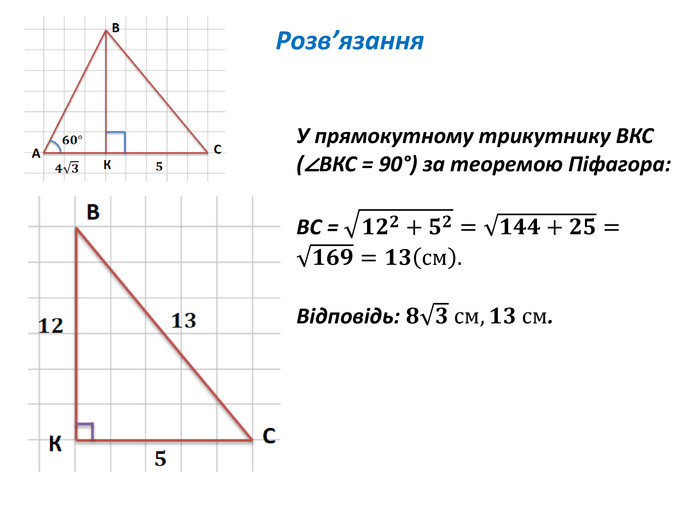
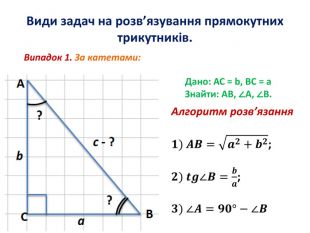
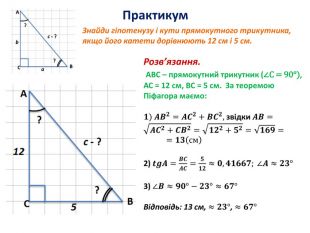
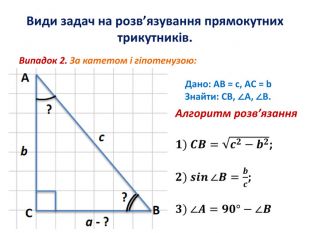
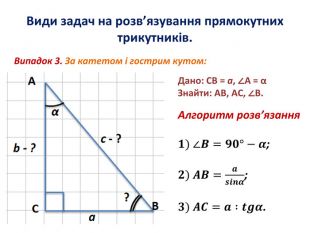
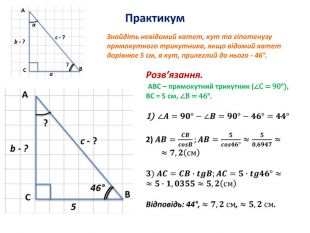
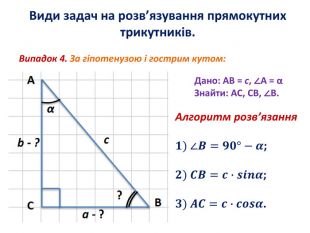
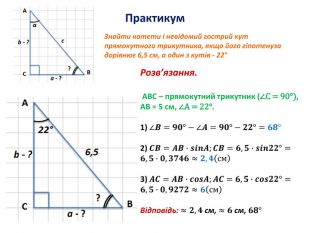
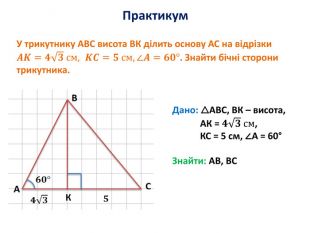
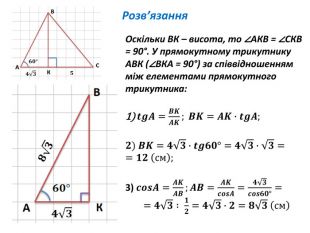
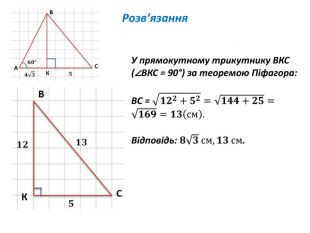
Розв'язування прямокутних трикутників
Про матеріал
Матеріал до уроку може бути використаний під час дистанційного навчання, або при поясненні нового матеріалу
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку