Розв'язування рівнянь

Урок № ____       Дата: _________________                                              Клас: 5

Тема: Числові вирази. Буквені вирази та формули

Мета: сформувати уявлення учнів про поняття «числові вирази» та «бук­вені вирази»; навчити розпізнавати числові і буквені вирази, читати їх; виро­бити вміння знаходити значення виразів за умови різних значень змінної; розвивати пам'ять, логічне мислення, вміння пояснювати дії, розвити пізнавальний інтерес; виховувати наполегливість, увагу, зосередженість.

Тип уроку: засвоєння нових знань.

Обладнання: картки.

Хід уроку

І. Організаційний момент

(Заходжу до класу). Добрий день діти! Сідайте. (Перевіряю стан дошки, наявність вологої ганчірки, крейди, відмічаю відсутніх).

ІІ. Перевірка домашнього завдання

Для перевірки домашнього завдання здаємо зошити.

ІІІ. Актуалізація опорних знань

Але перш ніж почати давайте повторимо означення і розв’яжемо усно декілька прикладів.

1. Які числа називаються натуральними числами?
2. Які ви знаєте види натуральних чисел?
3. Які числа називають кількісними?
4. Які числа називають порядковими?

Усні вправи

Завдання завчасно записані на дошці.

1. Обчисліть:

а) 12 + 16;   б) 39 – 24;   в) 18 · 2;

г) 39 : 3;   д) 75 + (25 + 13);  є) 75 – (25 + 13);

є) (36 + 19) – 16;  ж) (36 + 19) – 19;  з) (47 + 18) – (17 + 8).

2. Поставити замість знака «?» пропущені слова і числа.

Молодці! Дуже добре впоралися з цими завданнями, а зараз відкрили свої зошити, записали число, класна робота та тему нашого уроку.

ІV. Мотивація навчальної діяльності

Слова учителя:

У всьому світі люди передають різноманітні відомості, виража­ють свої думки й почуття, тобто обмінюються інформацією за допо­могою мови. На сьогодні існує багато — близько 2000 — різних мов, якими пишуть, говорять та читають різні народи. Ці мови — при­родні, бо вони виникли й розвивалися разом з народами.

Вивчаючи математику, ви поступово знайомитеся з мовою ма­тематики, яка вважається штучною мовою, бо вона створювалася і розвивається разом із самою наукою. Основою математичної мови є цифри та математичні знаки: · : = > < + - , ( ) тощо.

У математичній мові також використовуються латинські букви. Сьогодні ми з вами познайомимося з різними видами виразів.

 V. Засвоєння нових знань

Бесіда.

— Скільки пальців на одній руці?

Варіанти відповідей:

1) 5;

2) 3 + 2;

3) 8 – 3;

4) 2 · 2 + 1;

5) (2 + 1) · 2 – 1.

Усе це різні записи одного й того ж числа 5. Кожен з них є числовим виразом або просто виразом.

Числовий вираз складається з чисел, знаків дій і дужок. Знаки дій і дуж­ки показують, які дії і в якому порядку потрібно виконувати над числами, що входять до числового виразу. Виконавши усі дії, отримаємо значення виразу.

Нехай маємо числові вирази:

(10 – 5) · 7;  (6 – 5) · 7;   (8 – 5) · 7.

— Чим схожі і чим відрізняються ці вирази?

— Скільки ще подібних виразів можна записати?

— А чи можна ці вирази записати за допомогою одного виразу з бук­вою?

Запис (k – 5) · 7 — буквений вираз. Він складається з чисел, букви, зна­ків дій і дужок.

Якщо в буквеному виразі замість букв поставити певні числа, то мати­мемо числовий вираз.

Вирази, які містять знаки арифметичних дій, можна читати, використо­вуючи назви цих дій.

Приклад.

Сума 7 і а: 7 + а;

різниця 7 і а: 7 – а;

добуток 7 і суми 3 і а: 7 · (3 + а);

частка від ділення суми 7 і 3 на а: (7 + 3) : а.

Якщо буквений вираз позначити деякою буквою, то рівність, одна частина якої містить цю букву, а друга містить буквений вираз, становитиме формулу.

 Наприклад, формула шляху має такий вигляд: S дорівнює добутку v і t, де s – пройдений шлях, v – швидкість, t – час, тобто, щоб знайти пройдений шлях, треба швидкість помножити на час руху.

Із формули можна виразити будь-яку букву, що входить до неї. Із формули пройденого шляху випливає формула швидкості: v дорівнює частці S і t, тобто, щоб знайти швидкість, треба пройдений шлях поділити на час руху.

 Із формули шляху випливає і формула часу: t дорівнює частці S і v, тобто, щоб знайти час руху, треба пройдений шлях поділити на швидкість руху.

V. Закріплення матеріалу

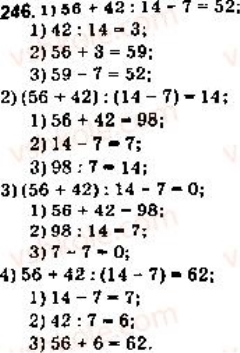
VI. Підбиття підсумків

Отже, ми з вами розглянули нову тему, а зараз дайте відповідь на наступні запитання.

Що ви дізналися нового?  Що вам було незрозуміло? Що вам сподобалось?

VІI. Домашнє завдання

Опрацювати §2 п. 9. Розв’язати № 248, 250, 252.