Розв’язування системи n лінійних рівнянь з n невідомими методом Крамера і методом Гауса.
Практична робота
Розв’язування системи n лінійних рівнянь з n невідомими
методом Крамера і методом Гауса.
Мета уроку: Формувати навички і вміння розв’язувати системи лінійних рівнянь методами Крамера і Гауса.
Актуалізація опорних знань:
- Що називається системою m лінійних рівнянь з n невідомими?
- Яка система рівнянь називається сумісною, несумісною; визначеною, невизначеною?
- За яких умов однорідна система лінійних рівнянь має єдиний нульовий розв´язок ; безліч розв´язків?
- Назвати елементарні перетворення матриці.
Алгоритм методу Крамера
Знайти ![]() - визначник основної матриці системи, складений з коефіцієнтів при невідомих.
- визначник основної матриці системи, складений з коефіцієнтів при невідомих.
Знайти ![]() - визначники матриці, які утворюються з основної матриці системи заміною j стовпця стовпцем вільних членів.
- визначники матриці, які утворюються з основної матриці системи заміною j стовпця стовпцем вільних членів.
Обчислити корені системи за формулою ![]() .
.
Завдання 1 Розв’язати систему рівнянь методом Крамера

Розв’язування:
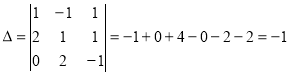 ;
;
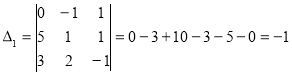 ;
;
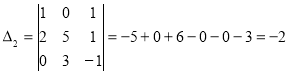 ;
;
 ;
;
![]() ;
; ![]() ;
; ![]() .
.
Відповідь. ![]() .
.
Алгоритм методу Гауса
Помноживши перше рівняння на необхідні числа і додавши одержані рівняння відповідно до другого, третього,..., n–го рівнянь, вилучаємо х1 з усіх рівнянь, починаючи з другого.
Помноживши друге рівняння на необхідні числа та додавши одержані рівняння відповідно до третього, четвертого,..., n–го рівнянь, вилучаємо х2 з усіх рівнянь, починаючи з третього.
Таким самим способом вилучаємо всі решта невідомі: х3, х4,...,хn-1. Останнє рівняння буде рівнянням з одним невідомим.
Починаючи з останнього рівняння, по черзі знаходимо всі невідомі.
Завдання 2 Розв’язати систему рівнянь методом Гауса
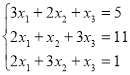
Розв’язування:
До першого рівняння, яке множиться на (-2), послідовно додаємо друге і третє, які множаться на 3. Отримамо рівносильну систему, у якій в другому і третьому рівняннях виключено ![]() . До третього рівняння додаємо друге, помножене на 5. Отримамо східчасту систему , з якої послідовно знаходимо
. До третього рівняння додаємо друге, помножене на 5. Отримамо східчасту систему , з якої послідовно знаходимо ![]() ,
, ![]() і
і ![]() .
.
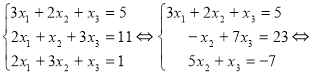
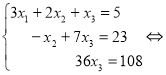
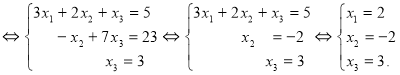
Відповідь: ![]()
Систему лінійних рівнянь зручно розв’язувати, використовуючи матричну форму запису.
Наприклад: 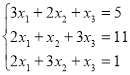
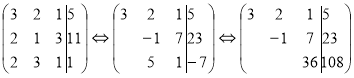
Звідси ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() .
.
Відповідь: ![]() .
.
Вправа для самостійного розв’язання
Розв’язати систему рівнянь методами Крамера і Гауса.
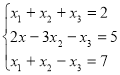


про публікацію авторської розробки
Додати розробку
