Презентація "Розв'язування тригонометричних нерівностей"
Про матеріал
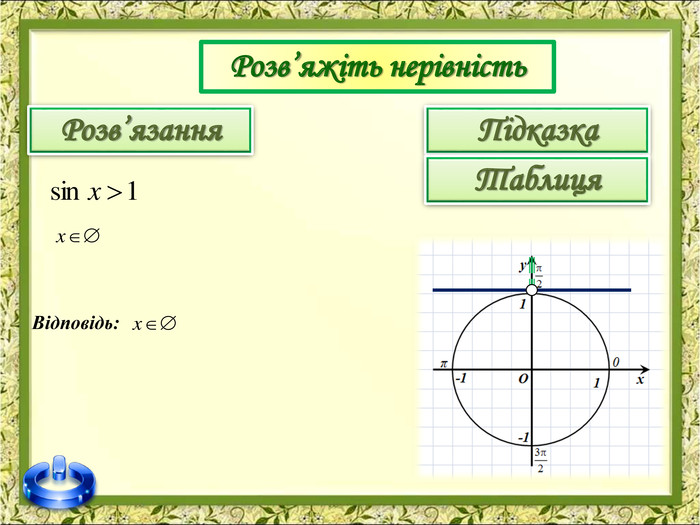
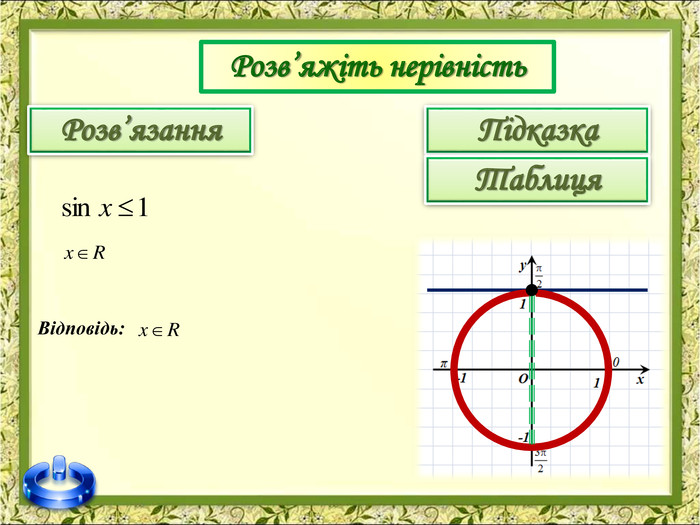
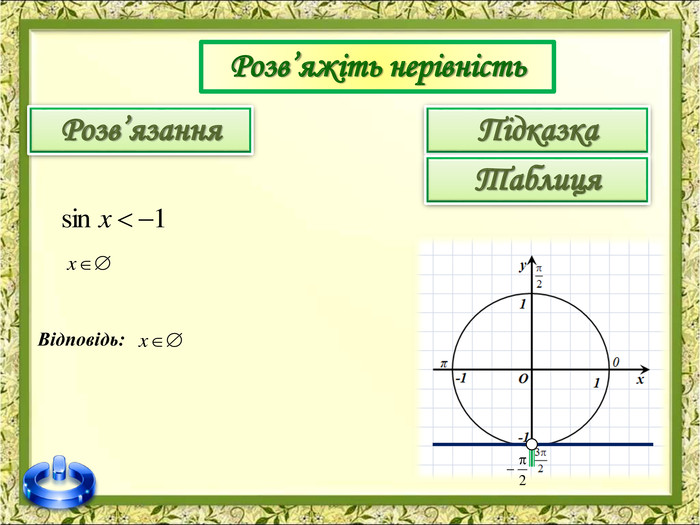
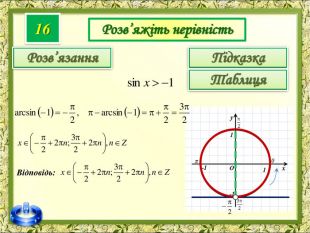
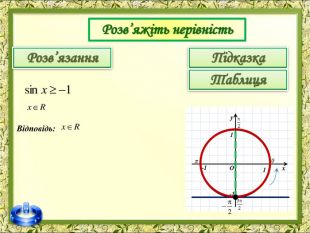
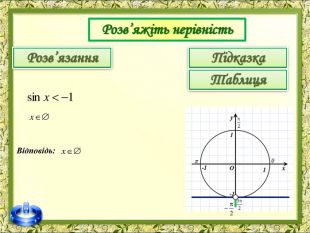
До вашої уваги пропоную презентацію з теми "Розв'язування тригонометричних нерівностей"
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку