Розв’язування тригонометричних рівнянь

Тема. Розв’язування тригонометричних рівнянь

Мета. Формування вмінь та навиків розв’язувати тригонометричні рівняння,    навчити раціонально вибирати метод їх розв'язування; удосконалити уміння правильно розв'язувати найпростіші тригонометричні рівняння. Розвивати навички самоконтролю та взаємоконтролю, логічне мислення, пам’ять, вміння аналізувати ситуацію; творчі здібності та пізнавальну активність.

Завдання. Оволодіти  різними методами розв’язування тригонометричних  рівнянь

Обладнання.     Дидактичний матеріал, проектор.

Урок-саміт

   Хід уроку

Слайд 1

Титульна сторінка «Тригонометрії» (перевидання 1612 року) В.Пітіска, що дала назву однойменному розділу математики

1. Організація уроку.

Доброго всім дня та хорошого настрою. Запишіть у зошитах

16 квітня

Класна робота

2. Актуалізація опорних знань.

На попередніх уроках ми ознайомилися з тригонометричними рівняннями та формулами розв’язків найпростіших тригонометричних рівнянь.

Слайд 2

Запитання.

• Які рівняння називаються тригонометричними?
• Що означає розв’язати рівняння?
• Яка особливість розв’язків тригонометричних рівнянь?
• Які тригонометричні рівняння називаються найпростішими?
• Що називають арксинусом числа  a ?
• Що називають арккосинусом числа  a?
• Що називають арктангенсом числа  a ?
• Що називають арккотангенсом  числа  a ?

3. Мотивація навчальної діяльності учнів.

Сьогодні ми проведемо урок- саміт « Розв’язування тригонометричних рівнянь».  Перед нами стоїть завдання оволодіти  різними методами розв’язування тригонометричних рівнянь. Для реєстрації в саміті необхідно виконати тестові завдання.

Слайд 3

Тести

1. Яке з рівнянь не має розв’язку?

 а)  sin х = 0,7;    б) sin х = 1,3;

в)  sin х = - 0,25;            г) інша відповідь.

2. Розв’язати рівняння:  cos х =

а) + 2πп, n є Z;      б)  - + πп, n є Z;

в) ±  + 2πп, n є Z;      г) інша відповідь.

3. Обчислити:  arccos ( - )

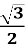а)       ;                     б)  -     ;

в)      ;                            г) інша відповідь.

4. Розв’язати рівняння:  tg х = 1

а) +2πп, n є Z;         б)    ;

в)  + πп, n є Z;         г) інша відповідь.

5. Розв’язати рівняння:  sin х = 0

а) (-1)ⁿ  +2πп ; n є Z;  б)  + πп n є Z;

в)  πп, n є Z;            г) інша відповідь.

6. Обчислити:  acrctg ( -)

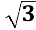а)  -;    б)  -;

в)                 г) інша відповідь.

      Учні обмінюються тестами і перевіряють. Відповіді зображені на слайді.

Слайд 4

1. б)

2. в)

3. а)

4. в)

5. в)

6. б)

3. Формування вмінь та навичок учнів.

На порядку денному : тригонометричні рівняння та способи їх розв’язування.

Слайд 5

Завдання. Оволодіти  різними методами розв’язування тригонометричних  рівнянь

Слайд 6

 Розрізняють такі види тригонометричних рівнянь

-найпростіші тригонометричні рівняння;

-тригонометричні рівняння, які зводяться до найпростіших;

- однорідні тригонометричні рівняння.

Слайд 7-9

Найпростіші тригонометричні рівняння;

 

Переходимо до виконання завдання

Розв’язати рівняння

 

Слайд 10

Завдання 1.

     4 cos² x   +  sinx  = 1      

  Деякі тригонометричні рівняння можна привести шляхом тотожних перетворень до рівнянь з однією тригонометричною функцією, потім зробити заміну і привести рівняння до алгебраїчного.

 

Слайд 11

Завдання 2.

sinx + cosx = 0

 

Значення х  при cos x=0, не задовольняє даному рівнянню, бо тоді й sin x теж дорівнював би нулю, а cos x і sin x не можуть одночасно дорівнювати нулю. Тому можна розділити обидві частини рівняння почленно  на cos x.

 

Завдання 3.

sin² x - 3 sin x cos x + 2 cos² x = 0

Слайд 12

Завдання 4.

sin² x -5 cosx= sinx cosx -5 sinx

Багато тригонометричних рівнянь, права частина яких дорівнює нулю, розв’язуються розкладанням лівої  частини на множники.

Слайд 13

Завдання 5.

1+ cos 4x=cos 2x

Слайд 14

 Підказка        1+cos2 x =2cos² x

Слайд 15 робота в групах    Слайд 16-18

4. Рефлексія. Підсумок уроку.

Клас поділений на три групи. Кожній групі дано завдання визначити, яким чином розв’язати дане рівняння. Представник кожної групи  після обдумування дає відповідь.

І група

1. 2cos 2x + 3sin 2x = 0
2. 2 sin² x - 5 sin x cos x + 3 cos² x = 0
3. 6 sin²3 x + sin3x cos 3x - cos² 3x = 2
4. 2 sin² x + cos² x = 5 sin x cos x

ІІ група

1. sin²3 x =
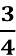
2. cos 2x cos х + sin 2x sin х = 1
3. tg x – 2ctg x + 1 = 0
4. sin3 x - sin x = 0

            ІІІ група

1. sin² x + sin x cos x = 0
2. sin 2 x + cos x =0
3. sin3 x - sin x = 0
4.  1+ cos6х= 2 cos3х

Слайд 19

Виділимо сновні методи розв’язування тригонометричних рівнянь:

• зведення рівняння до квадратного;
• зведення до однієї тригонометричної  функції;
• розкладання на множники;
• використання тригонометричних формул
• однорідні тригонометричні рівняння

 

5. Застосування набутих знань у житті.

Без рівняння немає математики як засобу пізнання природи.

 

6. Домашнє завдання.

Повторити п. 15,16,17. Виконати завдання  №17.8

А.Г. Мерзляк та інші Математика,10