Урок "Тригонометричні функції. Математичне моделювання екологічних процесів." 10 клас

Алгебра і початки аналізу. 10 клас.

Тема уроку :   Тригонометричні   функції.  Математичне  моделювання   екологічних

                         процесів.

 – розвивати логічне мислення учнів;

Тип уроку : урок узагальнення та систематизація знань.

Обладнання : мультимедійне обладнання,презентація вчителя.

Епіграф уроку  :  «В кожній природничій науці укладено стільки істини, скільки в

                                 ній є математики»      

                                   И. Кант

                                                                     Хід уроку :

І.Організаційний момент.

 Повідомлення теми, мети та плану уроку.

II. Мотивація навчання.

Учитель :

Епіграф нашого уроку :

«В кожній природничій науці укладено стільки істини, скільки в ній є математики» И. Кант.

Серед багатьох глобальних проблем розвитку людської цивілізації, які виникли в другій половині XX століття є і такі, що стосуються як усього людства, так і кожної людини зокрема.

Одна з таких проблем – охорона навколишнього середовища, тобто охорона води, повітря, ґрунту і всього живого на Землі.

Часто ці питання називають проблемою збереження екологічної рівноваги біосфери.

Давайте згадаємо, що означає термін « Екологія».

Термін  « екологія» складається з двох грецьких слів : oikos – оселя,   logos –наука, тобто буквально – наука про оселю. Термін   „ екологія "   впроваджений у вжиток німецьким біологом  Ернстом Геккелем в 1866 р.

Запитання до учнів :

Який розділ математики був частиною астрономії, потім став самостійним розділом, а пізніше перетворився в навчальний предмет ? Про що йдеться ?

Відповіді учнів : про тригонометрію.

Учитель :

Які задачі, ще на зорі цивілізації були поставленні перед нашими пращурами ? І що допомагає людству захистити і зберегти навколишнє середовище в наш час ? Доповідають учні.

III. Математичне   моделювання   процесу   зміни   температури   за   допомогою тригонометричної функції.

Застосовуємо інтерактивну технологію  „ Вирішення проблем ”

Учитель :

Використання   математичного   моделювання   в   екології   дає   змогу   по-іншому поглянути на більшість традиційних проблем цієї науки .

Розглянемо приклад застосування тригонометричних функцій до моделювання періодичних процесів, що спостерігаються в природі.

Взагалі точних періодичних процесів у природі не дуже багато, але близькі до періодичних зустрічаються досить часто .

Зокрема, зміна температури повітря, води в річках та поверхні Землі відбувається по роках, по сезонах і протягом доби .

Зараз ми з вами виконаємо математичне моделювання процесу зміни температури.

Задача

Відомо, що літньої днини найвища температура повітря, яка дорівнює 25° С , досягається опівдні, а найвища температура, що дорівнює 15° С, спостерігається опівночі, тобто в нуль годин ( або о 24 годині).

Суть проблеми – визначити тригонометричну функцію, яка може наближено описати процес зміни температури Т протягом доби .

Учні вирішують цю проблему і приймають колективне рішення .

Обговорення проблеми :

Згадується загальний вигляд синусоїдальної ( гармонічної ) функціональної залежності:

                    (1)

Застосовуються додаткові умови, що випливають з постановки задачі:

              Т(0) = 15° С ;  Т(12) = 25° С ;  Т(0) = Т(24) = 25° С   (2)

З умови (2) учні знаходять, який період повинна мати функція (1), він дорівнює 24.

Знаходиться мінімальне і максимальне значення функції (1), відповідно 15 і 25 .

Обчислюється частота    ,     (3)

Синус набуває найменшого значення при ,  тоді початкова фаза :

       (4)

Шукана функція має такий вигляд :

Учні ставлять перед собою питання : як знайти А і В ?   З'ясовують , що за допомогою додаткових умов (2), можна скласти систему рівнянь :

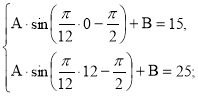
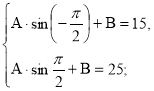
Знайшли невідомі параметри А і В,  А = 5,  В = 20   (5).

Підставляють значення (5)   у рівність (1), шукану функцію записують в такому остаточному вигляді:

.

На  мультимедійній дошці  показана   послідовність   побудови   графіка   функції

:

   мал.1

                 мал.2

     мал.З

  мал.4

Учитель запитує учнів :

Які геометричні перетворення графіків функцій були використані ?

Учні відповідають :

мал. 1 – побудова графіка функції у = sin t ;

мал. 2 – паралельне перенесення графіка функції у = sin t на   вправо у напрямі осі

ОХ,  отримаємо графік   у

мал. З – розтяг графіка функції   в 5 разів від осі ОХ, отримаємо графік

функції , розглянемо  паралельне  перенесення      графіка     функції

у   вздовж  осі  ОУ  вгору   на  20  одиниць,  отримаємо   графік   функції

мал.4 –  розтяг  графіка  функції    від  осі ОУ  в 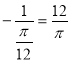  разів ,

отримаємо графік функції

Учитель :

Подібним способом за допомогою тригонометричних функцій описують також інші

періодичні процеси.

IV. Робота в парах

Учитель :

Пропоную вам  наступне  завдання : визначити тригонометричну функцію, яка може

наближено описати процес  зміни  температури  протягом  доби  від  – 4 °С до  12°С,

тобто : Т(0) = Т(24) =  – 4 , Т(12) = 12 .

Це   завдання   виконується  за  5   хвилин.   За   цей  час  ви  обговорюєте  завдання ,

розв'язуєте. По закінченні часу на обговорення кожна  пара  представляє  результати

роботи, обмінюється своїми ідеями та аргументами з усім класом .

Розв'язання задачі:

Т(0) = Т(24) = – 4 ;  Т(12) = 12 .

;

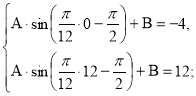
Після розв’язування цієї задачі обговорили результати роботи в парах , обмінялися своїми ідеями та аргументами .

V. Підведення підсумків уроку.

На підсумковому етапі уроку учням пропонується відповісти на запитання.

•    Що нами зроблено на уроці ?
•    Що     людство     використовує    для     розв’язання    проблеми     навколишнього середовища ?

•    Який приклад моделювання екологічних процесів,  що  спостерігають  у  природі ,

ми розглянули сьогодні на уроці ?

•    Що стало зрозумілим після розв'язування цієї задачі ?

Учитель оголошує оцінки, коментує їх .

Задає  домашнє  завдання.

Пропонує учням відповісти на таке запитання :  

• Яка  ж людина ,  на  ваш  погляд ,  може   практично   допомогти   в   розв’язанні

екологічних проблем і зберегти природу , яка радує людське око своєю красою ?

Учні відповідають на це запитання і згадують слова, які були сказані  на  засіданні

ООН:

«Ми не успадковуємо Землю від наших батьків, ми беремо її у борг у наших дітей».