Розв'язування задач на обчислення площ многокутників

Тема уроку: Розв’язування задач на обчислення площ многокутників.

Мета уроку: узагальнити та систематизувати знання учнів про площі многокутників; продовжити удосконалювати навички і вміння знаходити площі многокутників; розвивати творчі здібності учнів шляхом розв'язування різних типів задач; показати зв'язок геометрії з життям; виховувати інтерес до математики, уміння спілкуватися.

Тип уроку: Урок узагальнення і систематизації знань.

Обладнання: Мультимедійний проектор, картки із завданнями, ноутбук.

Епіграф уроку:

«Розумова праця на уроках математики - пробний камінь мислення»

В. О. Сухомлинський.

Хід уроку

 І. Організаційний момент.

Доброго дня, мої дорогі учні! Ми знову зібралися разом на уроці геометрії.

Урок щоб легко нам почати,

Слова важливі прошу пам'ятати,

Що Божа ласка душу очищає

І розум благодаттю наповняє

Тож з Богом до вершин

Математичних знань крокуємо,

Бо математика то храм науки

І в ньому ми пануємо,

Щасливий той, хто увійшов до нього,

Він мудрим став і знає що до чого,

Подаруйте один одному посмішку. А я бажаю кожному з вас, щоб на цьому уроці ви були:

 «У» - уважними;

«С» - спокійними;

 «П» - працелюбними;

«І» - ініціативними;

«Х» - хоробрими;

А одним словом, я бажаю вам УСПІХУ! І не тільки на уроках геометрії, бо як зазначав філософ Е.Ільєнко: «Усе людське життя – це не те, що інше, як постійне бажання досягти успіху у вирішенні питань і проблем».

ІІ. Мотивація навчально-пізнавальної діяльності.

На попередніх уроках ми з вами вивчили формули, за допомогою яких обчислюються площі многокутників, вчилися розв’язувати задачі, використовуючи набуті теоретичні знання. Тема сьогоднішнього уроку: «Розв’язування задач на обчислення площ многокутників». Мета уроку: узагальнити та систематизувати знання учня про площі многокутників; продовжити удосконалювати навички і вміння знаходити площі многокутників.

ІІІ. Актуалізація опорних знань.

Дайте відповіді на запитання:

1)    Що таке площа многокутника? Сформулюйте властивості площі.

2)    Чому дорівнює площа прямокутника? Квадрата? Прямокутного трикутника? Трикутника?

3)    Записати формулу Герона для обчислення площі трикутника.

4)    Чому дорівнює площа паралелограма?

5)    Чому дорівнює площа ромба, якщо відомі його діагоналі?

6)     Чому дорівнює площа трапеції?

7)     Одиниці вимірювання площ.

ІV. Перевірка домашнього завдання.

Дано: ABCD-рівнобічна трапеція (BC II AD)

AB=CD=10 см. MNперпендикулярнеAD, MN=8см.

Знайти: S_ABCD.

Розв’язання:

Оскільки в трапецію вписано коло, то AD + BC=AB + CD =10 + 10=20(см).

S_ABCD*MN*8=80()

Відповідь: 80

 

 

V. Формування навичок умінь.

Сьогоднішній урок можливо, покажеться незвичайним для вас, але я хочу продовжити його оповідання Л.М. Толстого «Чи багато людині землі потрібно».

     Подивіться на малюнок (проектується на екран). На ньому зображено бідного селянина, який стоїть на одній нозі, бо має такий маленький клаптик землі, що другу ногу й поставити ніде.

     Зміст оповідання Л. Толстого такий. Роками мріяв селянин Пахом про власну землю. Довго гроші складав, відмовляючи собі в усьому. І ось, нарешті зібрав заповітну суму.

      Старшина поставив йому таку умову:

- Скільки за день землі обійдеш, уся твоя буде за 1000 крб., але коли до заходу сонця не повернешся на місце, з якого вийшов, пропали твої гроші.

      Тільки зійшло сонце, вирушив Пахом від мітки Пахом від мітки. Пройшов верст 10, вирив яму й звернув круто вліво. Пройшов по цій стороні ще більше, верст 13, загнув другий кут. Третьою стороною пройшов усього 2 версти, глянув на сонце, - воно вже низенько, а до мітки ще верст 15 буде. Вирив ямку і став навпростець поспішати. Іде, іде, важко йому стало, відпочити хочеться, але не можна: сонце вже зовсім низько. Прискорив ходу, а мітка ще далеко. Побіг риссю. Біжить, сорочка до тіла липне, в роті пересохло, серце молотком б’є глянув, сонце вже заходити починає. Додав ходи з останніх сил. Прибіг до місця, упав, руками до мітки дістав.(Під час розповіді проектується малюнок).

 

 

 

 

 

-Ну й молодець! Багато землі придбав!- вигукнув старшина.

Підбіг слуга, щоб допомогти Пахому підвестись, але той уже мертвий лежав...

Завдання 1

За малюнком обчисліть площу і периметр земельної ділянки, яку обійшов Пахом.

Площу фігури можна обчислити двома способами:

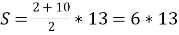1. =78
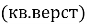
2. S=S₁+S₂

 

Учитель. А якби 40 верст Пахом пройшов по сторонах квадрата, яку площу він би обійшов?

Учні обчислюють спочатку сторону квадрата, а потім його площу:

а = 40/4 = 10 (верст)

S = 10 * 10 = 100 (кв.' верст)

Учитель. Ось вам пропоную розглянути таблицю і зробити висновок.

Завдання 2

Периметр	Р	40
Сторона прямокутника	a	10	8	6	4	2	1
	b	10	12	14	16	18	19
Площа	S	100	96	84	64	36	19

 

Висновок. Якщо  периметр прямокутника сталий,то з усіх прямокутників з цим периметром найбільшу площу має квадрат.

 

Учитель.  Якби Пахом знав цю властивість, він міг би пройти, наприклад, усього 36 верст і в результаті обійти ділянку більшої площі:

P=9 4 = 36 (верст)
        S=99= 81 ( кв. верст)
 

Можливо тоді оповідання не мало б такого трагічного кінця.

Верста – давня міра відстаней, яка вживається  в Україні, Росії, Білорусії, Польщі. У різний час верста була різної довжини – від 500 до 1000 сажнів. З  XVIIІ ст. у Росії і Україні 1 верста дорівнювала 500 сажням (
Учитель. Ви, діти, можете сказати, що  я цією задачею висвітлила  неактуальну тему, але мета моя була довести вам настільки важливі в житті знання математики. Сподіваюся , ви зрозуміли, що вміння  розв’язувати математичні задачі часто полегшує життя, а іноді – й зберігає його.

VI Самостійна робота

I варіант
Квадрат і ромб мають мають рівні периметри . Площа якої фігури більша? Чому?
 

 

 

 

 Розв’язання

Нехай сторона квадрата і ромба дорівнює a. Тоді площа квадрата дорівнює a² , а площа ромба a, де h – висота ромба, що є катетом прямокутного трикутника з гіпотенузою a, тобто h<a . Отже a² >ah. Площа квадрата більша за площу ромба .

 

II варіант

Паралелограм і прямокутник мають рівні основи і рівні периметри. Площа якої фігури більша? Пояснити.

Розв’язання:

Нехай сторони прямокутника a і b. Тоді його площа a*b. Сторони паралелограма також дорівнюють a і b, але площа його дорівнює ah, де – h катет прямокутного трикутника з гіпотенузоюb, b>h. Отже ab>ah. Площа прямокутника більша.

Розв'язування задачі за готовим малюнком.

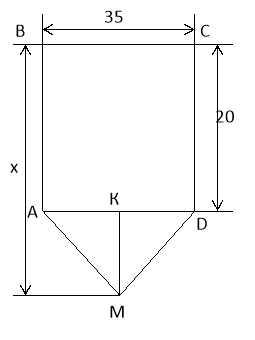Площа фігури, зображеної на малюнку, дорівнює 805. Знайти невідомий розмір х.

 

 

 

 

 

 

 

 

 

 

 

Розв’язання:

Розберемо фігуру на  дві фігури.

S_ABCD = 35‧20 =700 ().

S_ADM= 805-700=105 ().

Проведемо МК – висоту ADM. MK=(X-20)см.

S _ADM=

105= (x-20);

;

x-20=6

Відповідь: 26 см.

 

2) Сторони трикутника АВС дорівнюють:

АВ=14 см, ВС=13 см, АС=15 см. Знайти радіус кола, центр якого лежить на стороні АВ і яке дотикається до двох інших сторін трикутника.

                             Дано: АВС=14см., ВС= 13см., АС=15см.

Знайти: ОМ. ОК

 

 

Розв’язання: S_ABC =(см).

S_ABC==

=

З іншого боку SABC =SAOC+SBOC.

Нехай OM=OR=r.

S_ABC=

Дано: АВСD­   -прямокутник.   ВК     АС

АК=2см ,   

КС =8см

Знайти:

 

= AB∙BC.

AB ====2(см)

BC = ===4(см)

= 2 ∙ 4 = 8 ∙ 5 = 40(см)

Відповідь: 40.

А зараз ми з вами розгадаємо невеличкий кросворд. Ключове слово кросворда ви прочитаєте у виділеному стовпчику.

1.                   Сторона прямокутного трикутника (гіпотенуза);
2.                   Паралелограм з прямими кутами (прямокутник);
3.                   Фігура з рівними сторонами. (Квадрат).
4.                   У чотирикутнику живуть,

Із кута у протилежний кут ідуть.

Ми їх в задачах зустрічаємо.

І як ми ці відрізки називаємо? (Діагоналі).

5.                   Три точки невеличкі

Відрізками сполучимо,

А те, що утворилося,

Всі разом ми озвучимо. (Трикутник).

6.                   Геометрична фігура. (Трапеція).

 

Вчитель.Це слово – «знання». Це така вершина, до якої ми прагнули дійти сьогодні і до якої ви повинні прагнути усе житя. Як сказав Абу-ль-Фарадж: «Знання-настільки дорогоцінна річ ,що її не ганебно добувати з будь-якого джерела»

 

Підсумок уроку:

На цьому уроці ми систематизували і узагальнили знання з даної теми.

Продовжіть фразу:

- Сьогодні  на уроці я закріпив…

- Сьогодні на уроці я повторив…

- Сьогодні на уроці я познайомився..

- Сьогодні на уроці я дізнався…

   А працюючи разом ви досягли успіху.

    У кожній справі є доробок…

  А у народі зветься він жнива

 А в нас сьогодні підсумок по темі

 Це бал високий і знання.

 

Виставлення оцінок.

Домашнє завдання.

1.                   Повторити теоретичний матеріал по даній темі.

   2.Розв’язати: ставок має форму квадрата.Біля його

  вершини ростуть дуби. Як збільшити площу ставка, щоб   збереглася його форма і дуби не опинилися воді?

 

2.                   Вправа № 811

Вчитель. На закінчення уроку хочу сказати вам такі слова:

Бажаю всім присутнім

Я успіхів, удачі

Приходьте на уроки

Розв’язуйте задачі.