Рівнобедрений трикутник. Властивості та ознака рівнобедреного трикутника. Розв’язування задач.

Рівнобедрений трикутник. Властивості та ознака рівнобедреного трикутника. Розв’язування задач.

Мета:

навчальна: узагальнити та систематизувати знання учнів з теми «Рівнобедрений трикутник. Властивості та ознака рівнобедреного трикутника», продовжити формування вмінь та навичок розв’язування задач з теми;

виховна: виховувати в учнів інтерес до вивчення предмету через ілюстрацію

практичної значимості вивченого  матеріалу;

розвивальна: розвивати логічне мислення, математичне мовлення, увагу,

пам'ять, навички самоконтролю знань, пошуку та аналізу інформації

використовуючи ІКТ при роботі в групах та парах.

 

Тип уроку: урок узагальнення та систематизації знань

 

Обладнання: конспект уроку, підручник, презентація учительська та учнівська, мультимедійний екран, набір слайдів, креслярські інструменти, таблиця, набори трикутників, картки самооцінювання для учнів, дидактичні роздаткові матеріали.

 

Структура уроку:

І. Організаційний момент.

ІІ. Мотивація навчальної діяльності учнів.

ІІІ. Повідомлення теми, мети та завдань уроку.

ІV. Перевірка домашнього завдання.

V. Актуалізація опорних знань учнів.

VІ. Розв’язування задач.

VІІ. Підбиття підсумків уроку.

VІІІ. Оцінювання роботи учнів на уроці.

ІХ. Повідомлення домашнього завдання.

 

Хід уроку

 

Природа розмовляє мовою математики; букви цієї мови – круги, трикутники та інші математичні фігури.   Галілео Галілей

 

І. Організаційний момент. Вітання з класом.

Вчитель. На сьогоднішньому уроці в нашому класі присутні гості. Ми раді їх вітати та запрошуємо до співпраці.

 

ІІ. Мотивація навчальної діяльності учнів.

На сьогоднішньому уроці нам необхідно добре попрацювати, щоб повторити та систематизувати наші знання про рівнобедрений трикутник. Тож я бажаю вам успіху! (Слайд №2-7)

 

ІІІ. Повідомлення теми, мети та завдань уроку.

На сьогоднішньому уроці ми повторимо теоретичні відомості про рівнобедрений трикутник, застосовуватимемо наші знання для розв’язування задач різного рівня складності, ознайомимося з результатами роботи над проектом.

Сьогодні оцінювання своєї праці ви проводитимете самостійно - заповнюючи картки самооцінювання після кожного етапу уроку. Я сподіваюсь на вашу чесність та об’єктивність. (Учитель роздає картки для самооцінювання).

 

IV. Перевірка домашнього завдання.

Про стан виконання домашнього завдання доповідає учень консультант.

 

V. Актуалізація опорних знань учнів. (Слайд №8)

 

1) Усне опитування проводить учень консультант з використанням трикутників з планіметричного набору фігур.

• Що називають трикутником?
• Які існують види трикутників?
• Продемонструйте: рівносторонній, різносторонній, рівнобедрений трикутники.
• Продемонструйте: гострокутний, тупокутний, прямокутний трикутники.
• Який трикутник називається рівнобедреним?  Продемонструйте.
• Як називаються сторони рівнобедреного трикутника?
• Які властивості має рівнобедрений трикутник?
• Сформулюйте ознаки рівнобедреного трикутника.

Вчитель. Оцініть свою роботу на даному етапі уроку і поставте у картку самооцінювання відповідний бал.

 

2) Представлення результатів роботи над проектом «Рівнобедрений трикутник. Історія вивчення та практичне застосування».

Для роботи над вказаним проектом усі учні класу поділені на дві групи – «Науковці» та «Дослідники». «Науковці» опрацьовували літературу з історії математики та інші додаткові джерела і з’ясовували історію вивчення рівнобедреного трикутника. «Дослідники» вивчали, яким чином дана фігура використовується людиною в повсякденному житті.

Представники груп доповідають про свої результати. (Слайд №10-13, слайд №14-24).

 

VІ. Розв’язування задач. (За роботу на кожному етапі уроку учні виставляють відповідний бал в картку самооцінювання)

 

1)Усні  задачі за готовими малюнками.(дошка, слайд №26-29)

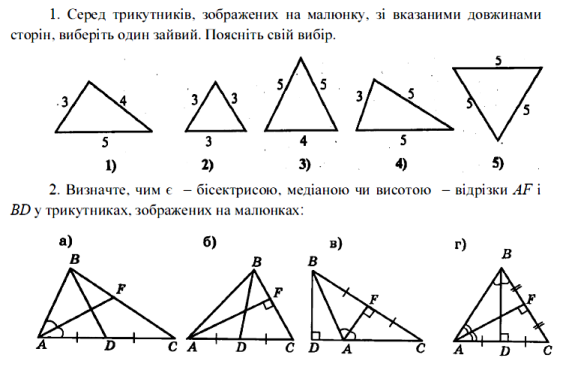
3. На основі поданих малюнків трикутників (слайд ) перевірити, чи правильно обчислені вказані величини:

 

 

 

  

 

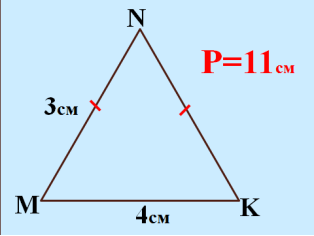
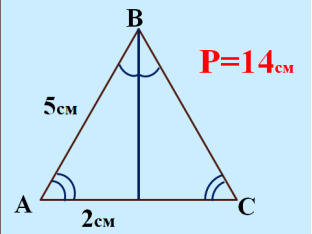
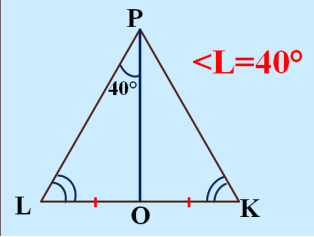
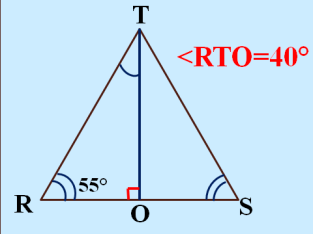
2) Робота в парах з завданнями на встановлення відповідності.

Установіть відповідність між кутом (1 – 4) і його величиною ( А – Д). За кожну відповідь 0,5 бала.
1	Другий гострий кут прямокутного трикутника, якщо перший дорівнює 320.	А	600
2	Третій кут трикутника, якщо два його кути дорівнюють 250 і 600	Б	950
3	Кут при основі рівнобедреного трикутника, якщо кут при вершині дорівнює 500.	В	580
4	Гострий кут рівнобедреного прямокутного трикутника.	Г	650
		Д	450

 

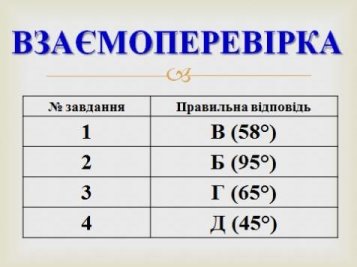
Учні обмінюються зошитами і проводять взаємоперевірку на основі вказаних на екрані правильних відповідей, (Слайд №31)отриманий результат заносять в картку самооцінювання.

3)Хвилинка відпочинку. Гра «Вірю – не вірю». (Слайд №32-40)

Чи віриш що …

1)…Піфагор був учасником 58 Олімпійських ігор? (Так)

2)…існує геометрія, у якій паралельні прямі перетинаються? (Так)

3)…Л.М.Толстой порівнював людину зі звичайним дробом? (Так)

4)…квадрат дав назву відомому танцю кадриль? (Так)

5) …вивченню властивостей трикутника присвятив свої дослідження Наполеон? (Так)

6)… число 1001 є простим? (Ні)

7)… Фалес був уболівальником і помер на трибуні Олімпійського стадіону під час бою Піфагора? (Так)

8)… Професор математики Оксфордського університету Чарльз Людовік Доджсон (1832 – 1898), видав під іменем Льюїса Керролла дитячі книжки «Аліса в країні чудес», «Аліса в Задзеркаллі»

 

4) Робота з підручником. Коментоване розв’язування задачі №238 (ст.85) з попереднім колективним структурним аналізом умови задачі.

 

5) Тестування.

 

1. Як називається трикутник, у якого дві сторони рівні?

А. Різносторонній.  

Б. Прямокутний.           

В. Рівнобедрений.           

Г. Рівносторонній.   

Д. Інша відповідь.

2. Як називається трикутник, у якого всі сторони різні?

А. Різносторонній.   

Б. Прямокутний.   

В. Рівнобедрений.      

Г. Рівносторонній.

Д. Інша відповідь.

3. Як називається трикутник,  у якого всі сторони рівні?

А. Різносторонній.    

Б. Прямокутний.     

В. Рівнобедрений.      

Г. Рівносторонній.

Д. Інша відповідь.

4. Які кути у рівнобедреному трикутнику рівні?

А. Кути при основі.              

Б. Всі рівні.         

В. Всі різні.     

Г. Внутрішній і зовнішній при одній вершині.    

Д. Інша відповідь.

5. Чим є бісектриса рівнобедреного трикутника, проведена до основи?

А. Тільки бісектрисою.             

Б. Медіаною.           

В. Висотою.        

Г. Медіаною і висотою.

Д. Інша відповідь.

6. Кут при вершині рівнобедреного трикутника дорівнює 120⁰. Знайдіть кут при основі.

А. 60⁰.            Б. 30⁰.           В. 120⁰.         Г. 20⁰.          Д. Інша відповідь.

7. Знайдіть периметр рівнобедреного трикутника, якщо основа 12 см, а бічна сторона 8 см.

А. 20 см.        Б. 33  см.         В. 29 см.         Г. 28 см.        Д. Інша відповідь.

8. Чому дорівнює внутрішній кут рівностороннього трикутника?

А. 120⁰.          Б. 30⁰.               В. 90⁰.               Г. 60⁰.              Д. Інша відповідь.

9. Периметр рівнобедреного трикутника дорівнює 100см. Знайдіть його сторони, якщо вони пропорційні числам 1, 2, 2.

А. 20, 40, 40.       Б. 40, 20, 20.      В. 60, 20, 20.    Г. 20, 30, 50.   Д. Інша відповідь.

10. Знайдіть кути рівнобедреного трикутника, якщо сума двох з них дорівнює 80⁰.

А. 40⁰, 40⁰, 80⁰.      Б. 40⁰, 40⁰, 100⁰.    В. 80⁰, 80⁰, 20⁰.     Г. 20⁰, 60⁰, 100⁰.

Д. Інша відповідь.

11. Знайдіть периметр рівнобедреного трикутника з основою а і бічною стороною в.

А. а + в.           Б. 2а + в.            В. а + 2в.             Г. а* в.            Д. Інша відповідь.

12. Кут при вершині рівнобедреного трикутника дорівнює 40⁰. Знайдіть кут при основі.

А. 70⁰.                 Б. 40⁰.               В. 100⁰.            Г. 140⁰.             Д. Інша відповідь.

 

VІІ. Підсумок уроку – проводиться колективно за схемою:

На сьогоднішньому уроці

• повторили…
• з’ясували…
• розв’язали…
• дізналися…
• досягли…

Рефлексія (створення ситуації успіху)

Вчитель.  Усіх результатів ми змогли досягнути завдяки активній праці. Існує така легенда:

У середні віки у французькому місті Шарті будували собор. Якось трьох тачечників, які виконували однакову роботу - перевозили камінь, запитали:

- Слухайте, друзі, що ви робите?

Перший робітник похмуро глянув і роздратовано відповів: „Не бачиш – камінь тягаю на майданчик, хай йому ґрець!”

Другий спокійно сказав: „ Що я роблю? Заробляю на кусень хліба для своєї родини.”

А третій розігнувся, витер спітніле чоло, усміхнувся і з гордістю сказав: „ Я будую Шартський собор!”

         Ідея цієї притчі актуальна й нині: праця не лише нестерпний тягар чи засіб для матеріального забезпечення, а й – найперше – джерело творчості й шлях для досягнення успіху.

• Діти, я переконана, що ми з вами завдяки нашій активній праці досягли неабиякого успіху!!!

VІІІ. Оцінювання роботи учнів на уроці.

Окремо оцінюється робота учня консультанта та учнів, які доповідали по проекту. Оцінювання решти учні проводить після перевірки тестів з врахуванням карток самооцінювання.

ІХ. Повідомлення диференційованого домашнього завдання. (Слайд №42)

Психологічне діагностування .

«Результат справ часто залежить від дрібниць» (Тіт Лівій)

Пропонується учням вибрати фігуру на свій смак: коло, квадрат, трикутник, прямокутник, ламана.

Коло – доброзичливі, піклуються про інших, але дещо не рішучі, балакучі, мають широке коло друзів.

Квадрат – мають охайний, підтягнутий вигляд, робоче місце впорядковане, працелюбні, дотримуються правил та інструкцій.

Трикутник – мають модний зовнішній вигляд, прагнуть до лідерства, влади, нетерплячі, люблять розваги.

Прямокутник – всім цікавляться, уникають конфліктів, схильні до втрати речей, весь час знаходять нових друзів.

Ламана – прагнуть до знань, але робоче місце в безладі, не люблять паперової роботи, дотепні.