Розв'язування задач підвищеної складності з теми «Елементи прикладної математики»

Про матеріал

Узагальнення відомостей про прикладні задачі, алгоритм розв'язування прикладних задач; формування вмінь побудови математичної моделі та розв'язування прикладних задач.

Перегляд файлу

Алгебра. 9 клас

Тема уроку. Розв'язування задач підвищеної складності з теми «Елементи прикладної математики»

Мета уроку. Узагальнення відомостей про прикладні задачі, алгоритм розв'язування прикладних задач; формування вмінь побудови математичної моделі та розв'язування прикладних задач.

Формування компетентностей:

✵ предметна компетентність: формувати вміння застосовувати набуті знання в нестандартних ситуаціях, розв'язувати задачі підвищеної складності;

✵ ключові компетентності:

✵ спілкування державною мовою — розуміти, пояснювати і перетворювати тексти математичних задач (усно і письмово);

✵ уміння вчитися впродовж життя — визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети, доводити правильність власного судження або визнавати помилковість.

Тип уроку: застосування знань і вмінь.

Обладнання та наочність: опорні таблиці та схеми

Хід уроку

І. Організаційний етап

ІІ. Актуалізація опорних знань

Фронтальне опитування

Які задачі називають прикладними?
Сформулювати послідовність дій для розв'язування прикладних задач за допомогою рівнянь та систем рівнянь.
Опорна таблиця: що таке відсотки

ІІІ. Формулювання теми, мети, завдань уроку; мотивація навчальної діяльності.

Сьогодні ми відпрацюємо вміння розв'язувати прикладні задачі підвищеної складності з теми «Елементи прикладної математики». Основну увагу слід приділити методам їх розв'язування.

ІV. Застосування знань і вмінь

Задача 1.

У першому сплаві золото і срібло знаходяться у відношенні 2:3, а у другому – 3:7. На скільки грамів одного зі сплавів треба взяти більше, щоб одержати 8г нового сплаву, в якому золото і срібло знаходяться у відношенні 5:11?

Розв’язання

Нехай х г – маса частини першого сплаву, у г – маса частини другого сплаву.

Концентрація золота в першому сплаві дорівнює 0,4, а концентрація золота в другому сплаві дорівнює 0,3. Концентрація золота в остаточному сплаві дорівнює .

	Маса (г)	Золото
	Маса (г)	Концентрація (у частинах)	Маса (г)
І сплав	х	0,4	0,4х
ІІ сплав	у	0,3	0,3х
Остаточний сплав	х+у=8		2,5

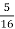від 8 становить 2,5 (г);
Розвязавши утворену систему, знаходимо: х=1; у=7.
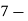1=6.

на 6 г.

Задача 2.

Два сплави складаються з цинку, міді й олова. Відомо, що перший сплав вміщує 40% олова, а другий 26% міді. Відсотковий вміст цинку в першому і другому сплавах однаковий. Сплавивши 150 кг першого сплаву і 250 кг другого, дістали новий сплав, що містить 30% цинку. Скільки олова вміщує цей новий сплав?

Розв’язання

	Вміст у першому сплаві (%)	Вміст у другому сплаві (%)	Вміст у третьому сплаві (%)	Маса у третьому сплаві (кг)
Олово	40	100-26-60+х=х+14		60+2,5(х+14)
Мідь	Х	26		65+1,5х
Цинк	100-(40+х)=60-х	60-х	30	120

150+250=400(кг)- маса третього сплаву;
30% від 400 кг становить 120 кг – маса цинку в третьому сплаві;
40% від 150 кг становить 60 кг – олова відійшло з першого сплаву до третього;
(х+14)% від 250 кг становить 2,5(х+14) (кг) олова відійшло з другого сплаву до третього;
Х% від 150 кг становить 1,5х (кг) міді відійшло з першого сплаву до третього;
26% від 250 кг становить 65 кг міді відійшло з другого сплаву до третього;
60+2,5(х+14)+65+1,5х=280;

60+2,5х+35+65+1,5х=280;

4х=120;

Х=30.

60+2,5(х+14) =60+2,5(30+14) = 170 (кг).

Відповідь: 170 кг.

Задача 3.

Бджоли, переробляючи квітковий нектар на мед, звільняють його від значної частини води. Дослідження показали, що нектар зазвичай вміщує близько 70% води, а вироблений з нього мед вміщує тільки 17% води. Скільки кілограмів нектару доведеться переробити бджолам, щоб дістати 1 кг меду?

Розв’язання

Внаслідок переробки бджолами квіткового нектару утворюються мед і вода.

	Маса (кг)	Вміст води
	Маса (кг)	%	кг
Нектар	у	70	0,7у
Мед	1	17	0.17
Вода	х	100	х

70% від у становить становить 0,7у (кг);
17% від 1 кг становить 0,17 1=0,17 (кг);
100% від х становить 1 х=х (кг).

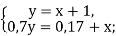
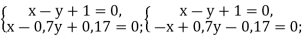
у2,77.

Відповідь:

Задача 4.

Із молока, жирність якого становить 5%, виготовляють сир жирністю 15,5%. При цьому залишається сироватка жирністю 0,5%. Скільки сиру виходить із 1 тонни молока?

Розв’язання

	Маса (кг)	Жир
	Маса (кг)	Вміст (%)	Маса (кг)
Молоко	1000	5	50
Сир	х	15,5	0,155х
Сироватка	1000-х	0,5	0,005(1000-х)

Нехай х кг сиру виходить з 1т (1000 кг) молока.

5% від 1000 кг становить 0,05 1000=50 (кг) – маса жиру в 1 т молока;
15,5% від х становить 0, 155(1000-х) (кг) – маса жиру в х кг сиру;
0,5% від (1000-х) кг становить 0,005(1000-х) (кг) – маса жиру в (1000-х) (кг) сироватки.

Оскільки при переробці молока кінцевими продуктами є сир та сироватка, то маса жиру в молоці дорівнює сумі мас жиру в сирі та сироватці.

Складаємо рівняння:

0,155х+0,005(1000-х)=50;

0,155х+5-0,005х=50;

0,15х=45; х=45:0,15; х=300.

Відповідь:300 кг.

Задача 5.

Скільки води треба долити до 60 кг 20% розчину соляної кислоти, щоб отримати 15% розчин?

Розв’язання

І спосіб

Нехай х кг води треба долити до розчину.

	Маса (кг)	Соляна кислота
	Маса (кг)	Вміст (%)	Маса (кг)
І розчин	60	20	12
ІІ розчин	60+х	15	0,15(60+х)=12

Якщо до першого розчину долити х кг води, то концентрація соляної кислоти в утвореному розчині зменшиться, а її маса залишиться незмінною.

Розв’язавши рівняння, одержимо х=20.

Відповідь: 20 кг води.

ІІ спосіб

Оскільки вода має концентрацію 0%, то:

15= ;

15(60+х)=1200;

Х=20.

Відповідь: 20 кг води.

Задача 6.

Заробітну платню збільшили на 20%, а ціни на продукти зменшили на 15%. На скільки відсотків робітник тепер на свою зарплатню зможе купити більше продуктів, ніж раніше?