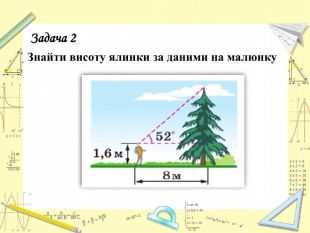
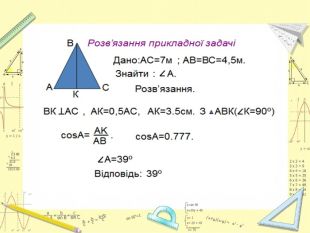
Розв’язування задач прикладного та практичного направлення

Розв’язування задач прикладного та практичного направлення Світ, що нас оточує, - це світ геометрії. Тож давайте його пізнавати! Піфагор

Мета: Узагальнити, систематизувати та закріпити знання учнів по темі «Розв’язування прямокутних трикутників»;продовжити формувати вміння будувати математичні моделі при розв’язуванні задач практичного змісту;розвивати пізнавальний інтерес учнів;формувати навички роботи в групі, виховувати почуття взаємодопомоги, взаємопідтримки;

Тематичний кросворд. ПРЯМОКТНИЙУГІПОТЕНУЗАПІФАГОРІЙЦІДВАЄГИПЕТСЬКИЙПРОЕКЦІЯГРАДУСppt_cppt_cppt_cppt_cppt_cppt_cppt_c

«Західний експрес»

Перша станція

Дідорук Д. Янчук Д. Марценюк А. Сас О. Ругаєва К. Багін Д. Борейко А. Група Теоретиків

Задача1 Визначте на якій глибині розташована лінія метро, якщо кут нахилу ескалатора становить 30°, а відстань між світильниками 5м?

30°АСВДано: АВС прямокутний∠А=30°, AD=DB, AD=5 м,Знайти: BC-? DРозв’язання. AD=DB, AB=2 AD=2·5=10 (м) АВС прямокутний, за означенням синуса гострого кута прямокутного трикутника sin∠А=ВСАВ ⟹ ВС= АВsin∠А,ВС= 10 sin 30°=10∙12=5(м)Відповідь: глибина лінії метро 5 м  

«Чи правильно що…»

1. Чи правильно, що теорема в перекладі з грецької мови означає ”вистава” ? 2. Чи правильно, що катетом називали висоту прямокутного трикутника ?3. Чи правильно, що cos 40 о < sin 70 о ? 4. Чи правильно, що центр кола, описаного навколо прямокутного трикутника є серединою гіпотенузи? 5. Чи правильно, що tg 90о не існує? 6. Чи правильно, що sin 25о < cos 50 о ? 7. Чи правильно, що sin 75о < sin 50 о ? 8. Чи правильно, що sin2 В + cos2 В = 1? 9. Чи правильно що ,відношення прилеглого до кута катета до гіпотенузи в прямокутному трикутнику називають косинусом кута.10. Чи вірите ви, що будь-який прямокутний трикутник називається єгипетським;

Відповіді{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}12345678910тактактактактактакнітактакні

Зупинка «Історична»

Група Істориків. Паламарчук ОКозьолок Ю. Тиран Я. Ковальчук Д. Дунець Д. Музичук О. Ровінець В. Живулін В.

Єгипетський трикутник 32+42=52

  Частина папірусу Ахмеса

  Папірус з Оксиринха

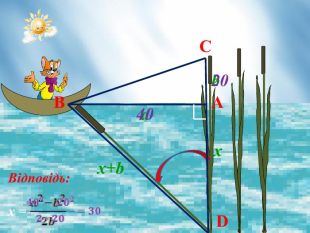
Задача індійського математика. ХІІ століття Бхаскари: На березі річки росла самотня тополя. Раптом налетівші вітри зламали її стовбур. Бідна тополя впала, утворивши кут між стовбуром і поверхнею води річки. Запам'ятай тепер, що в цьому місці річка. У чотири лише фута була шириною. Верхівка зламалася, залишивши всього три фути від усього стовбура. Прошу тебе, швидше мені скажи Яка висота тополі?»

 Задача 2 Знайти висоту ялинки за даними на малюнку

Дано: АЕ=1,6м; DE= 8м; ∠ВАС=52°; АЕ⊥𝐷𝐸; ВD⊥DE;Знайти: BD -?Розв’язанння: АВСDE52°81,6 ACDE прямокутник, АЕ=СD= 1,6м; АС=ED= 8м;∆ ACB прямокутний, ∠С=90°, ∠ВАС=52°, АС=8 м tg∠ВАС=ВСАС; ВС=АС· tg∠ВАС;  ВС= 8·1,279≈10,2 (м)3)ВD=DC+BC=10,2+1,6=11,8 (м)Відповідь : висота ялинки 11,8 м 

Фізкультхвилинка для очей

Зупинка «Юних дослідників»

Група «Юних дослідників»Ястремська Д. Юськова А. Скримська А. Ковальський К. Карбовська А. Остапчук Д. Продан О. Слободзяний В.

Один із методів доведення теореми Піфагора. Площа квадрата побудованого на гіпотенузі прямокутного трикутника дорівнює сумі площ квадратів побудованих на катетах.

Задачі з використанням прямокутного трикутника 1. Драбину довжиною 13 м., приставили до стіни так, що відстань до нижнього кінця драбини до стіни 5 м. На якій висоті від землі знаходиться кінець драбини? Розв’язання: ∆АСВ прямокутний, АВ =13м, ВС= 5м, за теоремою Піфагора АС2=АВ2-ВС2, АС=132−52= 144 =12(м) 

Задачі з використанням прямокутного трикутника 2. DABCРозв’язання:∆DCВ прямокутний, tg ∠𝐵𝐷𝐶= 𝐵𝐶𝐷𝐶;  DC=𝐵𝐶𝑡𝑔∠𝐵𝐷𝐶 = 80𝑡𝑔 30° = 8033 =138,72 (м)∆АСD прямокутний, tg ∠𝐴𝐷𝐶 = 𝐴𝐶𝐷𝐶 ; AC = DC · tg ∠𝐴𝐷𝐶 = 138,72 · tg 65° = = 138,72·2,144=297,4 5(м ) Відповідь: висота літака 297, 45 м 

Задачі з використанням прямокутного трикутника 3. Ширина будинку 7 м, довжина крокви 4,5 м. Під яким кутом крокви нахилені до стелі ?

Задача 3 Знайдіть кут відхилення Пізанської вежі, якщо її висота 55 м, а тінь о півдні становить 5.3 м?АСВРозв’язання:∆АВС прямокутний,∠С=90°ВС=55м, АС = 5,3мtg ∠СВА=А𝐶В𝐶 ; tg ∠СВА=5,355=0,096;∠СВА=5,5°;   Відповідь: 5,5°

Станція «Геодезистів»

Група «Геодезистів»Вараниця І. Берлінська Е. Гіпко К. Меркулов О. Пастушок Д. Годований П. Боднар О. Святецький А.

Задачі з використанням прямокутного трикутника 1)Телеграфний стовп висотою 14 м знаходиться на березі річки. Верхній кінець стовпа видно з іншого берега під кутом 22 ° до горизонталі. Знайдіть ширину річки. АСВ22°14 Розв’язання:∆АСВ прямокутний,∠С=90°, ∠А=22°tg∠ A= 𝐵𝐶𝐴𝐶;AC= 𝐵𝐶𝑡𝑔∠𝐴=14𝑡𝑔 22==140,404= 34,65 (м) 

Задачі з використанням прямокутного трикутника 2. Ви пливете в човні по озеру і хочете дізнатись його глибину. Чи можливо для цього скористатися очеретом, що виглядає із води, не вириваючи його?

BАCDbaxx+b. Відповідь:x =4020

3. Переріз залізничного насипу має форму рівнобічної трапеції . Нижня основа трапеції дорівнює 10 м, висота насипу - 2 м, а його укіс - 35°. Знайдіть ширину верхньої частини насипу (верхню основу трапеції).

Дано: ABCD –рівнобічна трапеція,АD=10м, BQ= 2м -висота, ∠BAQ=35°Знайти: ВС-? АВСDQРозв’язання. ABCD –рівнобічна трапеція , AB=CD, ∠BAQ= ∠ CDA =35°, висота BQ=2 м 2) ∆AQB – прямокутний, ∠Q=90°, tg ∠A=𝑩𝑸𝑨𝑸; ⟹AQ=𝑩𝑸tg ∠A = 𝟐𝒕𝒈𝟑𝟓°=𝟐𝟎,𝟕≈ 2,9 (м)3)За властивістю рівнобічної трапеції AQ=𝑨𝑫−𝑩𝑪𝟐 ⟹BC=AD-2 AQ=10-2·2,9=10-5,8=4,2 (м) Відповідь: ВС=4,2м  35°2

Задача 4. На вершині гори відбувся вибух. Звук вибуху почули у підошви гори в точці К через 4 с після вибуху. Знайдіть висоту гори, якщо з точки її вершину видно під кутом 30° , а швидкість звуку 331 м / с.

Дано: ∠АКО=30°,t=4c, 𝜐=331м/с. Знайти: h=АО-?Розв’язання: ∆AOK прямокутний, ∠О=90°,АК =S = t𝜐= 4·331=1324(м)Sin ∠𝐾= 𝐴𝑂𝐴𝐾 ⇒AO= AK · Sin ∠𝐾,h= AO = 1324 · Sin 30° =1324 · 0,5= 662(м)Відповідь: висота гори 662 м 

Весела хвилинка. Співаю я хвалу довірі,Проте і перевірка - не обуза. В одній вершині на кутіСтрічались Катет і Гіпотенуза. У Катета вона була одна. Гіпотенузу він кохав, не вірив він пліткам. А в час оцей на куті сусіднім. З іншим Катетом стрічалася вона.І діло це закінчилося конфузом. От після цього й вір Гіпотенузам!

Гра «Математичне лото»І варіантІІ варіант

Домашнє завдання. Повторити § 16, 17,18№626, 628