Розв’язування задач прикладного та практичного направлення
Тема уроку. Розв’язування прямокутних трикутників
Мета уроку. Узагальнення, систематизація та закріплення знань про теорему Піфагора, розв’язування прямокутних трикутників; застосування набутих знань і вмінь у практичній діяльності.
Розвиток вмінь аналізувати, робити висновки, знаходити власні способи розв’язання.
Формування компетентностей: соціальних (розвиток пізнавальної активності учнів, робота в команді, усвідомлення власного внеску в спільну роботу, вміння брати відповідальність), комунікативних (формування власної точки зору, розвиток культури мовлення, вміння доводити власну позицію). Виховування активності, уваги, кмітливісті, самостійністі.
Прищеплення інтересу до математики.
Тип уроку. Урок подорож, узагальнення і систематизації знань
Світ, що нас оточує, - це світ геометрії. Т Тож давайте його пізнавати!
Піфагор
І. Організаційна частина
ІІ. Повідомлення теми і мети уроку
Сьогодні ми проведемо підсумковий урок з теми „ Розв’язування прямокутних трикутників ”.
ІІІ. Актуалізація опорних знань
Повторимо матеріал, вивчений на уроках.
Розгадаємо кросворд
- Як називається трикутник в якому є прямий кут?
- Як називаються сторони прямокутного трикутника, що лежить проти кута 90?
- Як називали учнів піфагора?
- Скільки елементів має бути відомо щоб можна було розв’язати прямокутний трикутник?
- Трикутник зі сторонами 6,8,10 називається?
- Відрізок що сполучає основу перпендикуляра та основу похилої називається?
- В яких одиницях вимірюються кути?
Проведемо подорож. Наша гра математична.
Клас було поділено на групи, кожна з яких отримала завдання з міні проектів
Можливо, сьогодні, ви щось дізнаєтесь і нове.
Знайомтеся з капітанами груп: 1.
2.
3.
4.
Будьте уважні , працюйте та бали збирайте ,а капітани їх гарно рахують та у таблицю всіх їх вносять!
Розпочнемо подорож

Розпочнемо нашу подорож з першої станції Метрополітен
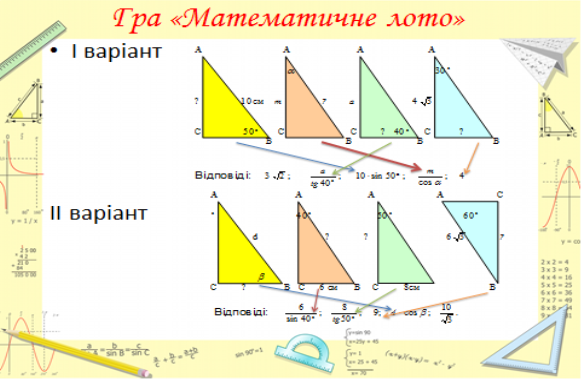
Група «Теоретиків»
Ми група теоретики! Теорію трикутників будемо вивчати, щоб легко було задачі про них розв`язати.
Завдання , яке було поставлене перед нами систематизувати теоретичний матеріал з теми «Прямокутні трикутники» і результат своєї роботи подати у вигляді бюлетня
У ході виступу групи учні склали таблиці класифікації розв’язання прямокутних трикутників.


Задача1
Визначте на якій глибині розташована лінія метро, якщо кут нахилу ескалатора становить 30°, а відстань між світильниками 5м?
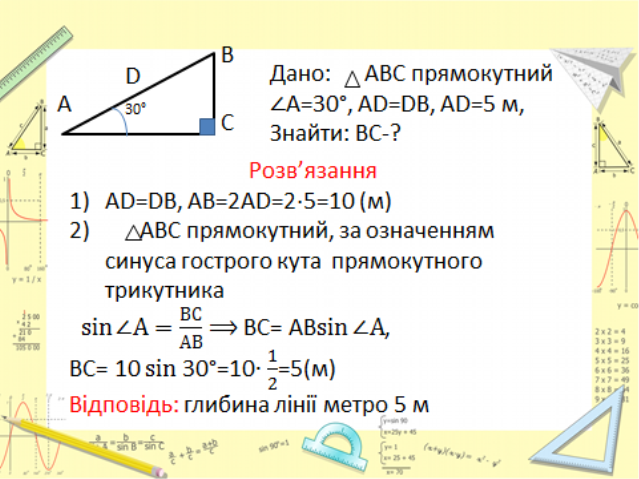
.
Переходимо до наступного конкурсу ”Чи правильно що...”
Залишається відповісти: „так” чи „ні”
Запитання
- 1. Чи правильно, що теорема в перекладі з грецької мови означає ”вистава” ? (так)
- 2. Чи правильно, що катетом називали висоту прямокутного трикутника ? (так, в середні віка, інші сторони – гіпотенуза і основа)
- 3. Чи правильно, що cos 40 о < sin 70 о ? (так)
- 4. Чи правильно, що центр кола, описаного навколо прямокутного трикутника є серединою гіпотенузи? (так)
- 5. Чи правильно, що tg 90о не існує? (так)
- 6. Чи правильно, що sin 25о < cos 50 о ? (так)
- 7. Чи правильно, що sin 75о < sin 50 о ? (ні)
- 8. Чи правильно, що sin2В + cos2В = 1? (так)
- 9. Чи правильно ,відношення прилеглого до кута катета до гіпотенузи в прямокутному трикутнику називають косинусом кута.
- 10. Чи вірите ви, що будь-який прямокутний трикутник нази¬вається єгипетським; (Ні.)
Друга зупинка «Історична»
Ще в давнину людство дізналось про властивості прямокутного трикутника - як одну з перших геометричних фігур. Ім’я відомого математика складається з трьох складів: перший склад – число, другий – нота, третій – одне з імен давньоєгипетського бога Сонця, це Пі-фа-гор, Народився Піфагор близько 570 року до нашої ери в Сидоні Фінікійському в родині тіровского багатого купця. Завдяки фінансовому стану своїх батьків, юнак зустрічався з багатьма мудрецями тієї епохи і ввібрав в себе їх знання як губка. Ще з часів подорожі Піфагора по Єгипту йому був відомий єгипетський трикутник зі сторонами 3,4,5. Піфагор провів 22 роки в Єгипті займаючись спостереженнями зоряного неба і геометрією, осягнувши глибоко знання єгиптян довів свою теорему і в подяку богам велів зажарити 100 биків.
в якій квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів. Піфагор був олімпійським чемпіоном з кулачного бою на олімпіаді в 548 р. до н.е.
![]() А ще вчені Індії зводили розв’язування будь-яких трикутників до розв’язання прямокутних трикутників. Такі задачі можна знайти у давньоєгипетських папірусах, старовинних індійських книгах. У папірусах Ахмеса згадується про властивості рівнобедреного та прямокутного трикутників, датованими вавилоняни 4000 років тому. Систематизував ці відомості Евклід у першому трактаті з геометрії «Началах».
А ще вчені Індії зводили розв’язування будь-яких трикутників до розв’язання прямокутних трикутників. Такі задачі можна знайти у давньоєгипетських папірусах, старовинних індійських книгах. У папірусах Ахмеса згадується про властивості рівнобедреного та прямокутного трикутників, датованими вавилоняни 4000 років тому. Систематизував ці відомості Евклід у першому трактаті з геометрії «Началах».

![]()


![]()
![]()
![]()
Єгипетський трикутник

 32+42=52
32+42=52
Отож пропонуємо вашій увазі задачу індійського математика XII століття Бхаскарі

«На березі річки росла самотня тополя.
Раптом налетівші вітри зламали її
стовбур.
Бідна тополя впала, утворивши кут між
стовбуром і поверхнею води річки.
Запам'ятай тепер, що в цьому місці річка
У чотири лише фута була шириною.
Верхівка зламалася, залишивши всього
три фути від усього стовбура.
Прошу тебе, швидше мені скажи:
Яка висота тополі?»
Використовуємо єгипетський трикутник, висота зламаної частини 5 футів. Отож висота тополі 3+5 =8 футів.
Продовжуємо нашу подорож через мальовничі Карпати,де перед нами відкривається краєвид карпа
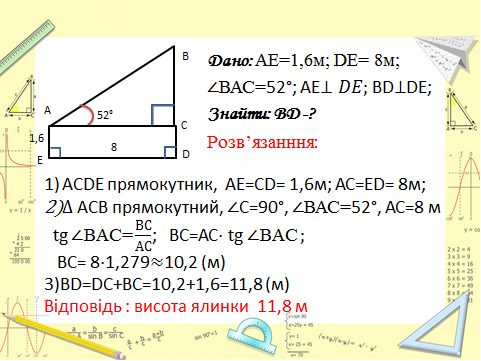
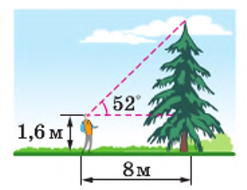 Задача 2
Задача 2
Знайти висоту ялинки
тських лісів.
Фізкультхвилинка ДЛ Я ОЧЕЙ
Третя зупинка «Юні дослідники»
Ми група «Юні дослідники».
Наша група працювала над везізом: «Найдосконаліший мозок іржаві без дії»
Ми досліджували методи доведення теореми Піфагора, та один із них пропонуємо Вам
![]()

![]()

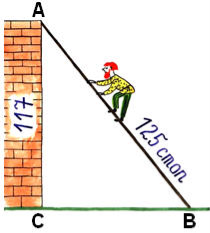
Також ми досліджували де застосувуются прямокутні трикутники.
Розглянемо кілька прикладів.
- Драбину довжиною 13 м., приставили до стіни так, що відстань до нижнього кінця драбини до стіни 5 м. На якій висоті від землі знаходиться кінець драбини?
-
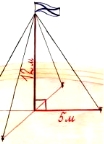 Для закріплення щогли потрібно встановити 4 троси. Один кінець кожного троса повинен прикріплюватися на висоті 12 м, другий на землі на відстані 5 метрів від щогли. Чи досить 50м тросу для закріплення щогли?
Для закріплення щогли потрібно встановити 4 троси. Один кінець кожного троса повинен прикріплюватися на висоті 12 м, другий на землі на відстані 5 метрів від щогли. Чи досить 50м тросу для закріплення щогли?

Задача 3
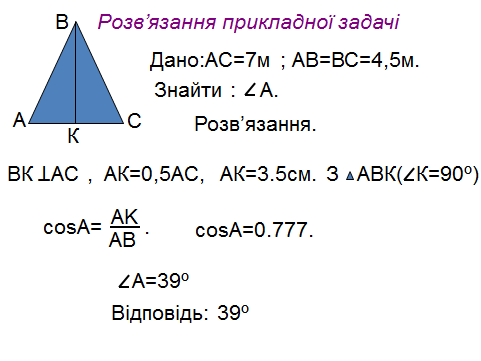
![MMj02951830000[1]](/uploads/files/1804387/334541/375761_html/images/334541 26.png) Ширина будинку 7 м, довжина крокви 4,5 м.
Ширина будинку 7 м, довжина крокви 4,5 м.
Під яким кутом крокви нахилені
до стелі ?
Задача 3 Самостійно з перевіркою
знайдіть кут нахилу Пізанської вежі, якщо її висота 56 м, а тінь о півдні становить 5.3 м?

.
![]() ІV. Наступна наша станція « геодезистів»
ІV. Наступна наша станція « геодезистів»
Є професії, пов’язанні з частим розв’язуванням трикутників. Насамперед цим займаються геодезисти. Коли ж на основі їх матеріалів у проектних організаціях опрацюють проект, геодезисти знову міряють кути, розв’язують трикутники, забивають кілочки – «прив’язують» опрацьований проект до місцевості.
А навіщо вони розв’язують трикутники? Щоб визначити потрібні відстані, не виміряючи їх безпосередньо. Є ще спеціалісти, які розв’язують подібні задачі в шахтах, тунелях, метро та інших підземних розробках.
- Отож давайте розглянемо деякі з задач
- 1)Телеграфний стовп висотою 14 м знаходиться на березі річки. Верхній кінець стовпа видно з іншого берега під кутом 22 ° до горизонталі. Знайдіть ширину річки.
- Рішення.
У ▲ CAB tg α = CB / AC, звідки ширина річки AB = CB / tg α ≈ 35 m
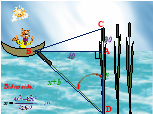
2)Ви пливете в човні по озеру і хочете дізнатись його глибину. Чи можливо для цього скористатися очеретом, що виглядає із води, не вириваючи його?
Розв’язування.
Злегка відхиливши очерет і тримаючи його в натягнутому стані, заміряємо відстань а між точками А і В, в яких очерет перетинає поверхню води відповідно у вертикальному і нахиленому положенні. Повернемо очерет в початковий стан і визначимо висоту b над водою, на яку підніметься при цьому точка В нахиленого очерету, зайнявши початкове положення С. Тоді, позначивши через D основу очерету, а через х - шукану глибину АD, з прямокутного трикутника АВD знаходимо невідомі сторони за теоремою Піфагора,
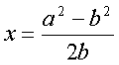 звідки і
звідки і
Задача 3 Переріз залізничного насипу має форму рівнобічної трапеції (мал. 204). Нижня основа трапеції дорівнює 10 м, висота насипу - 2 м, а його укіс - 35°. Знайдіть ширину верхньої частини насипу (верхню основу трапеції).

Задача 5
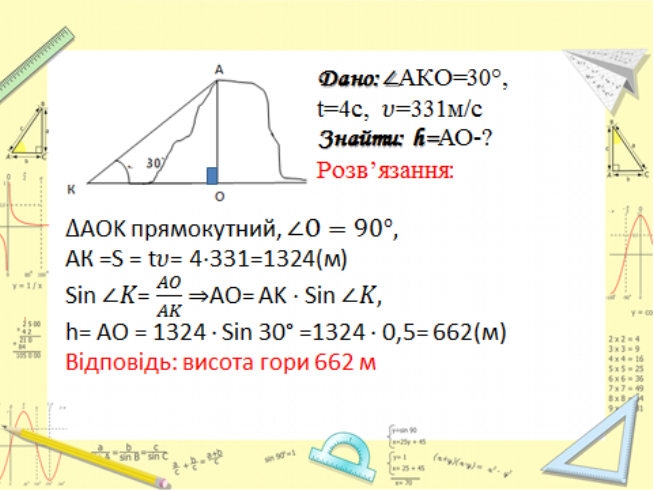
На вершині гори здійснив вибух. Звук вибуху почули у підошви гори в точці К через 4 с після вибуху. Знайдіть висоту гори, якщо з точки До її вершина видно під кутом 30 `, а швидкість звуку 331 м / с.
![]()
![]()
![]()
Вихідна рефлексія.
1. Що сьогодні на уроці було найважливішим ?
2. Що на уроці було цікавим ?
3. Що викликало ускладнення, труднощі?
4. Над чим слід попрацювати вдома.
Вчитель. Зробимо підсумок нашої проектної діяльності. У проекті було використано різноманітні задачі практичного змісту. У процесі роботи над проектом ви спостерігали застосування ваших знань для розв’язання проблем прикладного характеру. Сьогодні ми довели собі, що без математики неможлива успішна діяльність людини.
Домашнє завдання .
Весела хвилинка.
 Співаю я хвалу довірі,
Співаю я хвалу довірі,
Проте і перевірка - не обуза.
В одній вершині на куті
Стрічались Катет і Гіпотенуза.
У Катета вона була одна.
Гіпотенузу він кохав, не вірив він пліткам.
А в час оцей на куті сусіднім
З іншим Катетом стрічалася вона.
І діло це закінчилося конфузом.
От після цього й вір Гіпотенузам!


про публікацію авторської розробки
Додати розробку
