Розв'язування задач з тригонометричними функціями
Тема. Розв'язування задач з тригонометричними функціями
Мета: узагальнити та систематизувати знання учнів про означення тригонометричних функцій гострого кута, їх основні властивості, тригонометричні тотожності, а також про способи застосування набутих знань під час виконання вправ.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: конспект 21.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Розв'язання завдань домашньої роботи перевіряється за зразком та з коментарем.
III. Формулювання мети і завдань уроку
Тема уроку визначає подвійну мету уроку:
1) закріплення знань означень тригонометричних функцій гострого кута, їх властивостей, а також тотожностей для тригонометричних функцій певного гострого кута;
2) продовження роботи із формування вмінь практичного застосування цих відомостей.
IV. Відтворення, корекція та систематизація опорних знань
Повторення знань учнів, набутих ними під час вивчення нового матеріалу, частково відбулося в ході перевірки домашнього завдання.
Систематизувати знання учнів можна шляхом розв'язування таких завдань, як завдання на дописування та на пошук помилок (приклади таких завдань — див. попередній урок, етапи формування знань та підбиття підсумків).
V. Формування вмінь
Застосування знань у стандартних ситуаціях
Самостійна робота
Варіант 1
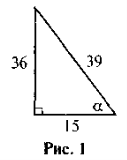
- За даними рис. 1 знайдіть cos α.
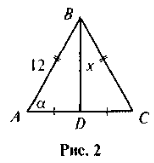
- За даними рис. 2 знайдіть х.
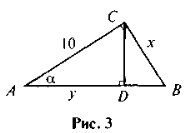
- За даними рис. З знайдіть х і у.
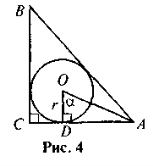
- За даними рис. 4 знайдіть АС.
Варіант 2
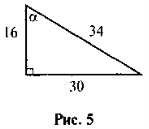
- За даними рис. 5 знайдіть sin a.
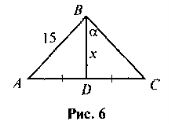
- За даними рис. 6 знайдіть х.
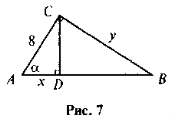
- За даними рис. 7 знайдіть х і у.
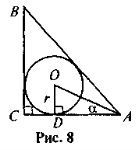
- За даними рис. 8 знайдіть АС.
Застосування знань у нестандартних ситуаціях
- Спростіть вираз:
а) 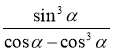 ; б) tg2 α (1 – sin α)(1 + sin α); в)
; б) tg2 α (1 – sin α)(1 + sin α); в) 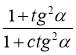 .
.
- Спростіть вираз:
а) (sin α + cos α)2 + (sin α – cos α)2; б) 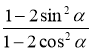 ; в)
; в) 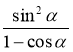 ;
;
г) 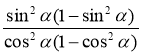 ; д)
; д) 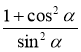 ;
;
e) (1 – sin α)2 + (1 – cos α)2 + (1 + sin α)2 + (1 + cos α)2.
- Обчисліть sin α + cos α, якщо sin α cos α = 0,48.
- Спростіть вираз:
1) 1 + cos2 α – sin2 α; 2) (1 – cos α)(1 + cos α); 3) ![]() ;
;
4) ![]() ; 5) 2 – cos2 α – sin2 α; 6)
; 5) 2 – cos2 α – sin2 α; 6) 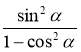 ;
;
7) 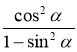 ; 8) (sin α – cos α) + 2 sin α cos α; 9)
; 8) (sin α – cos α) + 2 sin α cos α; 9) 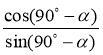 ;
;
10) 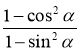 ; 11) sin2 α + sin2(90° – α); 12) 1 – cos2(90° – α);
; 11) sin2 α + sin2(90° – α); 12) 1 – cos2(90° – α);
13) sin2 α + tg2 α + cos2 α.
Підсумком цього етапу уроку є виділення основних типів задач із теми та узагальнення способів їх розв'язання (незалежно від рівня складності).
VII. Підсумки уроку
Діагностика засвоєння учнями знань та вмінь може бути проведена у формі тестової роботи.
Тестова робота
- Яка з тотожностей неправильна?
1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ; 4) sin α + cos α = 1.
; 4) sin α + cos α = 1.
- Спростіть вираз 1 – cos2 α.
1) (1 – cos α)(1 + cos α); 2) - sin2 α; 3) sin α; 4) sin2 α.
-
Знайдіть cos α, якщо sin α =
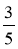 .
.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
-
Знайдіть tg α, якщо sin α =
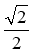 .
.
1) 4; 2) 3; 3) 2; 4) 1.
-
Обчисліть значення sin α, якщо tg α =
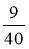 .
.
1)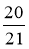 ; 2)
; 2) 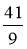 ; 3)
; 3) 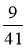 ; 4)
; 4) 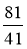 .
.
VIII. Домашнє завдання
Повторити зміст основних понять теми.
Розв'язати задачі.
- Спростіть вирази:
a) (sin α + cos α)2 + (sin α – cos α)2; б) ![]() ; в)
; в) ![]() .
.
- Обчисліть:
a) cos 45° sin 45° – sin 30°; б) sin 60o cos 30° – sin 90°;
в) tg 45° sin 45°; г) 2 ctg 30° sin 60° – cos 60°.
-
Відомо, що sin
 А + cos
А + cos А = 0,5 . Знайдіть sin
А = 0,5 . Знайдіть sin А cos
А cos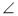 А.
А.
- Обчисліть:
1) cos α ctg α;
2) sin α · ctg α (0° < α < 90°), якщо sin α = ![]() .
.
- Спростіть вирази:
1) (sin α + cos α)2 + (sin α – cos α)2; 2) 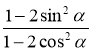 ;
;
3) (1 + sin α + cos α)(sin α + cos α – 1); 4) 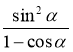 ;
;
5) 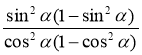 ; 6)
; 6) ![]() ;
;
7) (1 – sin α)2 + (1 – cos α)2 + (1 + sin α)2 + (1 + cos α)2.


про публікацію авторської розробки
Додати розробку
