Розв’язування задач з використанням пропорції

Розв’язування задач з використанням пропорції

­Дидактична мета: формувати уміння, навички складати пропорцію до задач та розв’язувати їх; показати прикладне й практичне значення теми; продемонструвати різноманітність застосування математики в реальному житті в різних сферах;

Розвиваюча мета: розвивати бажання пізнавати нове; розвивати пам’ять, увагу;

Виховна мета: виховувати інтерес до предмета, культуру математичного мовлення, працелюбність, позитивне ставлення до навчання;

Обладнання: мультимедійне обладнання, роздаткові картки, презентація.

Хід уроку

І. Перевірка домашнього завдання.

Перевіряють до уроку сильні учні по рядах. Якщо виникають питання, дати відповідь на уроці.

1) Розв’язати пропорцію

= ;

х-2 = = 25;

х=27;

2) №612

24 зош. – 60 грн;

20 зош. – х грн;

= х=;

х=50 (грн) коштують 20 зош.;

20 зош. – 50 грн;

у зош. – 45 грн;

= у=

у=18 (зош.) можна купити за 45 грн;

Відповідь: 50 грн, 18 зошитів.

ІІ. Оголошення теми й мети.

Вчитель. Тема нашого уроку «Розв’язування задач з використанням пропорції». Чому ми навчимося на уроці? Що необхідно повторити? А навіщо нам потрібно вчитися розв’язувати такі задачі? Відповіді учнів.

Дійсно, «Розум полягає не тільки в знаннях, але й в умінні застосовувати набуті знання на практиці» (Аристотель).

ІІІ. Актуалізація опорних знань.

Проводить учень.

У пропорції 3:4=6:8 назвати крайні; середні члени.

Чи істинна дана пропорція?

Як знайти невідомий член пропорції?

Якщо залежність між величинами прямо пропорційна, то 1:2=… (продовжити).

Якщо залежність між величинами прямо пропорційна і одну з них збільшили в 3 рази, то інша…

зменшили в 7 разів, то інша …

Тестові завдання (робота в парах).

Виберіть правильну відповідь на кожне з 5 тестових завдань, потім розташуйте одержані літери по порядку, і дізнаєтеся синонім до слова пропорція.

Складіть пропорцію з чисел  12; 2;   8;    3

1.      У пропорції 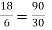 середніми членами є числа…

2.      У пропорції 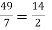крайніми членами є числа…

3.      Яка рівність випливає з пропорції 16:12=32:24 відповідно до основної властивості пропорції

4.      Знайдіть невідомий член пропорції 36:6=х:5

Вчитель. Пропорція і краса – синоніми, недарма говорять «Пропорція – це формула краси і гармонії». Середньовічний вчений Августин назвав красу «числовою рівністю». Філософ Бонавентура писав «Краси та насолоди немає без пропорційності».

Відео «Золотое сечение. Число Фибоначчи». https://www.youtube.com/watch?v=G8yLBaYQG8E

Так от, піфагорійці шукали математичне обгрунтування краси. Вони дослідили тіло людини та утвердили канон краси, за яким скульптор Поліклет створив статую «Канон».

Найкращою фігурою вважається така, в якої відношення меншої частини до більшої дорівнює відношенню більшої до всього.

Підопригора Анна провела практичне дослідження і перевірила, чи виконуються пропорції золотого перерізу в будові тіла учнів нашого класу.

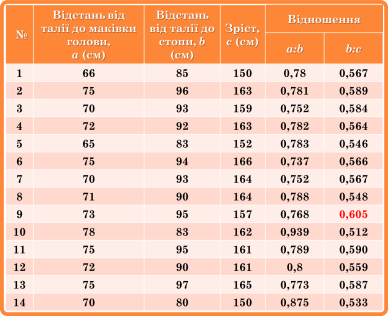
Учениця. Провівши відповідні виміри та обчислення я встановила, що відношення довжини а верхньої частини тіла до нижньої частини b в наших піддослідних значно перевищує показник 0,618, а нижньої частини до цілої трішки менший за це число. Найближчим він є у №9. Поцікавившись у вчителя біології, я можу заспокоїти вас всіх. Для нашого віку це нормально. Але нам всім обов’язково треба займатися фізичними вправами і в майбутньому наші фігури будуть ідеальними.

ІV. Формування умінь і навичок

А тепер послухайте ваших старшокласників. (Демонструється відео, записане заздалегідь з зупинками для розв’язування задач).

Учень. До вас, шестикласники, звертаємося ми, учні 10 класу, що вже дуже обре зрозуміли, що таке пропорція, та як вона допомагає нам вчитися.

Учень. Пропорція «призначить вам побачення» на уроках алгебри, геометрії, фізики, хімії, географії, біології, креслення, образотворчого мистецтва, музики.

Учень. З її допомогою можна розв’язувати задачі з цих предметів, знаходити відстані на карті і на місцевості, робити досліди і просто малювати.

Учень. Архітектор, скульптор, художник, музикант, лікар і фармацевт, інженер – всі вони знають пропорцію та її властивості.

Учень. Вивчаючи біологію, я чітко усвідомив, що вміти розв’язувати пропорції дуже важливо.

Чи знаєте ви, що деякі хвороби розвиваються через нестачу вітамінів? Вітаміни мають значний вплив на ріст, розвиток, обмін речовин.

Виключно важливим є вітамін С. У великій кількості він міститься в плодах шипшини, чорної смородини, капусті, петрушці. В хвої сосни вітаміну С в 7 разів більше, ніж в лимонах.

Склянка соку з квашеної капусти, випитої натщесерце підвищує працездатність, покращує апетит і травлення, допомагає протистояти застудним захворюванням.

Я пропоную розв’язати за допомогою пропорції наступну задачу:

У 100 г чорної смородини міститься приблизно 0,25 г вітаміну С. Визначити вміст вітаміну С в 1 кг чорної смородини. Скільки грамів чорної смородини потрібно з’їсти людині за день, якщо 1 добова доза вітаміну С складає 0,05 грама?

Розв’язання

Смородина

100 г

1 кг = 1000 г

Вітамін С

0,25 г

х г

= ; х=2,5 (г) вітаміну С в 1 кг смородини;

Смородина

100 г

у г

Вітамін С

0,25 г

0,05 г

= ; х=20 (г) смородини потрібно з’їсти за день.

Відповідь: 2,5 г; 20 г.

Учень. Я агітую вас вчитися розв’язувати задачі на пропорції. Ось послухайте, чому.

У Стародавній Греції музика – єдина з семи видів мистецтва входила до великої четвірки наук разом з арифметикою, геометрією та астрономією.

Піфагор та його учні помітили, що в основі музики лежать математичні пропорції. Це і відношення довжини струни до висоти тону і відношення між музичними проміжками і співвідношення звуків у аккордах, які дають гармонічне звучання.

Вивчення того, які відношення чисел дають красиві музичні сполучення, а які – різкі і неприємні, є цілою наукою.

Альберт Ейнштейн стверджував, що справжня математика і справжня музика потребують однакового розумового процесу.

Майбутнім музикознавцям пропоную включитися в процес розв’язування слідуючої задачі.

Музичний етюд, утворений з 3 однакових за довжиною частин триває 1 хв 15 сек. Скільки часу буде тривати етюд, складений з 5 таких самих частин?

Розв’язання

Етюд

3 ч.

5 ч.

Час

1 хв 15 с = 75 с

х с

= ; х= ;

х=125 (с) триває етюд з 5 частин;

125 с=2 хв 5 с;

Відповідь: 2 хв 5 с.

Учень. В центрі нашого міста знаходиться перлина архітектури – Свято-Покровський кафедральний собор, зведений у стилі українського бароко і який є унікальним за своїм об’ємно-просторовим рішенням. Якщо дивитися на нього з висоти пташиного польоту, він схожий на корабель.

Є привід стверджувати про поєднання в будівлі храму почерків архітектурних шкіл Растреллі, Ухтомського та місцевої школи. Краса храму в пропорційності його частин.

Для створення будь-яких проектів виконуються креслення у масштабі. З використанням масштабу можна досліджувати старовинні карти, плани, обчислювати відстані для подорожей, тож вчіться розв’язувати задачі на масштаб, адже це так цікаво!

Довжина фасаду Покровського собору на плані з масштабом 1:5000 становить 0,9 см. Яка довжина фасаду насправді?

Розв’язання

На плані

1 см

0,9 см

На місцевості

5000 см = 50 м

х м

= ; х= ;

х=45 (м)довжина фасаду насправді;

Відповідь: 45 м.

Фізкультхвилинка. Для проведення використати відео «Музика математичних ритмів».

https://www.youtube.com/watch?v=dpWg9FaOCPE

Вчитель. А я пропоную розв’язати задачу від майстра порцелянової справи.

Для приготування порцеляни беруть білу глину, пісок і гіпс у відношення 25:2:1. Скільки кожного з цих матеріалів треба взяти, щоб отримати 280 кг суміші, з якої виготовляють порцеляну?

Розв’язання

Вводимо коефіцієнт пропорційності х. Тоді білої глини 25х кг, піску 2х кг, гіпсу х кг.

Маємо рівняння:

25х+2х+х=280;

28х=280;

х=10

Білої глини - 25·10=250 (кг);

Піску - 2·10=20 (кг);

Гіпсу - 10 (кг);

Відповідь: 250 кг, 20 кг, 10 кг.

V. Підведення підсумків.

Ось і підійшов час підвести підсумок уроку?

Чи зуміли уміння розв’язувати рівняння застосовувати при розв’язуванні практичних задач

Що нового дізналися?

Що цікавого?

Чи варто вчитися розв’язувати пропорції?

VІ. Домашнє завдання.

Щоб закріпити набуті знання і вдосконалити практичні навички, необхідно:

• повторити §12-15, №614;
• скласти кросворд «Пропорція»;
• переглянути відео «Пропорции «Золотого сечения» воды».

https://www.youtube.com/watch?v=RGr8OuSh0BI