Розв’язування задач. Задачі професійного змісту. (Тема.Площі поверхонь геометричних тіл)

Розв’язування задач. Задачі професійного змісту.    (Тема.Площі поверхонь геометричних тіл)

Вступ

Математична освіта є важливою складовою загальноосвітньої підготовки. Місце математики в системі освіти визначається її роллю в інтелектуальному, соціальному та моральному розвитку особистості, розумінні будови і використання сучасної науки і техніки, нових інформаційних технологій, сприйманні наукових і технічних ідей, формуванні наукової картини світу і сучасного світогляду. Математика є опорним предметом при вивченні суміжних дисциплін (фізики, хімії, інформатики, біології, географії, економіки, креслення), тому без належної математичної підготовки неможлива повноцінна освіта сучасної людини.

Вирішальне значення для системи освіти має формуючий вплив предмета математики на розвиток логічного мислення, просторових уявлень і уяви, алгоритмічної і інформаційної культури, уваги, пам’яті.

Просторове мислення, як відомо, є складовою частиною чуттєво-образного мислення і не є апріорі визначеним, запрограмованим від народження. Воно формується в процесі індивідуального розвитку людини. Просторове мислення виникає в надрах практичної потреби орієнтації на місцевості, серед об'єктів матеріального світу. Однією з основних цілей вивчення стереометрії є усвідомлення учнями структури логічної побудови цього розділу. Обов’язковим завданням є розвиток логічного мислення просторової уяви, абстрактного мислення учнів, а також ілюстрація зв’язку геометрії з реальним життям.

                            План уроку

І. Організаційний момент

ІІ. Повідомлення теми, мети і завдань уроку

IІІ. Мотивація навчальної діяльності (розповідь викладача)

ІV. Актуалізація опорних знань (Вправа «Заповни таблицю»)

V. Розв'язування задач

VІ. Домашнє завдання

ЗО отримують диференційоване домашнє завдання із збірника до ДПА з математики.

VІІ. Підсумки уроку. Рефлексія.

Мета уроку:

Тип уроку: формування практичних  вмінь та навичок.

Обладнання: мультимедійний комплекс, картки-завдання, моделі многогранників та тіл обертання.

Хід уроку

І. Організаційний момент

ІІ. Перевірка домашньої роботи

Викладач: Як ви пам'ятаєте, ми зараз вивчаємо тему «Площі поверхонь геометричних тіл». На попередньому уроці план  розв’язання домашніх задач ми з вами обговорювали, тому я сподіваюсь, що труднощів при розв’язуванні не виникло. Давайте перевіримо відповіді, які ви отримали.

ІІІ. Повідомлення теми, мети і завдань уроку

Викладач:Ви вже знайомі з усіма формулами для знаходження площ поверхонь геометричних тіл і вмієте їх застосовувати в залежності від умови задачі. А на сьогоднішньому уроці я покажу вам як можна використати ці знання в вашій професійній діяльності. (Учні записують тему уроку в зошити). Слайд №1

IV. Мотивація навчальної діяльності

Викладач:  Сподіваюся, що цей урок пройде цікаво, з великою користю для всіх. Дуже хочу, щоб ті, хто ще байдужий до цариці всіх наук, з нашого уроку пішов з глибоким переконанням: математика - цікавий і дуже потрібний предмет. Вивчаючи геометричні тіла, ми говорили про те, де можемо з ними зустрітися у побуті чи природі. 

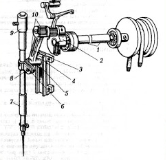Сьогодні  я хочу звернути увагу на ваше робоче місце. На малюнку зображений механізм голки швейної машинки.  Ви бачите різноманітні геометричні фігури -  циліндри, конуси, призми. Комбінації цих геометричних фігур приводять у рух механізми швейної машини.

       1. Головний вал – циліндр.

2. Кривошип – комбінація циліндра з призмою.

3. Шатун – комбінації призм циліндра.

4. Повзун – призма.

6. Поводок голковода – комбінація двох циліндрів і призми.

7. Втулка – комбінація двох циліндрів.

8. Гвинт кріплення – циліндр в комбінації з призмою.

9. Втулка – комбінація циліндрів.

      10. Палець – призма у циліндр

Сьогодні на уроці ми будемо знаходити площі поверхонь різних геометричних тіл. Для успішного розв'язання задач на уроці ви повинні вміти:

Тому перед тим як перейти до розв'язування задач я хочу, щоб ці моменти ми  з вами пригадали.

V. Актуалізація опорних знань

Викладач: Тепер перевіримо як ви знаєте формули. На кожній парті є таблиця з порожніми клітинками і конверт з варіантами відповідей. Ваше завдання кожному геометричному тілу поставити у відповідність формули для обчислення площі його поверхні.

На дошці ви  бачите  частину таблиці із зображенням  геометричних тіл. Під час того, як ви будете виконувати завдання на партах, деяких учнів я буду викликати до дошки, щоб вони по черзі  встановили відповідність між тілом і формулою для знаходження площі його поверхні.

VІ. Розв'язування задач

1.               Скільки квадратних сантиметрів шкіри потрібно , щоб зробити покришку для футбольного м'яча? (На шви і обрізки додати 5% матеріалу). Діаметр футбольного  м'яча стандартний – він дорівнює 25 см. 
2.               Скільки метрів тканини шириною 1 м потрібно для виготовлення чохла на диван (див. малюнок), якщо на шви та відходи витрачається 5% матеріалу?

 А тепер пригадаємо геометричне тіло, яке знайоме людям з древніх часів - піраміду. Піраміди служили фараонам, відповідно до їхньої релігії, східцями, по яких вони виходили на небо. Тому найстародавніші піраміди були східчастими, мали форму східців. Археологи нарахували 80 пірамід. Найбільша з них, піраміда Хеопса або велика піраміда, перше з чудес світу. Споруджена 3600 році  до нашої ери. Спочатку вона піднімалася на 147 метрів, але через підхід пісків її висота зменшилася до 137 метрів і на її вершині утворився майданчик шириною 10 метрів. Кожна сторона квадратного підніжжя піраміди складає 232 метра.

3.               3. Обчисліть площу бічної поверхні піраміди Хеопса. Відомо, що вона має форму правильної чотирикутної піраміди. Ширина грані в основі дорівнює 232 метри­­­­, а висота піраміди 147 метрів. 

VІІ. Домашнє завдання