,,Розвиток творчих здібностей учнів у процесі навчання математики.’’

Майстер-клас

 

       Доброго дня, шановні колеги!  Сучасний рух життя вимагає  швидко адаптуватися до змін, бути  здатним  застосовувати здобутті знання   у практичної діяльності. 

  Отже, темою  самоосвіти над якою я працюю є:,,Розвиток творчих здібностей учнів  у процесі навчання математики.’’ Мудрі слова: «Учень – не посудина, яку потрібно заповнити, а смолоскип, який потрібно запалити!» є провідними у моїй роботі. Намагаюсь використовувати у своїй практиці методичні прийоми,що сприяють розвитку творчого потенціалу учнів, підвищують інтерес до вивчення математики.

Хочу продемонструвати як практично застосовую різноманітні підходи у навчанні учнів математики.  Пропоную колегам бути сьогодні моїми помічниками.

Зараз ми проведемо з Вами експеримент. Перед Вами лежать чисті аркуші паперу.Ваше завдання виконувати те, що я Вам скажу, але при цьому Ви не повинні задавати жодних запитань, просто уважно виконуйте мої вказівки. Ви готові? Візьміть аркуші в руки. Зігніть їх навпіл.Так згинаємо.Відірвіть правий верхній кут. Так, ну і останній раз зігніть навпіл і останній раз відірвіть правий верхній кут. Є, зробили,  ну а тепер розгорніть будь-ласка свої аркуші і покажіть, що Ви отримали. Друг другу покажіть.А що ж таке? Покажіть. А що ж вийшло? Всі виконували мої вказівки, так? Так. А у Вас вийшли різні моделі. Покажіть ще раз,будь-ласка. Так вот ,це елементарний приклад того,що виконуючи одні й ті самі дії, ми отримуємо різний результат і це не тому, що Ви помилилися і не тому, що діти не такі розумні,а тому що, ми всі з Вами різні і по-різному сприймаємо інформацію,обробляємо,відтворюємо її. Тому навчання має бути пристосоване до індивідуальних потреб різних учнів. І це вимагає від вчителя різноманітних підходів у навчанні, де самі учні доходять висновків з допомогою вчителя, що і  намагаюсь робити і  я у своїй роботі. Отже, я роблю це так…

 Після ознайомлення учнів з темою ,,Декартові  координати на площині’’ пропоную їм пригадати всі терміни, формули, означення . Далі пропоную завдання учням і хочу запропонувати і Вам - це завдання,яке має назву Асоціативне гроно. Основне поняттям теми розміщую посередині.  А тепер навколо прямокутника напишіть терміни, які асоціюються у Вас з даним поняттям.

 Яка група готова відповідати ? Прошу 1 група,  2група.  Дякую.

Після переліку можна запропонувати учням  дати означення переліченим термінам, записати формули, використовуючи довідники.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вказаний метод застосовую під час проведення мотивації окремих питань  або під час проведення підсумкових уроків .

Намагаюсь застосовувати такі методичні прийоми, які б збуджували думку школярів, підводили їх до самостійних пошуків, висновків та узагальнень. У цьому мені допомагають Дидактичні ігри як важливий засіб успішного засвоєння учнями математичних знань, умінь і навичок Мобілізувати активність учнів і визначити ступень оволодіння теоретичним матеріалом допомагає мені ГРА ,,ХТО БІЛЬШЕ’’. Пропоную  і Вам, шановні гості виконати таке завдання: Розшифруйте анаграми (слова, отримані шляхом перестановки букв, що входять до нього).

ПЕРША ГРУПА        ДРУГА ГРУПА                ТРЕТЯ ГРУПА

 

ЧАТОК             КОДРІЗІВ         АМАЛАН

 

(ТОЧКА)         (ВІДРІЗОК)         (ЛАМАНА)      

 

Після цього пропоную учням сформулювати якомога більше суджень про свою геометричну фігуру. Виграє та група, яка запропонує більше вірних суджень. А на підсумок уроку пропоную таку гру,,ЗБЕРИ СЛОВО’’.

На дошці записані десяткові дроби:

1,52    0,235    5,5    4,05      1.42      0,1 

   Н       Ц          К      І            Е         Ь

Розмістіть  їх у порядку спадання, й  отримайте слово  (КІНЕЦЬ).

 

А зараз хочу детальніше познайомити Вас із тим, як реалізую на практиці завдання творчого характеру. На мою думку,саме завдання цього спрямування мають можливість довести, що діти реалізуються і самореалізуються через творчу діяльність і хочу запропонувати Вашій увазі деякі види творчих завдань для учнів різних вікових категорій. На уроці математики  у 5 класі під час вивчення теми: ,,Площа прямокутника і квадрата’’ ставлю перед класом таке запитання : ,,Яка площа заштрихованої фігури?’’.(мал.182). Хочу і Вам запропонувати, шановні колеги таку вправу  зробити разом.  Будь-ласка, подивіться на  свої паперові моделі  і виконав необхідні вимірювання,  знайдіть площу фігури, що заштрихована.

 Сьогодні, все більше задач, що  пропонують на ЗНО  подані у вигляді малюнків  і викликають у учнів певні труднощі. Задачи такого типу подані у великій кількості у підручниках за новою програмою, починаючи з початкової ланки до старшої, основними  функціями яких є розвиток логічного мислення учнів та ілюстрація застосування математичних знань.  Але  ці труднощі частіше стають своєрідним стимулом для вивчення. Я прошу групи презентувати результати своєї  роботи. Прошу 1 група, 2 група…

S=20*20-7*7=400-49=351(мм) до мал.182

S=(10+3+5)*10-3*3=180-9=171 cм до мал. 184

Дякую, у Вас є доповнення чи зауваження?

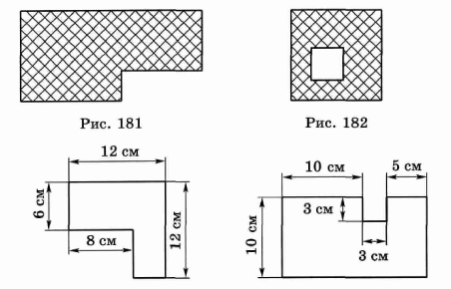
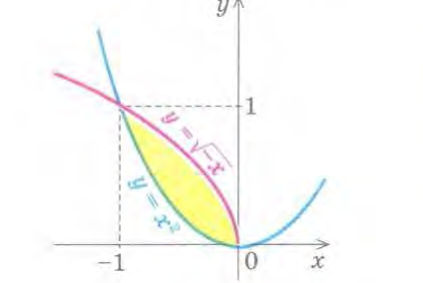
Завдання такого типу спрямовані на те, щоб опитним шляхом, самостійно прийти до висновку, що  шукана площа складається з різниці площ великого і маленького квадратів.  Одним з   таких методів, який дозволяє учням проявити творчу активність у процесі навчання математики,  самостійно ,,відкрити’’ ту чи іншу властивість є евристичний метод.

         Знайти такий кут зору, щоб навіть повсякденне стало дивовижним і таким чином відпрацювати потрібні навички допомагає один із сучасних прийомів навчання,,Здивуй”. Всі ви, мабуть, із задоволенням відвідували уроки образотворчого мистецтва. А зараз ви побуваєте у ролі художників-алгебраїстів. Кожна група одержить картку-завдання, яке  потребує вмінь та навичок побудови графіків функцій і творчих здібностей. Пропоную Вам  побудувати кожну із заданих функцій і отримати  малюнок.

Вміння побудови графіків рівнянь є одним з основних і важливих у курсі алгебри.   Лабораторно-практична робота в групах з теми:,,Красуні функції та їх графіки’’у 10 класі  дає змогу навчити учнів будувати графіки основних функцій, активізувати пізнавальну активність учнів, вміння застосовувати набуті знання в нестандартних умовах,показати красу математики в ,,красивих побудовах», перевірити навчальні досягнення  та закріпити пройдений матеріал.

Я бачу,що групи вже готові і прошу представити результати роботи. Перша група прошу…

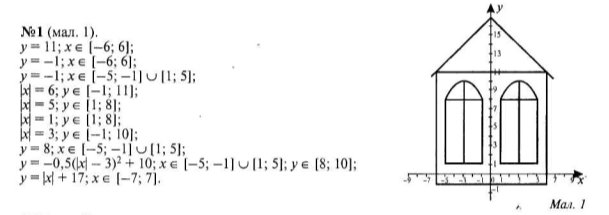
Важливу роль у навчанні математики відіграє систематичне використання історичного, прикладного, практичного матеріалу, який підвищує інтерес до вивчення предмету, розвиває пізнавальний інтерес, стимулює потяг до наукової творчості, пробуджує  критичне ставлення до фактів, дає учням уявлення про математику як невід’ємну складову  загальнолюдської  культури.

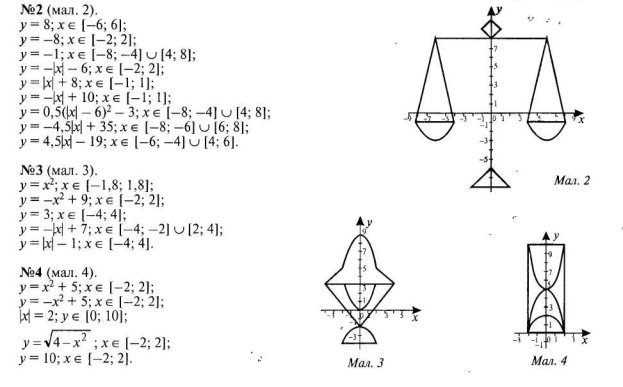
Для розвитку математичної пам’яті і творчих здібностей  школярів,підвищення емоційної насиченості уроку математики, підтримки інтересу до предмета, урахування особливостей учнів з  образним мисленням, як один із засобів, інколи у якості домашнього  завдання на вихідні, на канікули пропоную учням скласти творчі роботи у вигляді математичних казок,  віршів, ребусів, кросвордів, деяких сторінок з історії математики. Такі завдання незвичайні для уроку математики і тому –то визивають інтерес, полегшують запам’ятовування матеріалу. Казки  допомагають зрозуміти, чим живе твій учень, про що мріє, що його хвилює. Математична казка дає змогу знайти шлях до серця дитини і дозволяє увірватися на урок гумору, фантазії, винахідливості, творчості.  Персонажі казок - це числа, формули, геометричні фігури, які оживають і допомагають учню уникнути труднощів при вивчені математики. На казкових прикладах автор показує учням, як розвивалися математичні поняття та відношення, зв'язок між ними.

Залучаю учнів до виготовлення таблиць і схем,презентацій,  рефератів шаблонів  що пояснюють матеріал теми. Ця форма роботи формує в учнів уміння виокремлювати головне, встановлювати причинно-наслідкові зв’язки та сприяє активізації розумової діяльності.

Спостерігається недостатня сформованість у учнів навичок застосовувати теоретичний матеріал під час розв’язування завдань, відрив теорії від практики і формальне заучування матеріалу. Так, на уроках у 8, 9 класах проводжу роботу з конструювання означень .  Хочу і Вам запропонувати таке завдання:  Які з перелічених суттєвих властивостей однозначно визначають основні поняття теми?

 Пропоную до вашої уваги слайд :

1. Діагоналі взаємно перпендикулярні.
2. Многокутник.
3. Діагоналі перетинаються і точкою  перетину діляться пополам.
4. Протилежні сторони попарно рівні.
5. Має чотири і тільки чотири кути.
6. Має хоч один прямий кут.
7. Діагоналі рівні між собою.
8. Чотирикутник.
9. Дві сусідні сторони рівні між собою.
10.  Паралелограм.
11. Чотири сторони і чотири кути рівні між собою.
12.  Прямокутник.
13.  Ромб.

 Пропоную Вам вибрати різні сукупності суттєвих властивостей, які однозначно визначають одне і теж поняття. Робіть необхідні записи і прошу  групи представити свої результати. Називайте властивості: перша група….друга група…

Чотирикутник = 2+5

Паралелограм = 8+4

Паралелограм = 8+3

Паралелограм = 2+5+4

Ромб =10+9

Квадрат =13+6

Квадрат = 10 +11

Квадрат = 2+5+4+9+6

Квадрат = 12+9

Ромб = 8+3+1

Ромб=10+1

Прямокутник = 10+6

Прямокутник = 8+3+6

Квадрат = 10+9+7

Дякую.

Сума номерів означає таку сукупність суттєвих властивостей, яка необхідна і достатня для однозначного визначення поняття. Це завдання вимагає синтезу знань і їх узагальнення. Учням можна запропонувати  додому придумати дидактичну гру з теми:,,Чотирикутники’’; або дослідницьку роботу. Дослідити проблему:,,Що буде, якщо діагональ паралелограма є бісектрисою кута…” і підготувати письмовий звіт.

Наступний вид роботи , який я хочу Вам презентувати і пропоную учням, особливо старших класів- алгоритмічний підхід. Пропоную учням в групах  скласти алгоритм вибору  правила, яким необхідно користуватися при розв’язанні, наприклад, комбінаторних задач або відредагувати текст визначення або прочитати твердження і довести його істинність або хибність.

 

 

В процесі навчання математиці намагаюся прилучати учнів до самостійного проведення висновків за аналогією. Наведу приклад:

• Як зміниться площа прямокутника, якщо його основу звеличити у 2 рази, а бічну сторону зменшити також у 2 рази?
• Площа не зміниться.
• Так. А якщо основу прямокутника звеличити на 20 %, а бічну сторону зменшити на 20%?
• Площа не зміниться.відповідають учні

Остання відповідь не вірна. Звісно, позначимо основу прямокутника через a, а бічну сторону через b, маємо: S= a* b.

Відповідно до умови основа зміненого прямокутника a1=a+0,2a і бічна сторона b1=b-0,2b. Тоді  нова площа буде S1=a1*b1=a(1+0,2)*b(1-0,2)=ab-0,04ab.

Тому площа прямокутника зменшиться на 4%.

Ми бачимо, що висновки, отримані по аналогії, потребують обов’язкового  обгрунтування , тому що  не виключно,що вони можуть виявитися помилковими. Отже, широке застосування  аналогії у процесі навчання математиці є одним з ефективних прийомів, здатних визвати у школярів живий інтерес до предмету, прилучити їх до того виду діяльності, що має назву дослідницьким.

Досягти оптимального результату на уроці допомагають  інформаційно-комунікаційні технології . Готуючись до уроку застосовую і використовую мультимедійне забезпечення, для задач з частковими розв’язаннями, де потрібно заповнити лише пропуски або виправити помилки, а також для задач за готовим малюнком.

 

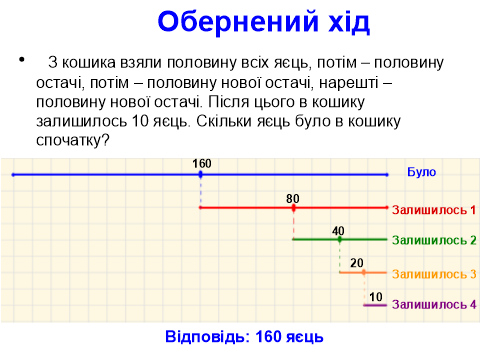
На такій діаграмі легко пояснювати умову задачі і показувати майже усне її розв’язування. Це легко здійснити за допомогою саме мультимедійної дошки, на якій поступово з’являються окремі фрагменти малюнка.

Особливо на уроках геометрії дуже зручно розв’язувати вправи та задачі за готовими малюнками. Розв’язування таких задач дає змогу економити час на уроці, не вдаючись до процесу виготовлення малюнка, привчає учнів читати рисунок, розширює математичний світогляд учнів, сприяє розвитку їхньої математичної мови.

Якщо пропонувати учням тільки завдання, що потребують автоматичного виконання дій та механічного відтворення формул, то це гальмує їх розвиток. Тому в своїй діяльності намагаюсь оновлювати методи навчання. Зокрема, використовую метод проектів, у старших класах, який сприяє організації пошукової, дослідницької діяльності, формує уміння приймати рішення щодо напрямку та способів розв’язання проблеми. Цікавою формою формування та розвитку критичного мислення є складання сенканів за певним алгоритмом індивідуально , у парах ,групах . Пропоную і Вам, шановні колеги скласти сенкани до понять: Трикутник, Вектор, Чотирикутник.

  Сенкан допомагає підсумувати інформацію , вивчати головні ідеї , ключові думки. Метод „Сенкан” використовується для розвитку в учнів здатності узагальнювати і систематизувати інформацію. Це вимагає ретельного обмірковування на основі глибокого розуміння речей. Сенкан спонукає учнів із великого обсягу інформації відібрати головне й відтворити у стислій формі.

Ось які сенкани написали учасники груп: Презентуємо, будь-ласка перша група:

1. Трикутник.

Прямокутний, тупокутний.

Накреслити, розв’язати, дослідити.

Сума всіх сутів трикутника дорівнює 180 градусів.

Геометрична фігура.

Друга група:

2. Вектор.

Одиничний, нульовий.

Знайти, накреслити, спроектувати.

Вектор – це напрямлений відрізок.

Математичний термін.

Третя група:

3. Чотирикутник.

Опуклий, неопуклий.

Накреслити, розв’язати, описати.

Паралелограм, ромб, квадрат, прямокутник, трапеція – чотирикутники.

Геометрична фігура.

ВИСНОВОК:  Дякую моїм помічникам колегам і хочу зазначити, що      виховуючи широту поглядів, різнобічність інтересів, діалектичне вміння бачити світ не односторонньо, а у всій його складності і взаємодії ми повинні вже в школі. Багато для цього різних засобів, але виховання творчістю залишається найціннішим.  Вони повинні практикуватися кожним вчителем, практикуватися оптимально, узгоджуючись із загальним планом творчих робіт в класі і можливостями учнів, щоб збуджувати творчий порив, енергію, здібності, якими щедро наділена кожна людина. Не треба боятися різноманітності. Лише практика визначить, який з підходів є найбільш продуктивним і ефективним. Я переконана, що застосовуючи сучасні підходи до проектування уроку,  маючи бажання та вміння постійно вчитися й самовдосконалюватися, учень засвоїть навчальний матеріал та отримає можливість самореалізації через творчу діяльність.

Дякую за увагу!