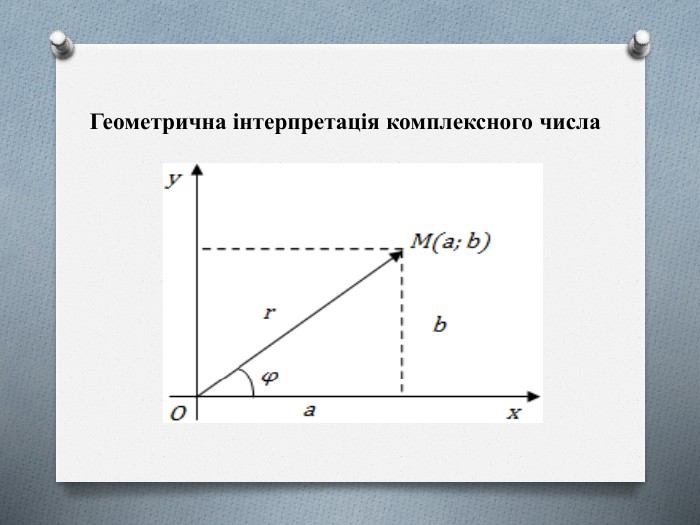
Презентація "Геометрична інтерпретація комплексних чисел. Тригонометрична форма запису комплексного числа. Дії над комплексними числами в тригонометричній формі "
Про матеріал
В презентації розглянуто теоретичні питання про перехід від алгебраїчної до тригонометричної форми запису комплексного числа. Наведено приклад виконання практичного завдання. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку