Самостійна робота "Квадратна нерівність"

Самостійна робота з алгебри 9 клас

Квадратна нерівність

4 варіанта

І варіант

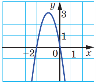1. На малюнку схематично зображено графік функції  . Знайдіть множину розв'язків нерівності

А) [-2;0]     Б)(-2;0)    В)(-∞;-2)∪(0;+∞)    Г)(-∞;-2]∪[0;+∞)

2. Розв'яжіть нерівність:

а)– х² – 2х + 3 > 0; 

3.Знайдіть область визначення функції

4. При яких значеннях a рівняння має два дійсні різні корені?

5. Земельна ділянка має форму прямокутника, одна зі сторін якого на 7 м більша за іншу. Якою має бути менша сторона ділянки, щоб її площа не перевищувала 60 м²?

IІ варіант

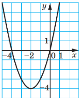1. На малюнку схематично зображено графік функції  . Знайдіть множину розв'язків нерівності

А) [-4;0]     Б)(-4;0)    В)(-∞;-4)∪(0;+∞)    Г)(-∞;-4]∪[0;+∞)

2. Розв'яжіть нерівність:

а)– х² + 4х + 5 > 0 ; 

3.Знайдіть область визначення функції

4. При яких значеннях a рівняння має два дійсні різні корені?

5. Земельна ділянка має форму прямокутника, довжина якого на 5 м більша ніж ширина. Якою має бути ширина ділянки, щоб її площа була не меншою за 36 м²?

IIІ варіант

1. На малюнку схематично зображено графік функції  . Знайдіть множину розв'язків нерівності

А) [-2;0]     Б)(-2;0)    В)(-∞;-2)∪(0;+∞)    Г)(-∞;-2]∪[0;+∞)

2. Розв'яжіть нерівність:

а) х² – 5х + 6  0;

3.Знайдіть область визначення функції

4. При яких значеннях a рівняння не має коренів?

5. Земельна ділянка має форму прямокутника, одна зі сторін якого на 7 м більша за іншу. Якою має бути менша сторона ділянки, щоб її площа  перевищувала 60 м²?

IV варіант

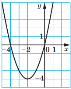1. На малюнку схематично зображено графік функції  . Знайдіть множину розв'язків нерівності

А) [-4;0]     Б)(-4;0)    В)(-∞;-4)∪(0;+∞)    Г)(-∞;-4]∪[0;+∞)

2. Розв'яжіть нерівність:

а) –х² – 4х –  3 < 0; 

3.Знайдіть область визначення функції

4. При яких значеннях a рівняння   не має коренів?

5. Земельна ділянка має форму прямокутника, довжина якого на 5 м більша ніж ширина. Якою має бути ширина ділянки, щоб її площа була не більше за 36 м²?

Відповіді:

Варіант1 

1.Б;   2. А) (-3;1); б) (-∞;-6][6;+∞)  3.[0;1)(1;3]  4. (-∞;-10)(10;+∞)

Варіант2 

1.А;  2. А) (-1;5); б) (0;4)  3. (-∞;-2][2;5) (5;+∞)  4. (-∞;-12)(12;+∞)

Варіант3 

1. Г;  2. А) [2;3];  б)  (-∞;-7)(7;+∞)  3. [0;3)(3;4]  4. (-10;10)

Варіант4 

1.В;  2.  А)  (-∞;-3)(-1;+∞);  б)  (-∞;-6][0; +∞) 3. (-∞;-5)(-5;-3] (3;+∞)  4. (-12;12)