Самостійна робота з геометрії для учнів 10 класу на тему "Вступ до стереометрії"

Варіант  1

1.            Скільки площин можна провести через пряму
   і точку, що не лежить на ній:

    А) 1;      Б) безліч;          В) жодної;       Г)  Інша відповідь.

2.   Скільки площин можна провести через дві  точки ?

     А) 1;      Б) безліч;          В) жодної;       Г) Інша відповідь.

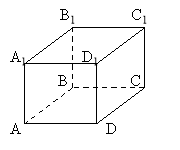
3.   На рисунку зображено куб ABCDA₁B₁C₁D₁. Прямі AA₁ і CC₁:

     А) перетинаються;       Б) паралельні;            В) Інша відповідь.

4. Яка з наведених фігур не є основною фігурою стереометрії?

      А) площина     Б) куб       В) пряма     Г) точка

5. Вказати вершину прямокутного паралелепіпеда АВСDA₁B₁C₁D₁, яка не лежить в площині (АВС).                           А) D.          Б) D₁.      В) В.      Г) С.

6. Встановіть відповідність між многогранниками  та їхніми властивостями.

       1. Прямокутний паралелепіпед.

       2. Трикутна призма.

       3. Чотирикутна піраміда.

А) Має 6 вершин.

Б) Має 6 граней.

В) Має 6 ребер.

Г) Має 8 ребер.

7. Побудуйте переріз куба ABCDA₁B₁C₁D₁  площиною, яка проходить через середини ребер АВ, AD і AA_1.

8.  Побудуйте переріз тетраедра ABCD площиною, яка проходить через ребро DС і точку перетину медіан грані АСВ.

Варіант  2

1. Скільки площин можна провести через три точки, що не лежать

на одній прямій:

    А) жодної;      Б) 1;          В) безліч;       Г)  Інша відповідь.

2.   Скільки площин можна провести через пряму і точку, що

лежить на цій прямій ?

     А) 1;      Б) безліч;          В) жодної;       Г) Інша відповідь.

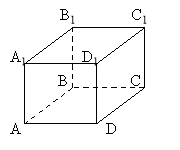
3.   На рисунку зображено куб ABCDA₁B₁C₁D₁. Прямі AA₁ і ВC:

     А) перетинаються;       Б) паралельні;            В) Інша відповідь.

4.  Яка з наведених фігур не є основною фігурою стереометрії?

      А) пряма     Б) куля       В) точка     Г) площина

5. Вказати вершину прямокутного паралелепіпеда АВСDA₁B₁C₁D₁, яка не лежить в площині (C₁ СD).                           А) D.          Б) D₁.      В) В.      Г) С.

6. Встановіть відповідність між многогранниками  та їхніми властивостями.

       1. Прямокутний паралелепіпед.

       2. Трикутна піраміда.

       3. П’ятикутна призма.

А) Має 10 вершин.

Б) Має 4 грані.

В) Має 12 ребер.

Г) Має 8 ребер.

7. Побудуйте переріз куба ABCDA₁B₁C₁D₁  площиною, що проходить через кінці трьох  ребер, що виходять з однієї вершини.  

8.  Побудуйте переріз тетраедра ABCD площиною, яка проходить через ребро ВА і точку М, що належить ребру СD.