Самостійні і контрольні роботи за курс алгебри 10 - 11 клас
Навчально-методичний посібник призначений для поточного тематичного контролю знань : проведення самостійних і контрольних робіт 10 -11 класів з алгебри.. З кожної підтеми він містить чотири варіанти самостійних робіт з системами задач середнього, достатнього і високого рівнів. Завдання кожного рівня диференційовані за трьома ступенями складності. Для тематичного оцінювання контрольні роботи дані у чотирьох варіантах.
ТЕМАТИЧНЕ ОЦІНЮВАННЯ
Самостійні і контрольні роботи
за курс алгебри
10 -11 клас
ЗМІСТ
Передмова…………………………………………………...............................4
Розділ І. Тригонометричні функції
Самостійні роботи
Тема 1. Функції…………………………………………..............................5
Тема 2. Перетворення графіків функцій……………………......................9
Тема 3. Тригонометричні функції……………………………....................14
Тематичне оцінювання (теми 1 — 3). Контрольна робота № 1…............18
Самостійні роботи
Тема 4. Співвідношення між тригонометричними
функціями одного і того ж аргументу……………....................21
Тема 5. Тригонометричні функції суми і різниці
двох чисел та подвійного аргументу………………...................25
Тема 6. Формули зведення……………………………….............................28
Тема 7. Перетворення суми і різниці тригонометричних функцій у добуток ……..............................................…....................................33
Тематичне оцінювання (теми 4 — 7). Контрольна робота № 2…..............37
Розділ ІІ. Тригонометричні рівняння і нерівності
Самостійні роботи
Тема 8. Обернені тригонометричні функції……………….........................41
Тема 9. Тригонометричні рівняння….……………………..........................44
Тема 10. Тригонометричні нерівності……………………...........................46
Тематичне оцінювання (теми 8 — 10). Контрольна робота № 3…............49
Розділ ІІІ. Степенева функція
Самостійні роботи
Тема 11. Корінь п-го степеня………………………….................................51
Тема 12. Ірраціональні рівняння….……………………..............................55
Тема 13. Степінь з раціональним показником……….................................58
Тематичне оцінювання (теми 11 — 12). Контрольна робота № 4….........62
Розділ ІV. Показникова і логарифмічна функція
Самостійні роботи
Тема 14. Показникова функція…………………………...............................66
Тема 15. Показникові рівняння….……………………..................................69
Тема 16. Показникові нерівності………………………………....................71
Тематичне оцінювання (теми 14 — 16). Контрольна робота № 5…..........73
Самостійні роботи
Тема 17. Логарифм числа………………………………................................77
Тема 18. Логарифмічна функція……………………………….....................80
Тема 19. Логарифмічні рівняння………………………………....................83
Тема 20. Логарифмічні нерівності………………………………..................85
Тематичне оцінювання (теми 16 — 20). Контрольна робота № 6..............87
І. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
ТЕМА 1. ЧИСЛОВІ ФУНКЦІЇ
Самостійні роботи
Самостійна робота № 1
Варіант 1.
Середній рівень
1. 1) Функція у = f(x) — непарна. Відомо, що f(5) = ‑12. Знайти f(‑5).
2) Функція y = (x) — спадна на області визначення. Записати в порядку зростання значення функції: (0); (‑5); (12).
2. Знайти область визначення функції:
1) y = ![]() ; 2)
; 2) ![]() .
.
3. Побудувати графік функції і записати її властивості:
1) y = ‑3x; 2) ![]() ; 3) y = x2 – 4x + 3.
; 3) y = x2 – 4x + 3.
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2. Дослідити на парність функцію y = x4 + 5x2 ‑ 3.
3. Знайти координати вершини параболи y = 2x2 – 8x + 1 і, не виконуючи побудови графіка, встановити область значень функції та проміжки монотонності.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Побудувати графік функції ![]() .
.
2. Графіком квадратичної функції y = f(x) є парабола з вершиною у точці А(6; 3), яка проходить через точку С(4; 7). Знайти проміжок спадання функції і порівняти значення функції: f(7,4) і f(6,8).
3. Дослідити на парність функцію ![]() .
.
Варіант 2.
Середній рівень
1. 1) Функція у = f(x) — парна. Відомо, що f(17) = 100. Знайти f(‑17).
2) Функція y = h(x) — зростаюча на області визначення. Записати в порядку збільшення значення функції: h(0); h(20); h(‑1).
2. Знайти область визначення функції:
1) y = ![]() ; 2)
; 2) ![]() .
.
3. Побудувати графік функції і записати її властивості:
1) y = 4x; 2) ![]() ; 3) y = x2 – 4x ‑ 5.
; 3) y = x2 – 4x ‑ 5.
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2. Дослідити на парність функцію y = 4x5 ‑ 17x3 + x.
3. Знайти координати вершини параболи y = 3x2 – 12x + 3 і, не виконуючи побудови графіка, встановити область значень функції та проміжки монотонності.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Побудувати графік функції ![]() .
.
2. Графіком квадратичної функції y = f(x) є парабола з вершиною у точці А(‑1; 3), яка проходить через точку з ординатою ‑4. Знайти проміжок спадання функції і порівняти значення функції: f(1,6) і f(2,2).
3. Дослідити на парність функцію ![]() .
.
Варіант 3.
Середній рівень
1. 1) Функція у = (x) — парна. Відомо, що (0,2) = ‑12. Знайти (‑0,2).
2) Функція y = f(x) — спадна на проміжку ![]() . Записати в порядку збільшення значення функції: f(14); f(0); f(3).
. Записати в порядку збільшення значення функції: f(14); f(0); f(3).
2. Знайти область визначення функції:
1) y = ![]() ; 2)
; 2) ![]() .
.![]()
3. Побудувати графік функції і записати її властивості:
1) y = 3x + 1; 2) ![]() ; 3) y = x2 – 6x + 5.
; 3) y = x2 – 6x + 5.
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2. Дослідити на парність функцію y = x7 – x3 +5х.
3. Знайти координати вершини параболи y = ‑2x2 + 4x + 1 і, не виконуючи побудови графіка, встановити область значень функції та проміжки монотонності.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Побудувати графік функції ![]() .
.
2. Графіком квадратичної функції y = f(x) є парабола з вершиною у точці А(1; 3), яка перетинає пряму у = 4. Знайти проміжки зростання і спадання функції і порівняти значення f(‑41) і f(‑10).
3. Дослідити на парність функцію ![]() .
.
Варіант 4.
Середній рівень
1. 1) Функція у =(x) — непарна. Відомо, що (‑3) = 17. Знайти (3).
2) Функція y = f(x) — зростаюча на проміжку ![]() . Записати в порядку збільшення значення функції: f(20); f(0); f(1).
. Записати в порядку збільшення значення функції: f(20); f(0); f(1).
2. Знайти область визначення функції:
1) y = ![]() ; 2)
; 2) ![]() .
.
3. Побудувати графік функції і записати її властивості:
1) y = 4x ‑ 1; 2) ![]() ; 3) y = x2 – 6x +8 .
; 3) y = x2 – 6x +8 .
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2. Дослідити на парність функцію y = 4x6 + 2x4 + 3.
3. Знайти координати вершини параболи y = ‑3x2 + 18x + 3 і, не виконуючи побудови графіка, встановити область значень функції та проміжки монотонності.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Побудувати графік функції ![]() .
.
2. Графіком квадратичної функції y = f(x) є парабола з вершиною у точці А(1; 3), яка не перетинає пряму у = 4. Знайти проміжок спадання функції і порівняти значення функції f(17) і f(27).
3. Дослідити на парність функцію ![]() .
.
ТЕМА 2. ПЕРЕТВОРЕННЯ ГРАФІКІВ ФУНКЦІЙ
Самостійна робота № 2
Варіант 1.
Середній рівень
- 1) Задати формулою функцію, графік якої одержують з графіка функції у = x3 в результаті його:
а) симетрії відносно осі х;
б) паралельного перенесення уздовж осі у на 5 одиниць;
в) розтягу від абсцис у 4 рази;
г) стиску до абсцис удвічі;
д) паралельного перенесення уздовж осі абсцис на 6 одиниць;
е) паралельного перенесення уздовж осі абсцис на – 4 одиниці.
2) В одній і тій самій системі координат схематично побудувати графіки функцій: y = x2; y = ‑x2; y = x2 + 1; y = (x + 4)2.
- Графіком функції у = f(x) є ламана АВС, де А(‑3; 0), В(0; 2) і С(3; 0). Побудувати графік функції:
а) у = f(x); б) у = 3f(x); в) у = ![]() f(x); г) у = ‑3f(x).
f(x); г) у = ‑3f(x).
- Побудувати графік функції y = (x – 2)2+ 3.
Достатній рівень
1. 1) Задати формулою функцію, графік якої одержують у результаті послідовного виконання перетворень:
а) розтягу графіка функції ![]() від абсцис у 4 рази і симетрією одержаного графіка відносно осі абсцис;
від абсцис у 4 рази і симетрією одержаного графіка відносно осі абсцис;
б) паралельного перенесення графіка функції ![]() , при якому його вершина переходить у точку з координатами (3; 5).
, при якому його вершина переходить у точку з координатами (3; 5).
2) Схематично побудувати графік функції ![]() .
.
2. Побудувати графік функції y = ‑(x + 3)2 + 8.
3. Записати функції, графіки яких утворюються з графіка функції y = (x) в результаті його:
а) стиску осі ординат у 3 рази;
б) розтягу від осі ординат у 7 разів;
в) симетрії відносно осі y.
Високий рівень
1. 1) Побудувати схематично графік функції y = ![]()
2) Графіком функції y = (x) є ламана ABC де А(‑4; 0), В(0; 2) і С(4; 0).Побудувати графік функції:
а) y = (4x); б) ![]() .
.
2. Побудувати графік функції ![]() .
.
3. Побудувати графік функції ![]() .
.
Варіант 2.
Середній рівень
1. 1) Задати формулою функцію, графік якої одержують з графіка функції у = ![]() в результаті його:
в результаті його:
а) симетрії відносно осі х;
б) паралельного перенесення уздовж осі у на ‑3 одиниці;
в) розтягу від осі абсцис у 7 разів;
г) стиску до осі абсцис у 3 рази;
д) паралельного перенесення уздовж осі абсцис на 8 одиниць;
е) паралельного перенесення вздовж осі абсцис на – 5 одиниць.
2) В одній і тій самій системі координат схематично побудувати графіки функцій: y = x3; y = ‑x3; y = x3 ‑ 8; y = (x ‑ 4)3.
- Графіком функції у = f(x) є ламана АВС, де А(0; 0), В(2; 3) і С(4; 0). Побудувати графік функції:
а) у = f(x); б) у = 2f(x); в) у = ‑2f(x); г) у = ![]() f(x).
f(x).
- Побудувати графік функції y = (x + 2)2 ‑ 4.
Достатній рівень
1. 1) Задати формулою функцію, графік якої одержують у результаті послідовного виконання перетворень:
а) стиску графіка функції ![]() до осі абсцис у 3 рази і симетрією одержаного графіка відносно осі абсцис;
до осі абсцис у 3 рази і симетрією одержаного графіка відносно осі абсцис;
б) паралельного перенесення графіка функції ![]() , при якому його вершина переходить у точку з координатами (‑2; 7).
, при якому його вершина переходить у точку з координатами (‑2; 7).
2) Схематично побудувати графік функції ![]() .
.
2. Побудувати графік функції y = ‑(x ‑ 2)2 + 4.
3. Записати функції, які утворюються з графіка функції y = ![]() в результаті його:
в результаті його:
а) стиску до осі ординат у 5 разів;
б) розтягу від точки (0; 0) вздовж осі абсцис у 3 рази;
в) симетрії відносно осі y.
Високий рівень
1. 1) Побудувати схематично графік функції y = ![]()
2) Графіком функції y = (x) є ламана ABC, де А(‑3; 0), В(0; 4) і С(3; 0). Побудувати графік функції:
а) y = (3x); б) ![]() .
.
2. Побудувати графік функції ![]() .
.
3. Побудувати графік функції ![]() .
.
Варіант 3.
Середній рівень
1. 1) Задати формулою функцію, графік якої одержують з графіка функції у = ![]() в результаті його:
в результаті його:
а) симетрії відносно осі х;
б) паралельного перенесення вздовж осі у на ‑5 одиниці;
в) розтягу від точки (0; 0) вздовж осі ординат у 3 рази;
г) стиску до точки (0; 0) вздовж осі ординат у 4 рази;
д) паралельного перенесення вздовж осі абсцис на 7 одиниць;
е) паралельного перенесення вздовж осі абсцис на – 6 одиниць.
2) В одній і тій самій системі координат схематично побудувати графіки функцій: y = ![]() ; y = ‑
; y = ‑![]() ; y =
; y = ![]() + 2; y =
+ 2; y = ![]() .
.
- Графіком функції у = f(x) є ламана АВС, де А(‑2; 0), В(0; 4) і С(2; 0). Побудувати графік функції:
а) у = f(x); б) у = 2f(x); в) у = ![]() f(x); г) у = ‑
f(x); г) у = ‑![]() f(x).
f(x).
- Побудувати графік функції y = (x ‑ 1)2 + 3.
Достатній рівень
1. 1) Задати формулою функцію, графік якої одержують у результаті послідовного виконання перетворень:
а) розтягу графіка функції ![]() від осі абсцис у 5 разів і симетрією одержаного графіка відносно осі абсцис;
від осі абсцис у 5 разів і симетрією одержаного графіка відносно осі абсцис;
б) паралельного перенесення графіка функції ![]() , при якому його вершина переходить у точку з координатами (4; ‑5).
, при якому його вершина переходить у точку з координатами (4; ‑5).
2) Схематично побудувати графік функції ![]() .
.
2. Побудувати графік функції y = ‑(x + 2)2 + 4.
3. Записати функції, які утворюються з графіка функції y = ![]() в результаті його:
в результаті його:
а) стиску до осі ординат у 7 разів;
б) розтягу від осі ординат у 2 рази;
в) симетрії відносно осі y.
Високий рівень
1. 1) Побудувати схематично графік функції y = ‑![]()
2) Графіком функції y = (x) є ламана ABC, де А(0; 0), В(3; ‑2) і С(6; 0). Побудувати графік функції:
а) y = (3x); б) ![]() .
.
2. Побудувати графік функції ![]() , подавши її у вигляді
, подавши її у вигляді ![]() .
.
3. Побудувати графік функції ![]() .
.
Варіант 4.
Середній рівень
1. 1) Задати формулою функцію, графік якої одержують з графіка функції у = ![]() в результаті його:
в результаті його:
а) симетрії відносно осі х;
б) паралельного перенесення уздовж осі у на ‑2 одиниці;
в) розтягу від осі абсцис у 3 рази;
г) стиску до осі абсцис у 4 рази;
д) паралельного перенесення уздовж осі абсцис на 5 одиниць;
е) паралельного перенесення уздовж осі абсцис на – 6 одиниць.
2) В одній і тій самій системі координат схематично побудувати графіки функцій: y = ![]() ; y = ‑
; y = ‑![]() ; y =
; y = ![]() ‑ 2; y =
‑ 2; y = ![]() .
.
2. Графіком функції у = f(x) є ламана АВС, де А(1; 0), В(3; 4) і С(5; 0). Побудувати графік функції:
а) у = f(x); б) у = 2f(x); в) у = ![]() f(x); г) у = ‑
f(x); г) у = ‑![]() f(x).
f(x).
3. Побудувати графік функції y = (x ‑ 3)2 ‑ 8.
Достатній рівень
1. 1) Задати формулою функцію, графік якої одержують у результаті послідовного виконання перетворень:
а) розтягу графіка функції ![]() від осі абсцис у 5 разів і симетрією одержаного графіка відносно осі абсцис;
від осі абсцис у 5 разів і симетрією одержаного графіка відносно осі абсцис;
б) паралельного перенесення графіка функції ![]() , при якому його вершина переходить у точку з координатами (‑4; ‑7).
, при якому його вершина переходить у точку з координатами (‑4; ‑7).
2) Схематично побудувати графік функції ![]() .
.
2. Побудувати графік функції y = ‑(x + 2)2 ‑ 1.
3. Записати функції, які утворюються з графіка функції y = ![]() в результаті його:
в результаті його:
а) стиску до осі ординат у 10 разів;
б) розтягу від осі ординат у 5 разів;
в) симетрії відносно осі y.
Високий рівень
1. 1) Побудувати схематично графік функції y = ‑![]()
2) Графіком функції y = (x) є ламана ABC, де А(0; 0), В(2; 2) і С(4; 0). Побудувати графік функції:
а) y = (2x); б) ![]() .
.
2. Побудувати графік функції ![]() , подавши її у вигляді
, подавши її у вигляді ![]() .
.
3. Побудувати графік функції ![]() .
.
ТЕМА 3. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Самостійна робота № 3
Варіант 1.
Середній рівень
-
1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола (0; 0) на кут радіан відображається у точку P
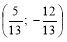 . Записати:
. Записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = cos x на проміжку ![]() .
.
- Обчислити:
1) sin 0 + cos 180 + ctg 90; 2) ![]() .
.
3. 1) Знайти область визначення функції: а) y = 2tg x; б) ![]() ;
;
2) Знайти множину значень функції: а) y = 2sin x; б) y = cos x + 3.
Достатній рівень
1. 1) Побудувати систему координат і одиничне коло із центром у початку координат, узявши за одиничний відрізок 4 клітинки. Зобразити:
а) кути (1 і 2) такі, що sin = ![]() ;
;
б) кути (1 і 2) такі, що tg = 2.
2) Побудувати графік функції y = 2sin x і записати її властивості.
3) Знайти область значень функції y = 3cos x + 5.
2. Знайти область визначення функції y = tg ![]() .
.
3. Знайти період функції:
а) y = sin 4x; б) y = cos ![]() ; в) y = tg 2x.
; в) y = tg 2x.
Високий рівень
1. 1) Побудувати графік функції y = 2sin ![]() і записати її властивості.
і записати її властивості.
2) Знайти область визначення функції ![]() .
.
2. Знайти область значень функції y = ![]()
3. Побудувати графік функції y = tg x + |tg x|.
Варіант 2.
Середній рівень
-
1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола О (0;0) на кут радіан відображається у точку P
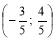 . Записати:
. Записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = sin x на проміжку ![]() .
.
- Обчислити:
1) sin 90 + cos 0 + tg 0; 2) ![]() .
.
3. 1) Знайти область визначення функції: а) y = ‑3tg x; б) ![]() ;
;
2) Знайти множину значень функції: а) y = 4sin x; б) y = cos x + 5.
Достатній рівень
1. 1) Побудувати систему координат і одиничне коло із центром у початку координат, узявши за одиничний відрізок 3 клітинки. Зобразити:
а) кути (1 і 2) такі, що cos = ![]() ;
;
б) кути (1 і 2) такі, що ctg = 2.
2) Побудувати графік функції y = 3cos x і записати її властивості.
3) Знайти область значень функції y = 4sin x + 5.
2. Знайти область визначення функції y = ctg ![]() .
.
3. Знайти період функції:
а) y = sin 2x; б) y = cos ![]() ; в) y = ctg 2x.
; в) y = ctg 2x.
Високий рівень
1. 1) Побудувати графік функції y = 4cos ![]() і записати її властивості.
і записати її властивості.
2) Знайти область визначення функції ![]() .
.
2. Знайти область значень функції y = ![]()
3. Побудувати графік функції y = ctg x + |ctg x|.
Варіант 3.
Середній рівень
1. 1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола О (0; 0) на кут радіан відображається у точку P ![]() . Записати:
. Записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = tg x на проміжку ![]() .
.
- Обчислити:
1) 2sin 30 + ![]() cos 30; 2)
cos 30; 2) ![]() .
.
3. 1) Знайти область визначення функції: а) y = ![]() tg x; б) y = 2ctg x;
tg x; б) y = 2ctg x;
2) Знайти множину значень функції: а) y = ![]() cos x; б) y = sin x + 7.
cos x; б) y = sin x + 7.
Достатній рівень
1. 1) Побудувати систему координат і одиничне коло, взявши за одиничний відрізок 4 клітинки. Зобразити:
а) кути (1 і 2) такі, що sin = ![]() ;
;
б) кути (1 і 2) такі, що ctg = ‑2.
2) Побудувати графік функції y = 3sin x і записати її властивості.
3) Знайти область значень функції y = ‑3sin x + 4.
2. Знайти область визначення функції y = tg 4x.
3. Знайти період функції:
а) y = sin ![]() ; б) y = cos 4x; в) y = tg
; б) y = cos 4x; в) y = tg ![]() .
.
Високий рівень
1. 1) Побудувати графік функції y = 3sin 4x і записати її властивості.
2) Знайти область визначення функції ![]() .
.
2. Знайти область значень функції y = ![]()
3. Побудувати графік функції y = sin x + |sin x|.
Варіант 4.
Середній рівень
-
1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола О (0; 0) на кут радіан відображається у точку P
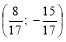 . Записати:
. Записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = ctg x на проміжку ![]() .
.
- Обчислити:
1) ![]() cos 45 +
cos 45 + ![]() sin 60; 2)
sin 60; 2) ![]() .
.
3. 1) Знайти область визначення функції: а) y = 0,1tg x; б) y = 4,3ctg x.
2) Знайти множину значень функції: а) y = 2cos x; б) y = sin x + 10.
Достатній рівень
1. 1) Побудувати систему координат і одиничне коло, взявши за одиничний відрізок 3 клітинки. Зобразити:
а) кути (1 і 2) такі, що cos = ![]() ;
;
б) кути (1 і 2) такі, що tg = ‑2.
2) Побудувати графік функції y = 2cos x і записати її властивості.
3) Знайти область значень функції y = ‑2cos x + 5.
2. Знайти область визначення функції y = ctg 4x.
3. Знайти період функції:
а) y = sin ![]() ; б) y = cos 8x; в) y = ctg
; б) y = cos 8x; в) y = ctg ![]() .
.
Високий рівень
1. 1) Побудувати графік функції y = 3cos 2x і записати її властивості.
2) Знайти область визначення функції ![]() .
.
2. Знайти область значень функції y = ![]()
3. Побудувати графік функції y = cos x + |cos x|.
Тематичне оцінювання: теми 1 — 3
Контрольна робота 1
Варіант 1.
Середній рівень
-
1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола О (0; 0) на кут відображається у точку P
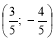 . Виконати рисунок, узявши за одиничний відрізок 5 клітинок, і записати:
. Виконати рисунок, узявши за одиничний відрізок 5 клітинок, і записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = sin x на проміжку ![]() і позначити на осі абсцис точки, в яких значення синуса дорівнює
і позначити на осі абсцис точки, в яких значення синуса дорівнює ![]() .
.
- Знайти область визначення функції:
а) ![]() ; б) y = 4cos x; г) y = 8tg x.
; б) y = 4cos x; г) y = 8tg x.
3. Знайти область значень функції: а) y = 10sin x; б) y = 12 + cos x.
Достатній рівень
- 1) Побудувати графік функції y = 4sin x і записати її властивості.
2) Знайти область значень функції y = 5cos x + 8.
- Знайти область визначення функції y = tg 2x.
3. Знайти період функції: а) y = sin ![]() ; в) y = ctg 8x.
; в) y = ctg 8x.
Високий рівень
-
1) Побудувати графік функції y = 3cos
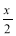 і записати її властивості.
і записати її властивості.
2) Знайти період функції ![]() .
.
-
Дослідити на парність функцію y =
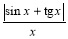 .
.
- Побудувати графік функції y = |tg x|.
Варіант 2.
Середній рівень
1. 1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола О (0; 0) на кут відображається у точку P ![]() . Виконати рисунок, взявши за одиничний відрізок 4 клітинки, і записати:
. Виконати рисунок, взявши за одиничний відрізок 4 клітинки, і записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = cos x на проміжку ![]() і позначити на осі абсцис точки, в яких значення косинуса дорівнює ‑
і позначити на осі абсцис точки, в яких значення косинуса дорівнює ‑![]() .
.
- Знайти область визначення функції:
а) ![]() ; б) y = ‑5cos x; г) y = 10tg x.
; б) y = ‑5cos x; г) y = 10tg x.
3. Знайти область значень функції: а) y = 12sin x; б) y = 14 + cos x.
Достатній рівень
1. 1) Побудувати графік функції y = 4cos x і записати її властивості.
2) Знайти область значень функції y = 12sin x + 3.
2. Знайти область визначення функції y = ctg ![]() .
.
3. Знайти період функції: а) y = cos 6x; в) y = tg ![]() .
.
Високий рівень
1. 1) Побудувати графік функції y = 3sin 2x і записати її властивості.
2) Знайти період функції ![]() .
.
2. Дослідити на парність функцію y = ![]() .
.
3. Побудувати графік функції y = |ctg x|.
Варіант 3.
Середній рівень
1. 1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола О (0; 0) на кут відображається у точку P ![]() . Виконати рисунок, взявши за одиничний відрізок 3 клітинки і записати:
. Виконати рисунок, взявши за одиничний відрізок 3 клітинки і записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = tg x на проміжку ![]() і позначити на осі абсцис точки, в яких значення тангенса дорівнює 1.
і позначити на осі абсцис точки, в яких значення тангенса дорівнює 1.
- Знайти область визначення функції:
а) ![]() ; б) y = 12sin x; г) y = 16ctg x.
; б) y = 12sin x; г) y = 16ctg x.
3. Знайти область значень функції: а) y = 14sin x; б) y = 7 + cos x.
Достатній рівень
1. 1) Побудувати графік функції y = ‑2sin x і записати її властивості.
2) Знайти область значень функції y = ‑4cos x + 3.
2. Знайти область визначення функції y = tg ![]() + 1.
+ 1.
3. Знайти період функції: а) y = cos ![]() ; в) y = tg 6x.
; в) y = tg 6x.
Високий рівень
1. 1) Побудувати графік функції y = 2cos ![]() і записати її властивості.
і записати її властивості.
2) Знайти період функції ![]() .
.
2. Дослідити на парність функцію y = ![]() .
.
3. Побудувати графік функції y = tg |x|.
Варіант 4.
Середній рівень
1. 1) Початкова точка P0 (1; 0) одиничного кола при повороті навколо центра кола О (0; 0) на кут відображається у точку P ![]() . Виконати рисунок, узявши за одиничний відрізок 4 клітинки і записати:
. Виконати рисунок, узявши за одиничний відрізок 4 клітинки і записати:
а) sin ; б) cos ; в) tg ; г) ctg .
2) Побудувати графік функції y = ctg x на проміжку ![]() і позначити на осі абсцис точки, в яких значення котангенса дорівнює ‑1.
і позначити на осі абсцис точки, в яких значення котангенса дорівнює ‑1.
2. Знайти область значень функції:
а) ![]() ; б) y =
; б) y = ![]() cos x; г) y = 7ctg x.
cos x; г) y = 7ctg x.
3. Знайти множину значень функції: а) y = 20cos x; б) y = 9 + sin x.
Достатній рівень
1. 1) Побудувати графік функції y = ‑2cos x і записати її властивості.
2) Знайти область значень функції y = ‑5sin x + 4.
2. Знайти область визначення функції y = ctg 4x + 5.
3. Знайти період функції: а) y = sin 10x; в) y = ctg ![]() .
.
Високий рівень
1. 1) Побудувати графік функції y = 2sin 4x і записати її властивості.
2) Знайти період функції ![]() .
.
2. Дослідити на парність функцію y = ![]() .
.
3. Побудувати графік функції y = ctg |x|.
ТЕМА 4.СПІВВІДНОШЕННЯ МІЖ ТРИГОНОМЕТРИЧНИМИ ФУНКЦІЯМИ ОДНОГО Й ТОГО САМОГО АРГУМЕНТУ
Самостійні роботи
Самостійна робота № 1
Варіант 1.
Середній рівень
Спростити вираз (1 — 2):
1. 1) sin2 17 + cos2 17; 2) tg![]() ctg
ctg![]() ; 3) 1 + tg2 4.
; 3) 1 + tg2 4.
2. 1) 1 ‑ sin2 29; 2) –sin2 ‑ cos2 ; 3) ![]() .
.
3. Обчислити:
1) sin , tg , ctg , якщо cos = 0,6 і ![]() .
.
2) cos2 , якщо tg = ‑3.
Спростити вираз:
3) tg ctg + ctg2 ; 4) (sin ‑ cos )2 + 2sin cos .
Достатній рівень
1. 1) Обчислити sin , cos , tg , якщо ctg = ‑![]() і
і ![]() .
.
2) Спростити вираз ![]() ctg tg .
ctg tg .
2. Спростити вираз (1 – ctg )2 + (1 + ctg )2.
3. Довести тотожність ctg2 ‑ сos2 = cos2 ctg2 .
Високий рівень
1. 1) Відомо, що ![]() , де
, де ![]() . Знайти sin , tg , ctg .
. Знайти sin , tg , ctg .
2) Довести тотожність ![]() .
.
2. Відомо, що tg = 3. Обчислити ![]() .
.
3. Обчислити sin cos , якщо sin ‑ cos = ![]()
Варіант 2.
Середній рівень
Спростити вираз (1 — 2):
1. 1) sin2 71 + cos2 71; 2) tg![]() ctg
ctg![]() ; 3) 1 + ctg2 3.
; 3) 1 + ctg2 3.
2. 1) 1 ‑ cos2 15; 2) –3sin2 ‑ 3cos2 ; 3) ![]() .
.
3. Обчислити:
1) cos , tg , ctg , якщо sin = 0,8 і ![]() .
.
2) sin2 , якщо ctg = 5.
Спростити вираз:
3) tg2 + tg ctg ; 4) (sin x + cos x)2 ‑ 2sin x cos x.
Достатній рівень
1. 1) Обчислити sin , cos , ctg , якщо tg = ‑![]() і
і ![]() .
.
2) Спростити вираз ![]() + ctg tg .
+ ctg tg .
2. Спростити вираз (1 + tg )2 + (1 – tg )2.
3. Довести тотожність tg2 ‑ sin2 = tg2 sin2 .
Високий рівень
1. 1) Відомо, що ![]() , де
, де ![]() . Знайти cos , tg і ctg .
. Знайти cos , tg і ctg .
2) Довести тотожність ![]() tg4 .
tg4 .
2. Відомо, що ctg = ‑2. Обчислити ![]() .
.
3. Обчислити sin cos , якщо sin + cos = ![]()
Варіант 3.
Середній рівень
Спростити вираз (1 — 2):
1. 1) соs2 ![]() + sin2
+ sin2 ![]() ; 2) ctg 1 tg 1; 3) ctg2 17 + 1.
; 2) ctg 1 tg 1; 3) ctg2 17 + 1.
2. 1) 1 ‑ cos2 28; 2) –cos2 ![]() ‑ sin2
‑ sin2 ![]() ; 3)
; 3) ![]() .
.
3. Обчислити:
1) sin , tg , ctg , якщо cos = ‑0,8 і ![]() .
.
2) cos2 , якщо tg = 4.
Спростити вираз:
3) 1 ‑ sin tg cos ; 4) (1 + ctg )2 ‑ 2ctg .
Достатній рівень
1. 1) Обчислити sin , cos , tg , якщо ctg = ‑![]() і
і ![]() .
.
2) Спростити вираз sin2 + cos4 (1 + tg2 ).
2. Спростити вираз (sin + cos )2 + tg2 ‑ 2sin cos .
3. Довести тотожність ![]() = cos .
= cos .
Високий рівень
1. 1) Відомо, що ![]() , де
, де ![]() . Знайти cos , tg і ctg .
. Знайти cos , tg і ctg .
2) Довести тотожність 1 – 3sin2 cos2 = sin6 + cos6 .
2. Відомо, що ctg = ‑2. Обчислити ![]() .
.
3. tg + ctg = 3. Обчислити tg2 + ctg2 .
Варіант 4.
Середній рівень
Спростити вираз (1 — 2):
1. 1) соs2 72 + sin2 72; 2) ctg ![]() tg
tg ![]() ; 3) ctg2 3 + 1.
; 3) ctg2 3 + 1.
2. 1) 1 ‑ sin2 51; 2) –2cos2 ‑ 2sin2 ; 3) ![]() .
.
3. Обчислити:
1) cos , tg , ctg , якщо sin = ‑0,6 і ![]() .
.
2) sin2 , якщо ctg = 2.
Спростити вираз:
3) 1 ‑ sin ctg cos ; 4) (1 + tg )2 ‑ 2tg .
Достатній рівень
1. 1) Обчислити sin , cos і ctg , якщо tg = ![]() і
і ![]() .
.
2) Спростити вираз cos2 + sin4 (1 + ctg2 ).
2. Спростити вираз (sin ‑ cos )2 + ctg2 + 2sin cos .
3. Довести тотожність ![]() = sin .
= sin .
Високий рівень
1. 1) Відомо, що ![]() , де
, де ![]() . Знайти cos , tg і ctg .
. Знайти cos , tg і ctg .
2) Довести тотожність ![]() = 2 cos4 .
= 2 cos4 .
2. Відомо, що tg = 2. Обчислити ![]() .
.
3. tg + ctg = 4. Обчислити ‑tg2 ‑ ctg2 .
ТЕМА 5. ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ СУМИ І РІЗНИЦІ ДВОХ ЧИСЕЛ ТА ПОДВІЙНОГО АРГУМЕНТУ
Самостійна робота № 2
Варіант 1.
Середній рівень
Спростити вираз (1 — 2):
1. 1) cos 9cos + sin 9sin; 2) sin 7cos 2 ‑ sin 2cos 7;
3) ![]() ; 4) 2sin 15cos 15; 5) cos210 – sin2 10.
; 4) 2sin 15cos 15; 5) cos210 – sin2 10.
2. 1) cos ( + ) – cos cos ; 2) 2cos2 4 ‑ 1.
3. Використавши формулу додавання, перетворити вираз sin(60 + ).
Достатній рівень
1. Обчислити:
1) tg ![]() , якщо tg = 3;
, якщо tg = 3;
2) cos 75, подавши кут 75, як суму 30 + 45;
3) sin 2, якщо sin = 0,6 і — кут 1 чверті.
2. Знайти значення виразу ![]() .
.
3. Довести тотожність ![]() .
.
Високий рівень
1. 1) Обчислити sin ( + ), якщо ![]() ,
, ![]() , і — кути І чверті.
, і — кути І чверті.
2) Знайти tg![]() , якщо
, якщо ![]() і — кут ІІІ чверті.
і — кут ІІІ чверті.
3) Обчислити tg 2, якщо sin = ‑0,6 і ![]() .
.
2. Довести тотожність ![]() .
.
3. Довести тотожність sin 3 = 3sin ‑ 4sin3 .
Варіант 2.
Середній рівень
Спростити вираз (1 — 2):
1. 1) cos 11cos ‑ sin 11sin; 2) sin 4cos 1 + sin 1cos 4;
3) ![]() ; 4) 2sin 10cos 10; 5) cos215 – sin2 15.
; 4) 2sin 10cos 10; 5) cos215 – sin2 15.
2. 1) cos ( ‑ ) – sin sin ; 2) 1 ‑ 2sin2 4.
3. Використавши формулу додавання, перетворити вираз sin(30 ‑ ).
Достатній рівень
1. Обчислити:
1) tg ![]() , якщо tg = 4;
, якщо tg = 4;
2) cos 15, подавши кут 15, як різницю 45 ‑ 30;
3) sin 2, якщо cos = ‑0,6 і — кут ІІ чверті.
2. Знайти значення виразу 2cos(60 ‑ ) ‑ ![]() .
.
3. Довести тотожність ![]() .
.
Високий рівень
1. 1) Обчислити sin ( + ), якщо ![]() ,
, ![]() , — кут ІІ чверті, — кут ІV чверті.
, — кут ІІ чверті, — кут ІV чверті.
2) Знайти tg![]() , якщо
, якщо ![]() ,
, ![]() .
.
3) Обчислити tg 2, якщо cos = 0,8 і ![]() .
.
2. Довести тотожність ![]() .
.
3. Довести тотожність cos 3 = 4cos3 ‑ 3cos .
Варіант 3.
Середній рівень
Спростити вираз (1 — 2):
1. 1) cos 13 cos 17 ‑ sin 13 sin17; 2) sin 6 cos 2 + sin 2 cos 6;
3) ![]() ; 4) 2sin 4cos 4; 5) cos242 – sin2 42.
; 4) 2sin 4cos 4; 5) cos242 – sin2 42.
2. 1) sin cos – sin ( ‑ ); 2) 2cos2 10 ‑ 1.
3. Використавши формулу додавання, перетворити вираз cos(60 ‑ ).
Достатній рівень
1. Обчислити:
1) tg ![]() , якщо tg =
, якщо tg = ![]() ;
;
2) sin 15, подавши кут 15, як різницю 45 ‑ 30;
3) cos 2, якщо cos = ‑![]() ,
, ![]() .
.
2. Знайти значення виразу ![]() cos ‑ 2cos ( ‑ 30) + sin .
cos ‑ 2cos ( ‑ 30) + sin .
3. Довести тотожність ![]() .
.
Високий рівень
1. 1) Обчислити cos ( + ), якщо cos = 0,5, sin = ‑0,4, ![]() ,
, ![]() .
.
2) tg ( ‑ 45) = 3. Знайти tg .
3) cos = ‑![]() ,
, ![]() . Знайти tg 2.
. Знайти tg 2.
2. Довести тотожність ![]() .
.
3. Довести тотожність
sin ( + ) – sin cos3 ‑ cos sin3 = sin cos cos ( ‑ ).
Варіант 4.
Середній рівень
Спростити вираз (1 — 2):
1. 1) cos 47 cos 2 + sin 47 sin 2; 2) sin 10 cos 4 ‑ sin 4 cos 10;
3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() .
.
2. 1) sin ( + ) – sin cos ; 2) 1 – 2cos2 8.
3. Використавши формулу додавання, перетворити вираз cos(45 ‑ ).
Достатній рівень
1. Обчислити:
1) tg ![]() , якщо tg =
, якщо tg = ![]() ;
;
2) sin 75, подавши кут 75, як суму 30 + 45;
3) cos 2, якщо sin = ![]() ,
, ![]() .
.
2. Знайти значення виразу ![]() sin ( ‑ 45) ‑ sin + cos .
sin ( ‑ 45) ‑ sin + cos .
3. Довести тотожність ![]() .
.
Високий рівень
1. 1) Обчислити cos ( ‑ ), якщо sin = ![]() , cos = ‑
, cos = ‑![]() ,
, ![]() ,
, ![]() .
.
2) tg ( + 45) = 4. Знайти tg .
3) sin = 0,96, ![]() . Обчислити tg 2.
. Обчислити tg 2.
2. Довести тотожність ![]() .
.
3. Довести тотожність
cos ( ‑ ) – sin sin3 ‑ cos cos3 = sin cos sin ( + ).
ТЕМА 6. ФОРМУЛИ ЗВЕДЕННЯ
Самостійна робота № 3
Варіант 1.
Середній рівень
1. 1) Звести до тригонометричної функції кута 20:
а) sin (90 + 20); б) tg (180 ‑ 20);
2) Звести до тригонометричної функції кута ![]() :
:
а) cos![]() ; б) ctg
; б) ctg ![]() .
.
2. 1) Обчислити:
а) sin (180 ‑ 30); б) ctg (270 ‑ 60).
2) Cпростити вираз sin![]() .
.
3. 1) Обчислити: а) cos 135; б) sin 300.
2) Звести до тригонометричної функції гострого кута:
а) ctg 0,6; б) tg ![]() .
.
Достатній рівень
1. 1) За допомогою формули додавання, довести рівність sin ( + ) = ‑sin .
2) Спростити вираз sin (90 ‑ ) ‑ cos (180 ‑ ) ‑ ctg (270 + ).
3) Обчислити: а) sin ![]() ; б) tg
; б) tg![]() .
.
2. Звести до тригонометричної функції гострого кута :
а) sin ![]() ; б) cos ( ‑ ).
; б) cos ( ‑ ).
3. Обчислити: а) tg (‑330); б) cos 510.
Високий рівень
1. 1) Використавши формулу зведення, довести тотожність sin (45 + ) = cos (45 ‑ ).
2) Звести до тригонометричної функції гострого кута:
а) sin 1914; б) tg (‑1560).
3) Довести тотожність
tg ( ‑ ) – ctg ![]() ‑ cos ( ‑ ) = 2cos .
‑ cos ( ‑ ) = 2cos .
2. Довести, що коли , і — кути трикутника, то cos ( + ) = ‑cos .
3. Довести, що рівність tg 1 tg 2 tg 3… tg 87 tg 88 tg 89 = 1 правильна.
Варіант 2.
Середній рівень
1. 1) Звести до тригонометричної функції кута 35:
а) tg (180 + 35); б) cos (270 ‑ 35);
2) Звести до тригонометричної функції кута ![]() :
:
а) cos ![]() ; б) ctg
; б) ctg ![]() .
.
2. 1) Обчислити:
а) sin (180 + 60); б) tg (270 ‑ 30).
2) Cпростити вираз cos![]() .
.
3. 1) Обчислити: а) sin 135; б) cos 210.
2) Звести до тригонометричної функції гострого кута:
а) tg ![]() ; б) ctg 0,7; б) tg 1,6.
; б) ctg 0,7; б) tg 1,6.
Достатній рівень
1. 1) За допомогою формули додавання довести рівність cos ![]() = ‑sin .
= ‑sin .
2) Спростити вираз sin (180 ‑ ) + cos (90 ‑ ) + ctg (270 ‑ ).
3) Обчислити: а) cos ![]() ; б) tg
; б) tg![]() .
.
2. Звести до тригонометричної функції гострого кута :
а) cos ![]() ; б) sin ( ‑ ).
; б) sin ( ‑ ).
3. Обчислити: а) sin (‑300); б) tg 480.
Високий рівень
1. 1) Використавши формулу зведення, довести тотожність cos (45 + ) = sin (45 ‑ ).
2) Звести до тригонометричної функції гострого кута:
а) cos 2024; б) tg (‑1560).
3) Спростити вираз:
tg ( ‑ 360) – ctg ( ‑ 270) ‑ sin ( ‑ 180) ‑ cos ( + 90).
2. Довести, що коли , і — кути трикутника, то sin ( + ) = sin .
3. Обчислити суму sin 0 + sin 1 + sin 2+ sin 3… sin 357 + sin 358 + sin 359 + sin 360.
Варіант 3.
Середній рівень
1. 1) Звести до тригонометричної функції кута 15:
а) sin (180 ‑ 15); б) tg (270 + 15);
2) Звести до тригонометричної функції кута ![]() :
:
а) ctg![]() ; б) cos
; б) cos ![]() .
.
2. 1) Обчислити:
а) cos (270 ‑ 60); б) tg (180 ‑ 30).
2) Cпростити вираз sin![]() .
.
3. 1) Обчислити: а) sin 150; б) ctg 225.
2) Звести до тригонометричної функції гострого кута:
а) cos 0,9; б) tg ![]() .
.
Достатній рівень
1. 1) За допомогою формули додавання довести рівність tg ( ‑ ) = ‑tg .
2) Спростити вираз sin (90 + ) + cos (180 ‑ ) + tg (270 + ) + ctg (360 ‑ ).
3) Обчислити: а) cos ![]() ; б) tg
; б) tg![]() .
.
2. Звести до тригонометричної функції гострого кута :
а) ctg ![]() ; б) cos ( ‑ 2).
; б) cos ( ‑ 2).
3. Обчислити: а) cos 495; б) tg (‑240).
Високий рівень
1. 1) Використавши формулу зведення, довести тотожність tg (45 + ) = ctg (45 ‑ ).
2) Звести до тригонометричної функції гострого кута:
а) sin 2030; б) tg (‑865).
3) Спростити вираз:
sin ![]() + cos ( ‑ ) ‑ tg
+ cos ( ‑ ) ‑ tg ![]() + ctg (2 ‑ ).
+ ctg (2 ‑ ).
2. , і — кути трикутника. Довести, що sin ![]() = cos
= cos ![]() .
.
3. Обчислити суму tg 20 + tg 40 + tg 60+ … + tg 160 + tg 180.
Варіант 4.
Середній рівень
1. 1) Звести до тригонометричної функції кута 50:
а) sin (180 + 50); б) cos (270 ‑ 50);
2) Звести до тригонометричної функції кута ![]() :
:
а) tg![]() ; б) ctg
; б) ctg ![]() .
.
2. 1) Обчислити:
а) sin (270 + 45); б) cos (180 + 30).
2) Cпростити вираз tg![]() .
.
3. 1) Обчислити: а) sin 150; б) tg 330.
2) Звести до тригонометричної функції гострого кута:
а) cos 0,6; б) ctg ![]() .
.
Достатній рівень
1. 1) За допомогою формули додавання довести рівність tg ( + ) = tg .
2) Спростити вираз sin (270 + ) + cos (180 ‑ ) + tg (90 ‑ ) + ctg (90 + ).
3) Обчислити: а) sin ![]() ; б) ctg
; б) ctg![]() .
.
2. Звести до тригонометричної функції гострого кута :
а) tg ![]() ; б) sin ( ‑ 2).
; б) sin ( ‑ 2).
3. Обчислити: а) sin (‑315); б) cos 570.
Високий рівень
1. 1) Використавши формулу зведення, довести тотожність tg (45 ‑ ) = ctg (45 + ).
2) Звести до тригонометричної функції гострого кута:
а) cos 300; б) ctg (‑928).
3) Спростити вираз:
sin ![]() + cos ( ‑ ) ‑ tg ( ‑ ) + ctg
+ cos ( ‑ ) ‑ tg ( ‑ ) + ctg ![]() .
.
2. , і — кути трикутника. Довести, що tg ![]() = ctg
= ctg ![]() .
.
3. Обчислити суму cos 20 + cos 40 + cos 60+ … + cos 160 + cos 180.
ТЕМА 7. ПЕРЕТВОРЕННЯ СУМИ І РІЗНИЦІ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ У ДОБУТОК
Самостійна робота № 4
Варіант 1.
Середній рівень
1. Записати у вигляді добутку:
1) sin 5 + sin ; 2) sin 40 ‑ sin 10;
3) cos ![]() + cos
+ cos ![]() ; 4) cos 2 ‑ cos 7.
; 4) cos 2 ‑ cos 7.
2. Cпростити вираз:
1) sin 70 + sin 20; 2) ![]() .
.
3. Записати у вигляді добутку вираз:
1) sin 28‑ cos 66; 2) ![]() + cos .
+ cos .
Достатній рівень
1. 1) Спростити вираз![]() .
.
2) Подати у вигляді добутку вираз sin + cos .
3) Довести тотожність tg + tg = ![]() .
.
Записати у вигляді добутку (2 — 3):
2. 1 + 2cos .
3. sin + sin 3 + sin 5 + sin 7.
Високий рівень
1. Перетворити у добуток (1 — 2):
1) cos2 ‑ cos2 ; 2) sin + sin + sin ( + ).
3) Обчислити sin 5 ‑ sin 3, якщо sin = ![]() .
.
2. Використовуючи формулу різниці косинусів, довести формулу sin sin = ![]() і перетворити на суму добуток sin 10 sin 8.
і перетворити на суму добуток sin 10 sin 8.
3. , і — кути трикутника. Довести, що tg + tg + tg = tg tg tg .
Варіант 2.
Середній рівень
1. Записати у вигляді добутку (1 —4):
1) sin 7 ‑ sin ; 2) sin 2 + sin 4;
3) ![]() ; 4) cos 10 ‑ cos 20.
; 4) cos 10 ‑ cos 20.
2. Cпростити вираз:
1) sin 80 ‑ sin 10; 2) ![]() .
.
3. Записати у вигляді добутку вираз:
1) cos 25‑ sin 25; 2) ![]() + sin .
+ sin .
Достатній рівень
1. 1) Спростити вираз![]() .
.
2) Подати у вигляді добутку вираз sin ‑ cos .
3) Довести тотожність ctg + ctg = ![]() .
.
Подати у вигляді добутку (2 — 3):
2. 1 ‑ 2sin .
3. cos 2x ‑ cos 4x ‑ cos 6x + cos 8x.
Високий рівень
1. Перетворити у добуток (1 — 2):
1) sin2 ‑ sin2 ; 2) sin + sin + sin ( ‑ ).
3) Обчислити cos 2 ‑ cos 6, якщо cos = ![]() .
.
2. Використовуючи формулу різниці косинусів, довести формулу cos cos = ![]() і перетворити на суму добуток cos 55 cos 15.
і перетворити на суму добуток cos 55 cos 15.
3. , і — кути трикутника. Довести, що sin + sin + sin = 4cos ![]() cos
cos ![]() cos
cos ![]() .
.
Варіант 3.
Середній рівень
1. Записати у вигляді добутку (1 —4):
1) sin 8 + sin 2; 2) sin 50 ‑ sin 20;
3) ![]() ; 4) cos 3 ‑ cos 9.
; 4) cos 3 ‑ cos 9.
2. Cпростити вираз:
1) cos 10 + cos 50; 2) ![]() .
.
3. Записати у вигляді добутку вираз:
1) sin 2+ cos 86; 2) ![]() + sin 10.
+ sin 10.
Достатній рівень
1. 1) Спростити вираз![]() .
.
2) Подати у вигляді добутку вираз cos + sin .
3) Довести тотожність tg ‑ tg = ![]() .
.
Записати у вигляді добутку (2 — 3):
2. 1 ‑ ![]() sin .
sin .
3. cos + sin 2 + cos 3 + sin 4.
Високий рівень
1. Перетворити у добуток (1 — 2):
1) 3 – 4cos2; 2) sin ‑ sin ‑ sin ( + ).
3) Обчислити sin 3 ‑ sin 5, якщо sin = ![]() .
.
2. Довести тотожність 1 + sin + cos = ![]() cos
cos![]() cos
cos ![]() .
.
3. , і — кути трикутника. Довести, що sin 2 + sin 2 + sin 2 = 4sin sin sin .
Варіант 4.
Середній рівень
1. Записати у вигляді добутку (1 —4):
1) sin 75 + sin 5; 2) sin 12 ‑ sin 2;
3) ![]() ; 4) cos 4 ‑ cos 6.
; 4) cos 4 ‑ cos 6.
2. Cпростити вираз:
1) cos 20 ‑ cos 70; 2) ![]() .
.
3. Записати у вигляді добутку вираз:
1) cos 2+ sin 84; 2) ![]() ‑ sin 5.
‑ sin 5.
Достатній рівень
1. 1) Спростити вираз![]() .
.
2) Подати у вигляді добутку вираз sin ‑ cos .
3) Довести тотожність ctg ‑ ctg = ![]() .
.
Записати у вигляді добутку (2 — 3):
2. ![]() .
.
3. sin + cos 2 + sin 3 + cos 4.
Високий рівень
1. Перетворити у добуток (1 — 2):
1) 1 – 4sin2 ; 2) sin + sin ‑ sin ( + ).
3) Обчислити cos 3 ‑ cos 5, якщо sin = ![]() .
.
2. Довести тотожність 1 ‑ cos + sin = ![]() sin
sin![]() cos
cos ![]() .
.
3. , і — кути трикутника. Довести, що sin + sin = 2cos![]() .
.
Тематичне оцінювання: теми 4 — 7
Контрольна робота 2
Варіант 1.
Середній рівень
Спростити вираз (1 — 2):
1. 1) cos2 8 + sin2 8; 2) cos2 8 ‑ sin2 8;
3) ![]() ; 4) sin 50 + sin 40.
; 4) sin 50 + sin 40.
2. 1) cos ( + ) + sin sin ; 2) ![]() .
.
3. 1) sin = ‑0,6; < < ![]() . Обчислити: cos , tg , sin 2.
. Обчислити: cos , tg , sin 2.
2) tg = 3; 0 < < ![]() . Обчислити: cos2 , cos , tg 2.
. Обчислити: cos2 , cos , tg 2.
Достатній рівень
1. 1) ![]() ,
, ![]() . Обчислити sin , sin 2, sin 4.
. Обчислити sin , sin 2, sin 4.
2) Обчислити tg15.
3) Довести, що sin 35 + cos 65 = cos 5.
Довести тотожність (2 — 3):
2. 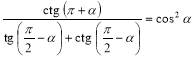 .
.
3. 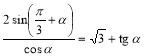 .
.
Високий рівень
1. 1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Обчислити ctg ( + ).
. Обчислити ctg ( + ).
2) Звести до тригонометричної функції гострого кута: tg 2005.
3) Довести, що ![]() .
.
2. Довести тотожність ![]() .
.
3. Довести, що ![]() .
.
Варіант 2.
Середній рівень
Спростити вираз (1 — 2):
1. 1) 1 + sin2 12 + cos2 12; 2) 2sin 12 cos 12;
3) ![]() ; 4) cos 50 + cos 40.
; 4) cos 50 + cos 40.
2. 1) sin ( ‑ ) ‑ sin cos ; 2) ![]() .
.
3. 1) cos = ‑![]() ;
; ![]() < < . Обчислити: sin , ctg , cos 2.
< < . Обчислити: sin , ctg , cos 2.
2) ctg = 3; 0 < < ![]() . Обчислити: sin , tg 2, ctg 2.
. Обчислити: sin , tg 2, ctg 2.
Достатній рівень
1. 1) ![]() ,
, ![]() . Обчислити sin , cos 2, cos 4.
. Обчислити sin , cos 2, cos 4.
2) Обчислити tg75.
3) Довести, що cos 12 ‑ sin 42 = sin 18.
Довести тотожність (2 — 3):
2. 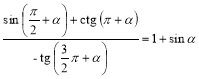 .
.
3. 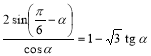 .
.
Високий рівень
1. 1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Обчислити ctg ( ‑ ).
. Обчислити ctg ( ‑ ).
2) Звести до тригонометричної функції гострого кута: sin 2005.
3) Довести, що ![]() .
.
2. Довести тотожність ![]() .
.
3. Довести, що ![]() .
.
Варіант 3.
Середній рівень
Спростити вираз (1 — 2):
1. 1) 6 + sin2 6 + cos2 6; 2) 2sin 6 cos 6;
3) ![]() ; 4) sin 50 ‑ sin 40.
; 4) sin 50 ‑ sin 40.
2. 1) sin cos ‑ sin ( + ); 2) ![]() .
.
3. 1) sin = ![]() ; 0 < <
; 0 < < ![]() . Обчислити: cos , ctg , cos 2.
. Обчислити: cos , ctg , cos 2.
2) tg = ‑2; ![]() < < 2. Обчислити: cos , tg 2, ctg 2.
< < 2. Обчислити: cos , tg 2, ctg 2.
Достатній рівень
1. 1) ![]() ,
, ![]() . Обчислити tg , tg 2, tg 4.
. Обчислити tg , tg 2, tg 4.
2) Обчислити tg105.
3) Довести, що sin 40 + cos 70 = cos 10.
Довести тотожність (2 — 3):
2. 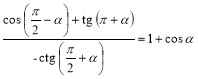 .
.
3. ![]() .
.
Високий рівень
1. 1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Обчислити ctg ( ‑ ).
. Обчислити ctg ( ‑ ).
2) Звести до тригонометричної функції гострого кут sin 594.
3) Довести, що ![]() .
.
Довести тотожність (2 — 3):
2. ![]() .
.
3. Довести, що ![]() .
.
Варіант 4.
Середній рівень
Спростити вираз (1 — 2):
1. 1) 14 + cos2 14 + sin2 14; 2) cos2 14‑ sin2 14;
3) ![]() ; 4) cos 50 ‑ cos 40.
; 4) cos 50 ‑ cos 40.
2. 1) cos ( ‑ ) ‑ cos cos ; 2) ![]() .
.
3. 1) cos = ![]() ; 0 < <
; 0 < < ![]() . Обчислити: sin , cos 2, sin 2.
. Обчислити: sin , cos 2, sin 2.
2) ctg = ‑2; ![]() < < . Обчислити: cos , tg 2, сtg 2.
< < . Обчислити: cos , tg 2, сtg 2.
Достатній рівень
1. 1) ![]() ,
, ![]() . Обчислити sin , sin 2, sin 4.
. Обчислити sin , sin 2, sin 4.
2) Обчислити sin 105.
3) Довести, що cos 20 ‑ sin 50 = sin 10.
Довести тотожність (2 — 3):
2. 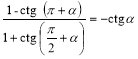 .
.
3. ![]() .
.
Високий рівень
1. 1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Обчислити ctg ( + ).
. Обчислити ctg ( + ).
2) Звести до тригонометричної функції гострого кута tg 624.
3) Довести, що ![]() .
.
Довести тотожність (2 — 3):
2. ![]() .
.
3. Довести, що ![]() .
.
ІІ. ТРИГОНОМЕТРИЧНІ РІВНЯННЯ І НЕРІВНОСТІ
ТЕМА 8. ОБЕРНЕНІ ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Самостійна робота № 1
Варіант 1.
Середній рівень
1. 1) Записати за допомогою тригонометричної функції рівність:
а) arcsin ![]() =
= ![]() ; б) arctg (‑1) = ‑
; б) arctg (‑1) = ‑![]() .
.
2) Знайти: а) arcsin ![]() ; б) arccos
; б) arccos ![]() ; в) arcctg (‑1).
; в) arcctg (‑1).
2. Побудувати графік функції y = arcsin x і записати її властивості (область визначення, область значень, монотонність, парність).
3. Накреслити систему координат і одиничне коло з центром у початку координат, взявши за одиничний відрізок 4 клітинки. Позначити точку P0 (1; 0) і побудувати дугу:
а) P0A = arcsin![]() ; б) P0B = arccos
; б) P0B = arccos![]() ; в) P0C = arctg 2.
; в) P0C = arctg 2.
Достатній рівень
1. 1) Знайти: а) ![]() ; б) tg
; б) tg![]() .
.
2) Побудувати графік функції у = 2arccos x і записати її властивості (область визначення, область значень, монотонність, парність).
2. Знайти область визначення функції у = arcsin (x – 2).
3. Розв’язати рівняння arctg (2x – 1) = ![]() .
.
Високий рівень
1. 1) Обчислити: а) sin![]() ; б) tg
; б) tg ![]() .
.
2) Побудувати графік функції y = arccos (x + 1) і записати її властивості.
3) Довести, що arcsin (‑x) = ‑arcsin x.
2. Обчислити cos ![]() .
.
3. Побудувати графік функції y = sin(arcsin x).
Варіант 2.
Середній рівень
1. 1) Записати за допомогою тригонометричної функції рівність:
а) arccos ![]() =
= ![]() ; б) arсctg
; б) arсctg ![]() = 150.
= 150.
2) Знайти:
а) arcsin ![]() ; б) arccos
; б) arccos ![]() ; в) arcctg
; в) arcctg ![]() .
.
2. Побудувати графік функції y = arccos x і записати її властивості (область визначення, область значень, монотонність, парність).
3. Накреслити систему координат і одиничне коло з центром у початку координат, взявши за одиничний відрізок 3 клітинки. Позначити точку P0 (1; 0) і побудувати дугу:
а) P0A = arcsin![]() ; б) P0B = arccos
; б) P0B = arccos![]() ; в) P0C = arctg (‑2).
; в) P0C = arctg (‑2).
Достатній рівень
1. 1) Знайти: а) ![]() ; б) tg
; б) tg![]() .
.
2) Побудувати графік функції у = 2arcsin x і записати її властивості (область визначення, область значень, монотонність, парність).
2. Знайти область визначення функції у = arccos (x + 3).
3. Розв’язати рівняння arcctg (3x – 1) = ![]() .
.
Високий рівень
1. 1) Обчислити: а) cos![]() ; б) tg
; б) tg ![]() .
.
2) Побудувати графік функції y = arcsin (x ‑ 1) і записати її властивості.
3) Довести, що arcctg (‑x) = ‑arcctg x.
2. Обчислити sin ![]() .
.
3. Побудувати графік функції y = cos(arccos x).
Варіант 3.
Середній рівень
1. 1) Записати за допомогою тригонометричної функції рівність:
а) arcsin (‑1) = ![]() ; б) arcctg
; б) arcctg ![]() =
= ![]() .
.
2) Знайти:
а) arccos ![]() ; б) arcsin
; б) arcsin ![]() ; в) arcctg
; в) arcctg ![]() .
.
2. Побудувати графік функції y = arctg x і записати її властивості (область визначення, область значень, монотонність, парність).
3. Накреслити систему координат і одиничне коло з центром у початку координат, взявши за одиничний відрізок 5 клітинок. Позначити точку P0 (1; 0) і побудувати дугу:
а) P0A = arcsin![]() ; б) P0B = arccos
; б) P0B = arccos![]() ; в) P0C = arcctg
; в) P0C = arcctg ![]() .
.
Достатній рівень
1. 1) Знайти: а) ![]() ; б) cos
; б) cos![]() .
.
2) Побудувати графік функції у = 2arcctg x і записати її властивості (область визначення, область значень, монотонність, парність).
2. Знайти область визначення функції у = arcsin (3x ‑ 1).
3. Розв’язати рівняння arccos (3x + 4) = ![]() .
.
Високий рівень
1. 1) Обчислити: а) ctg![]() ; б) cos
; б) cos ![]() .
.
2) Побудувати графік функції y = arcsin (x + 1) і записати її властивості.
3) Довести, що arcsin x = ![]() ‑arccos x.
‑arccos x.
2. Обчислити cos ![]() .
.
3. Побудувати графік функції y = ![]() .
.
Варіант 4.
Середній рівень
1. 1) Записати за допомогою тригонометричної функції рівність:
а) arccos 0 = ![]() ; б) arcsin
; б) arcsin ![]() = ‑
= ‑![]() .
.
2) Знайти:
а) arccos ![]() ; б) arctg
; б) arctg ![]() ; в) arcctg
; в) arcctg ![]() .
.
2. Побудувати графік функції y = arcctg x і записати її властивості (область визначення, область значень, монотонність, парність).
3. Накреслити систему координат і одиничне коло з центром у початку координат, взявши за одиничний відрізок 2 клітинки. Позначити точку P0 (1; 0) і побудувати дугу:
а) P0A = arcsin![]() ; б) P0B = arctg 2; в) P0C = ‑arcctg (‑3).
; б) P0B = arctg 2; в) P0C = ‑arcctg (‑3).
Достатній рівень
1. 1) Знайти: а) 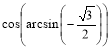 ; б) ctg
; б) ctg![]() .
.
2) Побудувати графік функції у = 2arctg x і записати її властивості (область визначення, область значень, монотонність, парність).
2. Знайти область визначення функції у = arccos ![]() .
.
3. Розв’язати рівняння arcctg (2x + 5) = ![]() .
.
Високий рівень
1. 1) Обчислити: а) sin![]() ; б) ctg
; б) ctg ![]() .
.
2) Побудувати графік функції y = arccos (x ‑ 1) і записати її властивості.
3) Довести, що arctg x = ![]() ‑arcctg x.
‑arcctg x.
2. Обчислити sin ![]() .
.
3. Побудувати графік функції y = ![]() .
.
ТЕМА 9. ТРИГОНОМЕТРИЧНІ РІВНЯННЯ
Самостійна робота № 2
Варіант 1.
Середній рівень
Розв’язати рівняння:
1. 1) sin 2x = ![]() ; 2) cos
; 2) cos ![]() = 1;
= 1;
2. tg2x + 2tg x – 3 = 0.
3. sin 3x + sin x = 0.
Достатній рівень
Розв’язати рівняння:
1. 1) 2sin2 x + 5cos x – 4 = 0; 2) cos 10x = cos2 x – sin2x.
2. sin2 x + 10cos2 x = 11sin x cos x.
3. ![]() sin x + cos x = 1.
sin x + cos x = 1.
Високий рівень
Розв’язати рівняння (1 — 2):
1. 1) 5cos x ‑ 3sin x = ![]() ; 2) tg x = tg 2x.
; 2) tg x = tg 2x.
2. sin2 x + sin2 3x = 1.
3. Розв’язати систему рівнянь 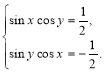
Варіант 2.
Середній рівень
Розв’язати рівняння:
1. 1) tg 2x = ![]() ; 2) sin
; 2) sin ![]() = 0;
= 0;
2. сos2x – 11cos x + 10 = 0.
3. sin 10x ‑ sin 4x = 0.
Достатній рівень
Розв’язати рівняння:
1. 1) cos 2x + 8sin x – 7 = 0; 2) sin 4x = cos2 x – sin2x.
2. 6sin2 x ‑ 7sin x cos x + cos2 x = 0.
3. sin x ‑ cos x = 1.
Високий рівень
Розв’язати рівняння (1 — 2):
1. 1) 9cos x ‑ 13sin x = ![]() ; 2) tg 4x = tg x.
; 2) tg 4x = tg x.
2. cos2 x + cos2 2x = 1.
3. Розв’язати систему рівнянь 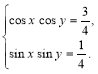
Варіант 3.
Середній рівень
Розв’язати рівняння:
1. 1) cos 4x = ![]() ; 2) tg
; 2) tg ![]() = 0;
= 0;
2. sin2x + 3sin x ‑ 4 = 0.
3. cos 3x + cos x = 0.
Достатній рівень
Розв’язати рівняння:
1. 1) cos 2x + 8sin x – 7 = 0.
2) cos x + cos 3x – cos 2x = 0.
2. 3sin2 x ‑ 8sin x cos x + 7 cos2 x = 1.
3. sin x ‑ ![]() cos x = 1.
cos x = 1.
Високий рівень
Розв’язати рівняння (1 — 2):
1. 1) 2(cos4 x – sin4 x) = 1; 2) cos x + cos 2x + cos 3x + cos 4x = 0.
2. cos 7x cos 10x = cos 2x cos 15x.
3. Розв’язати систему рівнянь ![]()
Варіант 4.
Середній рівень
Розв’язати рівняння:
1. 1) sin 4x = ![]() ; 2) tg
; 2) tg ![]() = 0;
= 0;
2. ctg2x – 8ctg x + 7 = 0.
3. cos 9x ‑ cos x = 0.
Достатній рівень
Розв’язати рівняння:
1. 1) cos 2x ‑ 10cos x – 11 = 0.
2) cos 6x = cos2 2x – sin2 2x.
2. 2sin2 x ‑ 8sin x cos x + 8 cos2 x = 1.
3. cos x + ![]() sin x = 2.
sin x = 2.
Високий рівень
Розв’язати рівняння (1 — 2):
1. 1) cos4 1,5x – sin4 1,5x = ![]() ; 2) cos 3x + sin 3x = cos x + sin x.
; 2) cos 3x + sin 3x = cos x + sin x.
2. sin 5x sin 3x + cos 7x cos x = 0.
3. Розв’язати систему рівнянь 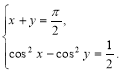
ТЕМА 10. ТРИГОНОМЕТРИЧНІ НЕРІВНОСТІ
Самостійні роботи
№ 45. Варіант 1.
Середній рівень
Розв’язати нерівність:
1. 1) sin x > ![]() ; 2) tg x <
; 2) tg x < ![]() ;
;
2. ctg 2x < ![]() . 3. 2cos x ‑ 1
. 3. 2cos x ‑ 1 ![]() 0.
0.
Достатній рівень
Розв’язати нерівність:
1. 2cos ![]() . 2. 4sin 4x cos 4x >
. 2. 4sin 4x cos 4x > ![]() .
.
3. cos 5x cos x – sin 5x sin x < ![]() .
.
Високий рівень
Розв’язати нерівність:
1. 2sin2 x + sin x – 1 < 0. 2. sin x + sin 3x + sin 2x > 0.
3. 2cos2 ![]() >1.
>1.
№ 46. Варіант 2.
Середній рівень
Розв’язати нерівність:
1. 1) cos x > ‑![]() ; 2) ctg x <
; 2) ctg x < ![]() ;
;
2. tg ![]() < 1. 3. 2sin x +
< 1. 3. 2sin x + ![]() .
.
Достатній рівень
Розв’язати нерівність:
1. ![]() tg
tg ![]() . 2. sin x cos x <
. 2. sin x cos x < ![]() .
.
3. sin 2x sin 5x + cos 2x cos 5x > ![]() .
.
Високий рівень
Розв’язати нерівність:
1. 2cos2 x ‑ cos x – 1 < 0. 2. sin x + sin 3x ‑ sin 2x < 0.
3. tg2 x < 1.
№ 47. Варіант 3.
Середній рівень
Розв’язати нерівність:
1. 1) cos x < ![]() ; 2) ctg x > ‑1.
; 2) ctg x > ‑1.
2. sin 2x < ![]() . 3. 3tg x +
. 3. 3tg x + ![]()
![]() 0.
0.
Достатній рівень
Розв’язати нерівність:
1. ![]() sin
sin ![]() . 2. 2cos2
. 2. 2cos2 ![]() ‑ 1 <
‑ 1 < ![]() .
.
3. sin ![]() + cos
+ cos ![]() <
< ![]() .
.
Високий рівень
Розв’язати нерівність:
1. 2cos2 x ‑ 3sin x – 3 < 0. 2. cos x + cos 3x + cos 2x < 0.
3. ctg2 x < 3.
№ 48. Варіант 4.
Середній рівень
Розв’язати нерівність:
1. 1) sin x < ‑![]() ; 2) tg x < 1.
; 2) tg x < 1.
2. ctg 2x < ![]() . 3. 2cos x ‑
. 3. 2cos x ‑ ![]()
![]() 0.
0.
Достатній рівень
Розв’язати нерівність:
1. 2cos ![]() . 2. 1 ‑ 2sin2 2x >
. 2. 1 ‑ 2sin2 2x > ![]() .
.
3. ![]() sin x + cos x
sin x + cos x ![]() 0.
0.
Високий рівень
Розв’язати нерівність:
1. 2sin2 x + 5cos x – 4 < 0. 2. sin 4x ‑ sin 2x ‑ cos 3x > 0.
3. tg2 x > 1.
Тематичне оцінювання: теми 8 — 10
Контрольна робота 3
Варіант 1.
Середній рівень
1. 1) Розв’язати рівняння 2 cos x + ![]() .
.
2) Розв’язати нерівність sin 2x > ![]() .
.
Розв’язати рівняння (2 — 3):
2. tg2 x + 5tg x + 4 = 0. 3. sin 5x – sin x = 0.
Достатній рівень
1. 1) Розв’язати рівняння 2sin2 x + 3cos2 x + 2sin x = 0.
2) Розв’язати нерівність sin 3x cos x – cos 3x sin x > ![]() .
.
Розв’язати рівняння (2 — 3):
2. 2sin2 x – 4sin x cos x + 5cos2 x = 2. 3. sin x + cos x = ![]() .
.
Високий рівень
1. 1) Розв’язати рівняння cos x + cos 5x – 2cos 3x = 0.
2) Розв’язати нерівність 2sin2 x + sin x > 0.
2. Розв’язати рівняння sin2 6x + sin2 4x = 1.
3. Розв’язати систему рівнянь 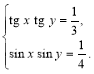
Варіант 2.
Середній рівень
1. 1) Розв’язати рівняння 2 sin x – 1 = 0.
2) Розв’язати нерівність tg 2x > 1.
Розв’язати рівняння (2 — 3):
2. sin2 x – 2sin x ‑ 3 = 0.
3. cos 3x + cos 5x = 0.
Достатній рівень
1. 1) Розв’язати рівняння 2cos2 x + 5sin x ‑ 4 = 0.
2) Розв’язати нерівність cos2 4x – sin2 4x ![]() .
.
Розв’язати рівняння (2 — 3):
2. 22cos2 x + 8sin x cos x = 7. 3. sin x + cos x = 1.
Високий рівень
1. 1) Розв’язати рівняння tg 2x ‑ ctg 3x = 0.
2) Розв’язати нерівність cos2 x + 2cos x < 0.
2. Розв’язати рівняння sin4 x + cos4 x = ![]() .
.
3. Розв’язати систему рівнянь 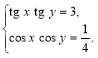
Варіант 3.
Середній рівень
1. 1) Розв’язати рівняння 2 sin x + 1 = 0.
2) Розв’язати нерівність cos 4x > ![]() .
.
Розв’язати рівняння (2 — 3):
2. ctg2 x – 2ctg x ‑ 3 = 0. 3. sin 3x + sin 5x = 0.
Достатній рівень
1. 1) Розв’язати рівняння 2cos 2x = 7cos x.
2) Розв’язати нерівність sin 3x cos x + cos 3x sin x ![]() .
.
Розв’язати рівняння (2 — 3):
2. 6sin2 x + 4sin x cos x + 4cos2 x = 3.
3. ![]() sin x ‑ cos x = 1.
sin x ‑ cos x = 1.
Високий рівень
1. 1) Розв’язати рівняння sin4![]() ‑ cos4
‑ cos4![]() =
= ![]() .
.
2) Розв’язати нерівність sin x + cos x < 1.
2. Розв’язати рівняння 2tg2 x + 4cos2 x = 7.
3. Розв’язати систему рівнянь 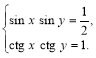
Варіант 4.
Середній рівень
1. 1) Розв’язати рівняння 2 sin x ‑ ![]() = 0.
= 0.
2) Розв’язати нерівність tg 4x > ![]() .
.
Розв’язати рівняння (2 — 3):
2. ctg2 x – 5ctg x + 4 = 0.
3. cos 2x ‑ cos 6x = 0.
Достатній рівень
1. 1) Розв’язати рівняння tg x + ctg x = 2.
2) Розв’язати нерівність sin 2x cos 2x ![]() .
.
Розв’язати рівняння (2 — 3):
2. 5sin2 x ‑ 5sin x cos x + 2cos2 x = 1.
3. sin x ‑ cos x = ![]() .
.
Високий рівень
1. 1) Розв’язати рівняння cos4 x ‑ sin4 x = ![]() .
.
2) Розв’язати нерівність sin x + cos x < ![]() .
.
2. Розв’язати рівняння cos 2x = 2tg2 x ‑ cos2 x.
3. Розв’язати систему рівнянь 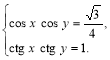
ІІІ. СТЕПЕНЕВА ФУНКЦІЯ
ТЕМА 11. КОРІНЬ n-ГО СТЕПЕНЯ
Самостійна робота № 1
Варіант 1.
Середній рівень
1. 1) Розв’язати рівняння:
а) x10 = 3; б) x8 = ‑5; в) x7 = 2; г) x5 = ‑3.
2) Обчислити:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Спростити вираз ![]() .
.
3. 1) Внести множник під знак кореня: а) 2![]() ; б)
; б) ![]()
2) Винести множник з-під знака корня: а) ![]() ; б)
; б) ![]() .
.
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Обчислити: ![]() .
.
3) Порівняти числа: 2![]() і 3
і 3![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3. Звільнитись від ірраціональності в знаменнику дробу:
а) ![]() ; б)
; б) ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Спростити вираз ![]() .
.
3) Порівняти числа ![]() і
і ![]() .
.
2. Виконати дії: ![]() .
.
3. Довести рівність ![]() .
.
Варіант 2.
Середній рівень
1. 1) Розв’язати рівняння:
а) x12 = 5; б) x11 = 7; в) x11 = ‑9; г) x10 = ‑7.
2) Обчислити:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Спростити вираз ![]() .
.
3. 1) Внести множник під знак кореня: а) 3![]() ; б)
; б) ![]()
2) Винести множник з-під знака корня: а) ![]() ; б)
; б) ![]() , де a > 0.
, де a > 0.
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Обчислити: ![]() .
.
3) Порівняти числа: 2![]() і 3
і 3![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3. Звільнитись від ірраціональності в знаменнику дробу:
а) ![]() ; б)
; б) ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Спростити вираз ![]() .
.
3) Порівняти числа ![]() і
і ![]() .
.
2. Довести рівність: ![]() .
.
3. Спростити вираз: 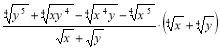 .
.
Варіант 3.
Середній рівень
1. 1) Розв’язати рівняння:
а) x6 = 2; б) x8 = ‑3; в) x7 = 4; г) x9 = ‑2.
2) Обчислити:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Спростити вираз ![]() .
.
3. 1) Внести множник під знак кореня: а) 5![]() ; б)
; б) ![]()
2) Винести множник з-під знака корня: а) ![]() ; б)
; б) ![]() .
.
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Обчислити: ![]() .
.
3) Порівняти числа: 2![]() і 3
і 3![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3. Звільнитись від ірраціональності в знаменнику дробу:
а) ![]() ; б)
; б) ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Спростити вираз ![]() .
.
3) Порівняти числа ![]() і
і ![]() .
.
2. Виконати дії: 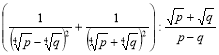 .
.
3. Довести подібність коренів: ![]() і
і ![]() .
.
Варіант 4.
Середній рівень
1. 1) Розв’язати рівняння:
а) x20 = 3; б) x18 = ‑4; в) x15 = 2; г) x13 = ‑7.
2) Обчислити:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
2. Спростити вираз ![]() .
.
3. 1) Внести множник під знак кореня: а) 2![]() ; б)
; б) ![]()
2) Винести множник з-під знака корня:
а) ![]() ; б)
; б) ![]() , де a > 0.
, де a > 0.
Достатній рівень
1. 1) Знайти область визначення функції:
а) ![]() ; б)
; б) ![]() .
.
2) Обчислити: ![]() .
.
3) Порівняти числа: 5![]() і 2
і 2![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3. Звільнитись від ірраціональності в знаменнику дробу:
а) ![]() ; б)
; б) ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції ![]() .
.
2) Спростити вираз ![]() .
.
3) Порівняти числа ![]() і
і ![]() .
.
2. Виконати дії: 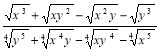 .
.
3. Довести подібність коренів: ![]() і
і ![]() .
.
ТЕМА 12. ІРРАЦІОНАЛЬНІ РІВНЯННЯ
Самостійна робота № 2
Варіант 1.
Середній рівень
Розв’язати рівняння:
1. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати рівняння (1 — 2):
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() .
.
3. Розв’язати систему рівнянь 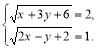 .
.
Високий рівень
1. 1) Розв’язати рівняння ![]() .
.
2) Розв’язати систему рівнянь 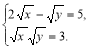 .
.
Розв’язати рівняння (2 — 3):
2. ![]() .
.
3. ![]() . Вказівка. Використати спосіб заміни змінної.
. Вказівка. Використати спосіб заміни змінної.
Варіант 2.
Середній рівень
Розв’язати рівняння:
1. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
2. ![]() .
.
3. ![]() .
.
Достатній рівень
Розв’язати рівняння (1 — 2):
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() .
.
3. Розв’язати систему рівнянь 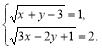 .
.
Високий рівень
1. 1) Розв’язати рівняння ![]() .
.
2) Розв’язати систему рівнянь 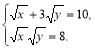 .
.
Розв’язати рівняння (2 — 3):
2. ![]() .
.
3. ![]() . Вказівка. Використати спосіб заміни змінної.
. Вказівка. Використати спосіб заміни змінної.
Варіант 3.
Середній рівень
Розв’язати рівняння:
1. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати рівняння (1 — 2):
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() .
.
3. Розв’язати систему рівнянь 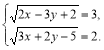 .
.
Високий рівень
1. 1) Розв’язати рівняння ![]() .
.
2) Розв’язати систему рівнянь ![]() .
.
Розв’язати рівняння (2 — 3):
2. ![]() .
.
3. ![]() . Вказівка. Використати спосіб заміни змінної.
. Вказівка. Використати спосіб заміни змінної.
Варіант 4.
Середній рівень
Розв’язати рівняння:
1. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати рівняння (1 — 2):
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() .
.
3. Розв’язати систему рівнянь 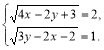 .
.
Високий рівень
1. 1) Розв’язати рівняння ![]() .
.
2) Розв’язати систему рівнянь ![]() .
.
Розв’язати рівняння (2 — 3):
2. ![]() .
.
3. ![]() . Вказівка. Використати спосіб заміни змінної.
. Вказівка. Використати спосіб заміни змінної.
ТЕМА 13. CТЕПІНЬ З РАЦІОНАЛЬНИМ ПОКАЗНИКОМ. СТЕПЕНЕВА ФУНКЦІЯ
Самостійна робота № 3
Варіант 1.
Середній рівень
1. 1) Подати у вигляді кореня:![]() ;
; ![]() .
.
2) Подати у вигляді степеня з дробовим показником: ![]() ;
; ![]() .
.
3) Обчислити:![]() ;
; ![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) 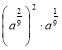 .
.
3. Накреслити ескіз графіка функції і записати її властивості:
а) y = x1,8; б) ![]() .
.
Достатній рівень
1. 1) Обчислити: ![]() .
.
2) Спростити вираз 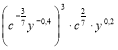 .
.
3) Накреслити ескіз графіка функції y = x0,8 + 2 і записати її властивості.
2. Розв’язати рівняння ![]() .
.
3. Спростити вираз ![]() .
.
Високий рівень
1. 1) Обчислити: ![]() .
.
2) Розв’язати рівняння ![]() .
.
3) Накреслити ескіз графіка функції ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа ![]() і
і ![]() .
.
3. Виконати дії: 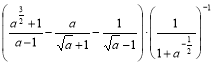 .
.
Варіант 2.
Середній рівень
1. 1) Подати у вигляді кореня:![]() ; 2)
; 2) ![]() .
.
2) Подати у вигляді степеня з дробовим показником: ![]() ;
;![]() .
.
3) Обчислити:![]() ;
; ![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) 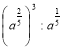 .
.
3. Накреслити ескіз графіка функції і записати її властивості:
а) y = x0,8; б) ![]() .
.
Достатній рівень
1. 1) Обчислити: ![]() .
.
2) Спростити вираз 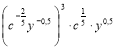 .
.
3) Накреслити ескіз графіка функції y = x‑0,5 + 3 і записати її властивості.
2. Розв’язати рівняння ![]() .
.
3. Спростити вираз ![]() .
.
Високий рівень
1. 1) Обчислити: ![]() .
.
2) Розв’язати рівняння ![]() .
.
3) Накреслити ескіз графіка функції ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа ![]() і
і ![]() .
.
3. Виконати дії: 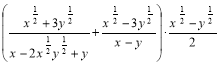 .
.
Варіант 3.
Середній рівень
1. 1) Подати у вигляді кореня:![]() ; 2)
; 2) ![]() .
.
2) Подати у вигляді степеня з дробовим показником: ![]() ;
;![]() .
.
3) Обчислити:![]() ;
; ![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) 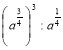 .
.
3. Накреслити ескіз графіка функції і записати її властивості:
а) y = x2,5; б) ![]() .
.
Достатній рівень
1. 1) Обчислити: ![]() .
.
2) Спростити вираз 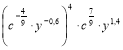 .
.
3) Накреслити ескіз графіка функції y = x0,7 + 3 і записати її властивості.
2. Розв’язати рівняння ![]() .
.
3. Спростити вираз 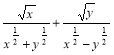 .
.
Високий рівень
1. 1) Обчислити: ![]() .
.
2) Розв’язати рівняння ![]() .
.
3) Накреслити ескіз графіка функції ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа ![]() і
і ![]() .
.
3. Виконати дії: 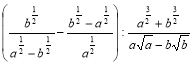 .
.
Варіант 4.
Середній рівень
1. 1) Подати у вигляді кореня:![]() ; 2)
; 2) ![]() .
.
2) Подати у вигляді степеня з дробовим показником: ![]() ;
;![]() .
.
3) Обчислити:![]() ;
; ![]() .
.
2. Спростити вираз: а) ![]() ; б)
; б) 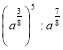 .
.
3. Накреслити ескіз графіка функції і записати її властивості:
а) y = x0,4; б) ![]() .
.
Достатній рівень
1. 1) Обчислити: ![]() .
.
2) Спростити вираз 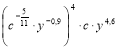 .
.
3) Накреслити ескіз графіка функції y = x1,4 + 3 і записати її властивості.
2. Розв’язати рівняння ![]() .
.
3. Спростити вираз 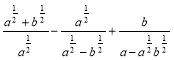 .
.
Високий рівень
1. 1) Обчислити: ![]() .
.
2) Розв’язати рівняння ![]() .
.
3) Накреслити ескіз графіка функції ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа ![]() і
і ![]() .
.
3. Виконати дії: 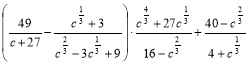 .
.
Тематичне оцінювання: теми 11 — 13
Контрольна робота 4
Варіант 1.
Середній рівень
1. 1) Подати у вигляді степеня: ![]() ;
; ![]() .
.
2) Обчислити:![]() ;
; ![]() .
.
3) Знайти область визначення функції:
а) y = x21; б) y = x‑5; в) y = x‑0,4; г) y = 0,4.
2. Спростити вираз: 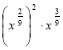 ;
; ![]() .
.
3. 1) Розв’язати рівняння ![]() .
.
2) Накреслити ескіз графіка функції: а) y = x20; б) ![]() .
.
Достатній рівень
1. 1) Знайти область визначення функції:
а) y = (2x – 1)0,5; б) y = (3x + 2)‑1,2.
2) Подати у вигляді степеня вираз ![]() .
.
3) Накреслити ескіз графіка функції y = x‑2,3 + 1.
2. Спростити вираз ![]() .
.
3. Розв’язати рівняння ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції y = (2x – 5)0,1 + (3 – x)‑0,1.
2) Спростити вираз: 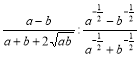 .
.
3) Розв’язати рівняння ![]() .
.
2. Порівняти числа: а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() .
.
3. Накреслити ескіз графіка функції ![]() .
.
Варіант 2.
Середній рівень
1. 1) Подати у вигляді степеня: ![]() ;
; ![]() .
.
2) Обчислити:![]() ;
; ![]() .
.
3) Знайти область визначення функції:
а) y = x2,3; б) y = x23; в) y = ![]() ; г) y = x7.
; г) y = x7.
2. Спростити вираз: 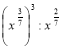 ;
; ![]() .
.
3. 1) Розв’язати рівняння ![]() .
.
2) Накреслити ескіз графіка функції: а) y = x‑20; б) ![]() .
.
Достатній рівень
1. 1) Знайти область визначення функції: а) y = (4x + 3)1,4; б) y = ![]() .
.
2) Подати у вигляді степеня вираз ![]() .
.
3) Накреслити ескіз графіка функції y = x0,7 + 2.
2. Спростити вираз ![]() .
.
3. Розв’язати рівняння ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції: y = ![]() .
.
2) Спростити вираз: 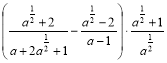 .
.
3) Розв’язати рівняння ![]() .
.
2. Порівняти числа: а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() .
.
3. Накреслити ескіз графіка функції ![]() .
.
Варіант 3.
Середній рівень
1. 1) Подати у вигляді степеня: ![]() ;
; ![]() .
.
2) Обчислити:![]() ;
; ![]() .
.
3) Знайти область визначення функції:
а) y = x14; б) y = x‑14; в) y = ![]() ; г) y = x‑1,4.
; г) y = x‑1,4.
2. Спростити вираз: 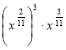 ;
; ![]() .
.
3. 1) Розв’язати рівняння ![]() .
.
2) Накреслити ескіз графіка функції:
а) y = x21; б) ![]() .
.
Достатній рівень
1. 1) Знайти область визначення функції:
а) y = (5x ‑ 2)1,3; б) y = ![]() .
.
2) Подати у вигляді степеня вираз ![]() .
.
3) Накреслити ескіз графіка функції y = x0,7 + 2.
2. Спростити вираз 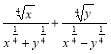 .
.
3. Розв’язати рівняння ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції: y = ![]() .
.
2) Спростити вираз: ![]() .
.
3) Розв’язати рівняння ![]() .
.
2. Порівняти числа: а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() .
.
3. Накреслити ескіз графіка функції ![]() .
.
Варіант 4.
Середній рівень
1. 1) Подати у вигляді степеня: ![]() ;
; ![]() .
.
2) Обчислити:![]() ;
; ![]() .
.
3) Знайти область визначення функції:
а) y = x8; б) y = x‑8; в) y = ![]() ; г) y =
; г) y = ![]() .
.
2. Спростити вираз: 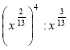 ;
; ![]() .
.
3. 1) Розв’язати рівняння ![]() .
.
2) Накреслити ескіз графіка функції:
а) y = x0,8; б) ![]() .
.
Достатній рівень
1. 1) Знайти область визначення функції:
а) y = (6 ‑ x)2,5; б) y = ![]() .
.
2) Подати у вигляді степеня вираз ![]() .
.
3) Накреслити ескіз графіка функції y = x0,2 ‑ 3.
2. Спростити вираз 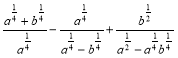 .
.
3. Розв’язати рівняння ![]() .
.
Високий рівень
1. 1) Знайти область визначення функції: y = ![]() .
.
2) Спростити вираз: 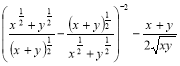 .
.
3) Розв’язати рівняння ![]() .
.
2. Порівняти числа:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() .
.
3. Накреслити ескіз графіка функції ![]() .
.
ІV. ПОКАЗНИКОВА І ЛОГАРИФМІЧНА ФУНКЦІЯ
ТЕМА 14. ПОКАЗНИКОВА ФУНКЦІЯ
Самостійна робота № 1
Варіант 1.
Середній рівень
1. Побудувати графік функції y = 3х і записати її властивості.
2. Порівняти числа: а) 50,4 і 50,7; б) ![]() і
і ![]() .
.
3. Знайти область значень функції: а) y = 7x + 5; б) ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = 5x + 2 і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) a7 < a9; б) a10 < a5.
2. Знайти найбільше і найменше значення функції y = 2x, якщо ![]() .
.
3. Розв’язати графічно рівняння ![]() .
.
Високий рівень
1. 1) Розв’язати графічно рівняння ![]() .
.
2) Порівняти числа: а) ![]() і 1; б)
і 1; б) ![]() і 1.
і 1.
2. Знайти найбільше і найменше значення функції y = ![]()
3. Побудувати графік функції y = 3|x| і записати її властивості.
Варіант 2.
Середній рівень
1. Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа: а) 70,9 і 71,2; б) ![]() і
і ![]() .
.
3. Знайти область значень функції: а) y = 4x ‑ 3; б) ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = 2x ‑ 3 і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) a14 < a19; б) a7 < a3.
2. Знайти найбільше і найменше значення функції y = 3x, якщо ![]() .
.
3. Розв’язати графічно рівняння ![]() .
.
Високий рівень
1. 1) Розв’язати графічно рівняння ![]() .
.
2) Порівняти числа: а) ![]() і 1; б)
і 1; б) ![]() і 1.
і 1.
2. Знайти найбільше і найменше значення функції y = 3sin x.
3. Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
Варіант 3.
Середній рівень
1. Побудувати графік функції y = 5х і записати її властивості.
2. Порівняти числа: а) 6‑0,8 і 6‑0,1; б) ![]() і
і ![]() .
.
3. Знайти область значень функції: а) y = 0,8x + 3; б) y = 9,1x ‑ 6.
Достатній рівень
1. 1) Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) a2,3 > a3,1; б) a‑4 < a‑1,4.
2. Знайти найбільше і найменше значення функції y = ![]() , якщо
, якщо ![]() .
.
3. Розв’язати графічно рівняння ![]() .
.
Високий рівень
1. 1) Розв’язати графічно рівняння ![]() .
.
2) Порівняти числа: а) ![]() і 1; б)
і 1; б) ![]() і 1.
і 1.
2. Знайти найбільше і найменше значення функції y = ![]()
3. Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
Варіант 4.
Середній рівень
1. Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа: а) 7,10,5 і 7,10,2; б) 0,70,9 і 0,70,3.
3. Знайти область значень функції: а) y = 0,7x ‑ 4; б) ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) ![]() ; б) a < a4.
; б) a < a4.
2. Знайти найбільше і найменше значення функції y = 5x, якщо ![]() .
.
3. Розв’язати графічно рівняння ![]() .
.
Високий рівень
1. 1) Розв’язати графічно рівняння ![]() .
.
2) Порівняти числа: а) ![]() і 1; б)
і 1; б) ![]() і 1.
і 1.
2. Знайти найбільше і найменше значення функції y = 5cos x – 2.
3. Побудувати графік функції y = 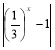 і записати її властивості.
і записати її властивості.
ТЕМА 15. ПОКАЗНИКОВІ РІВНЯННЯ
Самостійна робота № 2
Варіант 1.
Середній рівень
Розв’язати рівняння:
1. 1) ![]() ; 2) 5x – 1 – 1 = 0.
; 2) 5x – 1 – 1 = 0.
2. 3x + 1 + 3x = 108. 3. 4x – 3 2x + 2 = 0.
Достатній рівень
Розв’язати рівняння:
1. 1) 4x + 1 – 4x – 4x – 1 = 44; 2) 2x + 1 + 4x = 80.
2. ![]() .
.
3. Розв’язати систему рівнянь ![]() .
.
Високий рівень
Розв’язати рівняння:
1. 1) 2 4x + 1 – 3x = 3x + 2 – 2 4x; 2) 4 9x + 12x = 3 16x.
2. Розв’язати систему рівнянь ![]() .
.
3. Розв’язати рівняння ![]() .
.
Варіант 2.
Середній рівень
Розв’язати рівняння:
1. 1) 24x = 64; 2) ![]() .
.
2. 5x + 2 + 5x = 130. 3. 9x – 4 3x + 3 = 0.
Достатній рівень
Розв’язати рівняння:
1. 1) 5x + 1 – 5x + 5x – 1 = 105; 2) 3x + 1 + 9x = 108.
2. ![]() .
.
3. Розв’язати систему рівнянь ![]() .
.
Високий рівень
Розв’язати рівняння:
1. 1) 6x + 6x + 1 = 2x + 2x + 1 + 2x + 2; 2) 2 4x – 3 10x = 5 25x.
2. Розв’язати систему рівнянь ![]() .
.
3. Розв’язати рівняння ![]() .
.
Варіант 3.
Середній рівень
Розв’язати рівняння:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. 2x + 2 + 2x = 40.
3. ![]() .
.
Достатній рівень
Розв’язати рівняння:
1. 1) 5x + 1 + 3 5x ‑ 1 – 6 5x + 10 = 0; 2) 22x + 1 – 7 2x + 3 = 0.
2. ![]() .
.
3. Розв’язати систему рівнянь ![]() .
.
Високий рівень
Розв’язати рівняння:
1. 1) 2x + 2x + 1 + 2x + 2 = 2 5x + 5x + 1; 2) 4x + 6x = 2 9x.
2. Розв’язати систему рівнянь ![]() .
.
3. Розв’язати рівняння ![]() .
.
Варіант 4.
Середній рівень
Розв’язати рівняння:
1. 1) ![]() ; 2) 43x ‑ 1 – 1 = 0.
; 2) 43x ‑ 1 – 1 = 0.
2. 2x + 1 + 2x = 48. 3. 4x – 5 2x + 4 = 0.
Достатній рівень
Розв’язати рівняння:
1. 1) 2 3x ‑ 6 + 6 90,5x ‑ 2 = 56; 2) 9x – 5 3x + 1 + 54 = 0.
2. ![]() .
.
3. Розв’язати систему рівнянь 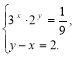 .
.
Високий рівень
Розв’язати рівняння:
1. 1) 2 3x ‑ 1 – 3x ‑ 2 = 5x ‑ 2 + 4 5x ‑ 3; 2) 8x + 18x = 2 27x.
2. Розв’язати систему рівнянь ![]() .
.
3. Розв’язати рівняння ![]() .
.
ТЕМА 16. ПОКАЗНИКОВІ НЕРІВНОСТІ
Самостійна робота № 3
Варіант 1.
Середній рівень
Розв’язати нерівність:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. 53x ‑ 1 < 25. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 2x + 1 + 2x > 24; 2) ![]() .
.
2. 4x – 6 2x + 8 < 0.
3. Розв’язати графічно нерівність 2x > 3 ‑ x.
Високий рівень
Розв’язати нерівність:
1. 1) x2 3x – 3x + 1 ![]() ; 2) 4x 5 + 2 25x
; 2) 4x 5 + 2 25x ![]() .
.
2. ![]() .
.
3. Розв’язати графічно нерівність ![]() .
.
Варіант 2.
Середній рівень
Розв’язати нерівність:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 3x + 2 + 3x ‑ 1 > 28; 2) ![]() .
.
2. 4x – 2x < 12.
3. Розв’язати графічно нерівність ![]() .
.
Високий рівень
Розв’язати нерівність:
1. 1) 22 + x ‑ 2x + 3 – 2x + 4 > 5x + 1 – 5x + 2; 2) 2x + 23 ‑ x <9;.
2. ![]() .
.
3. Розв’язати графічно нерівність ![]() .
.
Варіант 3.
Середній рівень
Розв’язати нерівність:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. 102x + 1 < 0,1. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 3x + 2 + 3x < 30; 2) ![]() .
.
2. ![]() .
.
3. Розв’язати графічно нерівність ![]() .
.
Високий рівень
Розв’язати нерівність:
1. 1) x2 0,2x – 0,2x + 2 < 0; 2) 3x + 32 ‑ x > 10.
2. ![]() .
.
3. Розв’язати графічно нерівність ![]() .
.
Варіант 4.
Середній рівень
Розв’язати нерівність:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. 103x + 1 > 0,001. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність (1 — 2):
1. 1) 5x + 1 – 3 5x ‑ 2 < 122; 2) ![]() .
.
2. 3 9x + 11 3x < 4.
3. Розв’язати графічно нерівність ![]() .
.
Високий рівень
Розв’язати нерівність:
1. 1) ![]() ; 2) 22 + x + 22 ‑ x > 15.
; 2) 22 + x + 22 ‑ x > 15.
2. ![]() .
.
3. Розв’язати графічно нерівність ![]() .
.
Тематичне оцінювання: теми 14 — 16
Контрольна робота 5
Варіант 1.
Середній рівень
1. 1) Побудувати графік функції y = 4x і записати її властивості.
2) Розв’язати рівняння ![]() .
.
Розв’язати нерівність:
3) ![]() ; 4)
; 4) ![]() .
.
Розв’язати рівняння (2 — 3):
2. 7x + 2 – 7x = 42.
3. 25x – 6 5x + 5 = 0.
Достатній рівень
1. 1) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння 4x + 2x + 1 = 80.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати нерівність ![]() .
.
3. Розв’язати систему рівнянь ![]()
Високий рівень
1. 1) Побудувати графік функції y = 2x ‑ 3 – 1.
2) Розв’язати рівняння 7 49x + 5 14x = 2 4x.
3) Розв’язати нерівність 2x – 23 – x > 2
2. Розв’язати систему рівнянь ![]() .
.
3. Побудувати графік функції y = 0,5|x|.
Варіант 2.
Середній рівень
1. 1) Побудувати графік функції y = 4x і записати її властивості.
2) Розв’язати рівняння ![]() .
.
Розв’язати нерівність:
3) ![]() ; 4)
; 4) ![]() .
.
Розв’язати рівняння (2 — 3):
2. 3x + 2 + 3x = 270.
3. 4x – 9 2x + 8 = 0.
Достатній рівень
1. 1) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння 22x + 1 + 2x + 2 = 16.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати нерівність ![]() .
.
3. Розв’язати систему рівнянь ![]()
Високий рівень
1. 1) Побудувати графік функції y = 2x + 4 – 1.
2) Розв’язати рівняння 3 9x = 2 15x + 5 25x.
3) Розв’язати нерівність 31 + x + 32 – x < 28.
2. Розв’язати систему рівнянь 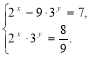 .
.
3. Побудувати графік функції ![]() .
.
Варіант 3.
Середній рівень
1. 1) Побудувати графік функції y = 5x і записати її властивості.
2) Розв’язати рівняння 7x + 4 – 1 = 0.
Розв’язати нерівність:
3) 25x ‑ 1 < 32; 4) ![]() .
.
Розв’язати рівняння (2 — 3):
2. 5x + 2 – 5x = 120.
3. 9x – 10 3x + 9 = 0.
Достатній рівень
1. 1) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння 3x + 2 + 9x + 1 – 810 = 0.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати нерівність ![]() .
.
3. Розв’язати систему рівнянь ![]()
Високий рівень
1. 1) Побудувати графік функції ![]() .
.
2) Розв’язати рівняння 2 25x ‑ 5 10x + 2 4x = 0
3) Розв’язати нерівність 5x – 51 – x < 4.
2. Розв’язати систему рівнянь 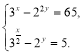 .
.
3. Побудувати графік функції y = 4|x|.
Варіант 4.
Середній рівень
1. 1) Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння 92x ‑ 1 – 1 = 0.
Розв’язати нерівність:
3) 103x ‑ 1 > 100000; 4) ![]() .
.
Розв’язати рівняння (2 — 3):
2. 2x + 3 + 2x = 36.
3. 9x – 7 3x ‑ 18 = 0.
Достатній рівень
1. 1) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння 3x + 2 + 9x + 1 – 108 = 0.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати нерівність ![]() .
.
3. Розв’язати систему рівнянь 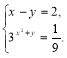
Високий рівень
1. 1) Побудувати графік функції ![]() .
.
2) Розв’язати рівняння 2 4x ‑ 5 6x + 3 9x = 0
3) Розв’язати нерівність 5‑x – 5 x + 2 > 24.
2. Розв’язати систему рівнянь ![]() .
.
3. Побудувати графік функції y = 5|x|.
ТЕМА 17. ЛОГАРИФМ ЧИСЛА
Самостійна робота № 1
Варіант 1.
Середній рівень
1. Обчислити:
1) log2 64; ![]() ;
; ![]() ;
;
2) log6 2 + log6 3; ![]() ;
; ![]() ; 3)
; 3) ![]() .
.
2. Прологарифмувати за основою 5 вираз ![]() .
.
3. Знайти lg x = lg 12 + 5lg a + ![]() lg b – 4lg c.
lg b – 4lg c.
Достатній рівень
1. 1) Обчислити: ![]() ;
; ![]() ;
; ![]() .
.
2) Прологарифмувати за основою 3 вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. log2 3 = a; log2 5 = b. Знайти: log2 15; log2 6; log2 75; log3 5.
3. Використовуючи формулу переходу до нової основи логарифма, довести, що ![]() .
.
Високий рівень
1. 1) Обчислити: ![]() ;
; ![]() .
.
2) Прологарифмувати за основою 10 вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. Обчислити log4 5 log5 6 log6 7 log7 8.
3. Довести тотожність ![]() .
.
Варіант 2.
Середній рівень
1. Обчислити:
1) log3 81; ![]() ;
; ![]() ;
;
2) log21 3 + log21 7; ![]() ;
; ![]() ;
;
3) ![]() .
.
2. Прологарифмувати за основою 7 вираз ![]() .
.
3. Знайти lg x = lg 2 + 3lg a + 2lg b – ![]() lg c.
lg c.
Достатній рівень
1. 1) Обчислити: ![]() ;
; ![]() ;
; ![]() .
.
2) Прологарифмувати за основою 5 вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. log7 2 = a; log7 3 = b. Знайти: log7 6; log7 ![]() ; log7 18; log3 2.
; log7 18; log3 2.
3. Використовуючи формулу переходу до нової основи логарифма, довести, що ![]() .
.
Високий рівень
1. 1) Обчислити: ![]() ;
; ![]() .
.
2) Прологарифмувати за основою вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. Обчислити log3 49 ![]() log25 27.
log25 27.
3. Довести тотожність ![]() .
.
Варіант 3.
Середній рівень
1. Обчислити:
1) log5 125; ![]() ;
; ![]() ;
;
2) log12 2 + log12 72; ![]() ;
; ![]() ; 3)
; 3) ![]() .
.
2. Прологарифмувати за основою 3 вираз ![]() .
.
3. Знайти lg x = lg 2 + 3lg a + ![]() lg с – lg b.
lg с – lg b.
Достатній рівень
1. 1) Обчислити: ![]() ;
; ![]() ;
; ![]() .
.
2) Прологарифмувати за основою 2 вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. log3 2 = a; log3 7 = b. Знайти: log3 14; log3 6; log3 28; log2 7.
3. Використовуючи формулу переходу до нової основи логарифма, довести, що ![]() .
.
Високий рівень
1. 1) Обчислити: ![]() ;
; ![]() .
.
2) Прологарифмувати за основою 3 вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. Обчислити log8 9, якщо log12 18 = a.
3. Довести тотожність ![]() .
.
Варіант 4.
Середній рівень
1. Обчислити:
1) ![]() ;
; ![]() ;
; ![]() ;
;
2) log3 6 + log3 ![]() ;
; ![]() ;
; ![]() ; 3)
; 3) ![]() .
.
2. Прологарифмувати за основою 2 вираз ![]() .
.
3. Знайти lg x = lg 5 + 2lg a ‑ ![]() lg b + lg c.
lg b + lg c.
Достатній рівень
1. 1) Обчислити: ![]() ;
; ![]() ;
; ![]() .
.
2) Прологарифмувати за основою 10 вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. log5 2 = a; log5 3 = b. Знайти: log5 6; log5 ![]() ; log5 12; log2 3.
; log5 12; log2 3.
3. Використовуючи формулу переходу до нової основи логарифма, довести, що ![]() .
.
Високий рівень
1. 1) Обчислити: ![]() ;
; ![]() .
.
2) Прологарифмувати за основою 2 вираз ![]() .
.
3) Знайти x, якщо ![]() .
.
2. Обчислити log6 16, якщо log12 2 = a.
3. Довести тотожність ![]() .
.
ТЕМА 18. ЛОГАРИФМІЧНА ФУНКЦІЯ
Самостійна робота № 2
Варіант 1.
Середній рівень
1. Побудувати графік функції y = log3 x і записати її властивості.
2. Порівняти числа: а) log3 5,4 і log3 6,2; б) ![]() і
і ![]() .
.
3. Знайти область визначення функції y = log0,4 (3x – 1).
Достатній рівень
1. 1) Побудувати графік функції y = log2 (x + 1) і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) loga 7 < loga 5; б) loga 7,1 > loga 5,9.
2. Знайти область визначення функції y = log2 sin x.
3. Розв’язати графічно рівняння log0,5 x = 2x – 5.
Високий рівень
1. 1) Побудувати графік функції ![]() .
.
2) Порівняти числа: а) log0,4 7 і 0; б) log9 1,3 і 0.
2. Знайти область визначення функції ![]() .
.
3. Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
Варіант 2.
Середній рівень
1. Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа: а) log11 0,7 і log11 0,6; б) ![]() і
і ![]() .
.
3. Знайти область визначення функції y = log7 (5x + 3).
Достатній рівень
1. 1) Побудувати графік функції y = log0,5 (x + 1) і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) loga 1,2 < loga 2,2; б) loga 0,3 > loga 0,5.
2. Знайти область визначення функції y = log0,4 cos x.
3. Розв’язати графічно рівняння log2 x = ‑x + 1.
Високий рівень
1. 1) Побудувати графік функції ![]() .
.
2) Порівняти числа: а) 0 і log0,4 0,5; б) 0 і log7 1,2.
2. Знайти область визначення функції ![]() .
.
3. Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
Варіант 3.
Середній рівень
1. Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа: а) log7,1 3,7 і log7,1 3,9; б) ![]() і
і ![]() .
.
3. Знайти область визначення функції ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = log2 (x ‑ 2) і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) loga < loga 4; б) loga > loga 3.
2. Знайти область визначення функції ![]() .
.
3. Розв’язати графічно рівняння log2 x = x ‑ 4.
Високий рівень
1. 1) Побудувати графік функції ![]() .
.
2) Порівняти числа: а) log 0,8 і 0; б) ![]() і 0.
і 0.
2. Знайти область визначення функції ![]() .
.
3. Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
Варіант 4.
Середній рівень
1. Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2. Порівняти числа: а) log1,1 0,3 і log1,1 0,5; б) ![]() і
і ![]() .
.
3. Знайти область визначення функції ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = log3 (x + 1) і записати її властивості.
2) Порівняти основу a > 0 з одиницею, якщо:
а) loga 0,6 < loga 0,5; б) loga 5,9 > loga 5,7.
2. Знайти область визначення функції ![]() .
.
3. Розв’язати графічно рівняння ![]() .
.
Високий рівень
1. 1) Побудувати графік функції ![]() .
.
2) Порівняти числа: а) log0,7 5 і 0; б) ![]() і 0.
і 0.
2. Знайти область визначення функції ![]() .
.
3. Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
ТЕМА 19. ЛОГАРИФМІЧНІ РІВНЯННЯ
Самостійна робота № 4
Варіант 1.
Середній рівень
Розв’язати рівняння:
1. 1) 2x = 3; 2) log4 (5x + 1) = 2; 3) log2 (2x + 1) = log2 (x – 2).
2. log2 x + log2 (x + 6) = 4.
3. ![]() .
.
Достатній рівень
Розв’язати рівняння:
1. 1) lg (3x – 1) – lg (x + 5) = lg 5; 2) 3lg2 (x ‑ 1) – 10lg (x – 1) + 3 = 0.
2. log7 log3 log2 x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
Розв’язати рівняння:
1. 1) log2 x + logx 2 = ![]() ; 2)
; 2) ![]() . 2.
. 2. ![]() .
.
3. Розв’язати систему рівнянь ![]()
Варіант 2.
Середній рівень
Розв’язати рівняння:
1. 1) 7x = 2; 2) log3 (5x ‑ 1) = 2; 3) log2 (x ‑ 7) = log2 (11 ‑ x).
2. log3 (x + 1) + log3 (x + 3) = 1.
3. ![]() .
.
Достатній рівень
Розв’язати рівняння:
1. 1) lg (x – 1) – lg (2x ‑ 11) = lg 2; 2) ![]() .
.
2. log2 log3 log4 x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
Розв’язати рівняння:
1. 1) 2logx 27 ‑ 3log27 x = 1; 2) ![]() .
.
2. 0,1xlg x – 2 = 100.
3. Розв’язати систему рівнянь ![]()
Варіант 3.
Середній рівень
Розв’язати рівняння:
1. 1) 5x = 4; 2) log2 (3x ‑ 1) = 3; 3) log5 (x + 1) = log5 (7 ‑ x).
2. log5 (x + 1) + log5 (2x + 3) = 0. 3. ![]() .
.
Достатній рівень
Розв’язати рівняння:
1. 1) lg (x + 6) – ![]() lg (2x ‑ 3) = 2 ‑ lg 25; 2)
lg (2x ‑ 3) = 2 ‑ lg 25; 2) ![]() .
.
2. log5 log3 log2 log2 x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
Розв’язати рівняння:
1. 1) log3 x ‑ ![]() ; 2) log2 x + log4 x + log16 x = 7.
; 2) log2 x + log4 x + log16 x = 7.
2. ![]() .
.
3. Розв’язати систему рівнянь ![]()
Варіант 4.
Середній рівень
Розв’язати рівняння:
1. 1) 9x = 5; 2) log4 (5x + 1) = 2; 3) log0,3 (13 ‑ x) = log0,3 (x + 3).
2. lg (x ‑ 3) + lg (x + 6) = lg 2 + lg 5. 3. ![]() .
.
Достатній рівень
Розв’язати рівняння:
1. 1) log2 (3x ‑ 1) + log2 (x ‑ 1) = 1 + log2 (x + 5); 2) ![]() .
.
2. lg lg lg x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
Розв’язати рівняння:
1. 1) logx 10 +lg x = 2; 2) log3 x log9 x log27 x log81 x = ![]() .
.
2. ![]() .
.
3. Розв’язати систему рівнянь ![]()
ТЕМА 20. ЛОГАРИФМІЧНІ НЕРІВНОСТІ
Самостійна робота № 5
Варіант 1.
Середній рівень
Розв’язати нерівність:
1. 1) log5 x > 2; 2) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність:
1. 1) log2 (x2 – 13x + 30) > 3; 2) ![]() .
.
2. ![]() . 3. logx (x + 2) > 0.
. 3. logx (x + 2) > 0.
Високий рівень
Розв’язати нерівність:
1. 1) log0,4 (x2 + 2x – 3) > log0,4 (x – 1); 2) log3 – x (x – 2,5) > 0.
2. xlg x < 100x. 3. ![]() .
.
Варіант 2.
Середній рівень
Розв’язати нерівність:
1. 1) log6 x > 2; 2) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() .
.
3. logx (x + 3) > 0.
Високий рівень
Розв’язати нерівність:
1. 1) log0,7 (x2 ‑ 2x – 3) log0,8 (9 ‑ x); 2) log2x + 3 x2 < 1.
2. xlg x < 1000x2.
3. ![]() .
.
Варіант 3.
Середній рівень
Розв’язати нерівність:
1. 1) log5 x > ‑2; 2) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() . 3. logx (3x ‑ 1) > 1.
. 3. logx (3x ‑ 1) > 1.
Високий рівень
Розв’язати нерівність:
1. 1) log0,2 (x + 1) + log0,3 (5 ‑ x) log0,2 (x + 7); 2) log0,5 log8 ![]() < 0.
< 0.
2. ![]() .
.
3. ![]() .
.
Варіант 4.
Середній рівень
Розв’язати нерівність:
1. 1) log2 x > 3; 2) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Достатній рівень
Розв’язати нерівність:
1. 1) ![]() ; 2)
; 2) ![]() .
.
2. ![]() . 3. log4 (5x ‑ 1) > 1.
. 3. log4 (5x ‑ 1) > 1.
Високий рівень
Розв’язати нерівність:
1. 1) log0,8 (x + 2) + log0,8 (6 ‑ x) log0,8 (x + 8); 2) ![]() .
.
2. ![]() . 3.
. 3. ![]() .
.
Тематичне оцінювання: теми 17 — 20
Контрольна робота 6
Варіант 1.
Середній рівень
1. 1) Побудувати графік функції y = log2 x і записати її властивості.
2) Розв’язати рівняння log2 (3x + 1) = 4.
2. Розв’язати рівняння log2 x + log2 (x + 2) = 3.
3. Розв’язати нерівність ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2) Прологарифмувати за основою 4 вираз ![]() .
.
3) Розв’язати нерівність lg (3x + 4) < lg 2x.
2. Розв’язати рівняння log5 log3 log2 x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
1. 1) Побудувати графік функції y = 1 + log3 (x ‑ 1).
2) Розв’язати рівняння log2 x – 2logx 2 = ‑1.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати рівняння xlg x = 1000x2.
3. Розв’язати систему рівнянь ![]() .
.
Варіант 2.
Середній рівень
1. 1) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння log5 (2x ‑ 1) = 3.
2. Розв’язати рівняння ![]() .
.
3. Розв’язати нерівність ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2) Прологарифмувати за основою ![]() вираз
вираз ![]() .
.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати рівняння lg log3 log4 x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
1. 1) Побудувати графік функції y = ‑1 + ![]() .
.
2) Розв’язати рівняння log2 x + logx 2 = 2,5.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати рівняння ![]() .
.
3. Розв’язати систему рівнянь ![]() .
.
Варіант 3.
Середній рівень
1. 1) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння lg (3x + 1) = 2.
2. Розв’язати рівняння ![]() .
.
3. Розв’язати нерівність ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2) Прологарифмувати за основою 2 вираз ![]() .
.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати рівняння log2 log3 lg x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
1. 1) Побудувати графік функції y = 2 + ![]() .
.
2) Розв’язати рівняння log3 x = 1 + logx 9.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати рівняння ![]() .
.
3. Розв’язати систему рівнянь ![]() .
.
Варіант 4.
Середній рівень
1. 1) Побудувати графік функції ![]() і записати її властивості.
і записати її властивості.
2) Розв’язати рівняння log3 (4x + 1) = 2.
2. Розв’язати рівняння ![]() .
.
3. Розв’язати нерівність ![]() .
.
Достатній рівень
1. 1) Побудувати графік функції y = ![]() і записати її властивості.
і записати її властивості.
2) Прологарифмувати за основою 2 вираз ![]() .
.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати рівняння log8 log9 lg x = 0.
3. Розв’язати систему рівнянь ![]()
Високий рівень
1. 1) Побудувати графік функції y = ![]() .
.
2) Розв’язати рівняння log3 x + 2logx 3 = 3.
3) Розв’язати нерівність ![]() .
.
2. Розв’язати рівняння ![]() .
.
3. Розв’язати систему рівнянь ![]()
1
-
Дякую за розробку!

про публікацію авторської розробки
Додати розробку
