Самостійні роботи з геометрії 8 клас
Архів містить самостійні роботи з математики у 2 варіантах по дві самостійні роботи з кожної теми. Роздруковуються на обох сторонах аркуша, розрізаються та роздаються по одному на парту.
Тема 1 сам. роб. № 1
Варіант 1
- Один з кутів паралелограма дорівнює 470. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 112 см, а дві його сторони відносяться як 5:3. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 8 см.
Тема 1 сам. роб. № 1
Варіант 1
- Один з кутів паралелограма дорівнює 470. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 112 см, а дві його сторони відносяться як 5:3. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 8 см.
Тема 1 сам. роб. № 1
Варіант 1
- Один з кутів паралелограма дорівнює 470. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 112 см, а дві його сторони відносяться як 5:3. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 8 см.
Тема 1 сам. роб. № 1
Варіант 1
- Один з кутів паралелограма дорівнює 470. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 112 см, а дві його сторони відносяться як 5:3. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 8 см.
Тема 1 сам. роб. № 1
Варіант 2
- Один з кутів паралелограма дорівнює 1320. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 48 см, а одна з його сторін в 3 рази більше від іншої. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 12 см.
Тема 1 сам. роб. № 1
Варіант 2
- Один з кутів паралелограма дорівнює 1320. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 48 см, а одна з його сторін в 3 рази більше від іншої. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 12 см.
Тема 1 сам. роб. № 1
Варіант 2
- Один з кутів паралелограма дорівнює 1320. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 48 см, а одна з його сторін в 3 рази більше від іншої. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 12 см.
Тема 1 сам. роб. № 1
Варіант 2
- Один з кутів паралелограма дорівнює 1320. Знайдіть решту кутів.
- Периметр паралелограма дорівнює 48 см, а одна з його сторін в 3 рази більше від іншої. Знайдіть сторони паралелограма.
- Бісектриса одного з кутів паралелограма ділить його сторону навпіл. Знайдіть периметр паралелограма, якщо ця сторона дорівнює 12 см.
Тема 1 сам. роб. № 2
Варіант 1
- Кут між діагоналлю і стороною ромба дорівнює 200. Знайдіть кути ромба.
- Периметр прямокутника дорівнює 36 см. Знайдіть сторони прямокутника, якщо одна з них у 2 рази менша від другої.
-
О – точка перетину діагоналей прямокутника АВСD.
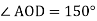
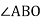
Тема 1 сам. роб. № 1
Варіант 1
- Кут між діагоналлю і стороною ромба дорівнює 200. Знайдіть кути ромба.
- Периметр прямокутника дорівнює 36 см. Знайдіть сторони прямокутника, якщо одна з них у 2 рази менша від другої.
-
О – точка перетину діагоналей прямокутника АВСD.
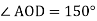
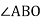
Тема 1 сам. роб. № 1
Варіант 1
- Кут між діагоналлю і стороною ромба дорівнює 200. Знайдіть кути ромба.
- Периметр прямокутника дорівнює 36 см. Знайдіть сторони прямокутника, якщо одна з них у 2 рази менша від другої.
-
О – точка перетину діагоналей прямокутника АВСD.
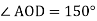
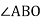
Тема 1 сам. роб. № 1
Варіант 1
- Кут між діагоналлю і стороною ромба дорівнює 200. Знайдіть кути ромба.
- Периметр прямокутника дорівнює 36 см. Знайдіть сторони прямокутника, якщо одна з них у 2 рази менша від другої.
-
О – точка перетину діагоналей прямокутника АВСD.
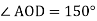
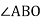
Тема 1 сам. роб. № 2
Варіант 2
- Кут ромба дорівнює 1400. Знайдіть кут між протилежною до цього кута діагоналлю і стороною ромба.
- Кути ромба відносяться, як 2:3. Знайдіть кути ромба.
-
О – точка перетину діагоналей прямокутника АВСD.
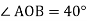
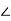
Тема 1 сам. роб. № 2
Варіант 2
- Кут ромба дорівнює 1400. Знайдіть кут між протилежною до цього кута діагоналлю і стороною ромба.
- Кути ромба відносяться, як 2:3. Знайдіть кути ромба.
-
О – точка перетину діагоналей прямокутника АВСD.
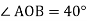
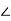
Тема 1 сам. роб. № 2
Варіант 2
- Кут ромба дорівнює 1400. Знайдіть кут між протилежною до цього кута діагоналлю і стороною ромба.
- Кути ромба відносяться, як 2:3. Знайдіть кути ромба.
-
О – точка перетину діагоналей прямокутника АВСD.
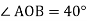
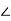
Тема 1 сам. роб. № 2
Варіант 2
- Кут ромба дорівнює 1400. Знайдіть кут між протилежною до цього кута діагоналлю і стороною ромба.
- Кути ромба відносяться, як 2:3. Знайдіть кути ромба.
-
О – точка перетину діагоналей прямокутника АВСD.
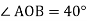
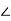
Сам. роб № 1 тема 2 Варіант 1
1. Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного.
2. Периметр трапеції дорівнює 22 см, а її бічні сторони — 4 см і 8 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на два відрізки, які відносяться як 3:8. Знайдіть основи трапеції, якщо середня лінія трапеції дорівнює 22 см.
Сам. роб № 1 тема 2 Варіант 1
1. Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного.
2. Периметр трапеції дорівнює 22 см, а її бічні сторони — 4 см і 8 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на два відрізки, які відносяться як 3:8. Знайдіть основи трапеції, якщо середня лінія трапеції дорівнює 22 см.
Сам. роб № 1 тема 2 Варіант 1
1. Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного.
2. Периметр трапеції дорівнює 22 см, а її бічні сторони — 4 см і 8 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на два відрізки, які відносяться як 3:8. Знайдіть основи трапеції, якщо середня лінія трапеції дорівнює 22 см.
Сам. роб № 1 тема 2 Варіант 1
1. Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного.
2. Периметр трапеції дорівнює 22 см, а її бічні сторони — 4 см і 8 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на два відрізки, які відносяться як 3:8. Знайдіть основи трапеції, якщо середня лінія трапеції дорівнює 22 см.
Сам. роб № 1 тема 2 Варіант 2
1. Сторони трикутника дорівнюють 4 см, 6 см і 8 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного трикутника.
2. Бічна сторона рівнобічної трапеції дорівнює 6 см, а її периметр — 34 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на 2 відрізки, один з яких в 2 рази більший від другого. Знайдіть основи трапеції, якщо її середня лінія дорівнює 21 см.
Сам. роб № 1 тема 2 Варіант 2
1. Сторони трикутника дорівнюють 4 см, 6 см і 8 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного трикутника.
2. Бічна сторона рівнобічної трапеції дорівнює 6 см, а її периметр — 34 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на 2 відрізки, один з яких в 2 рази більший від другого. Знайдіть основи трапеції, якщо її середня лінія дорівнює 21 см.
Сам. роб № 1 тема 2 Варіант 2
1. Сторони трикутника дорівнюють 4 см, 6 см і 8 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного трикутника.
2. Бічна сторона рівнобічної трапеції дорівнює 6 см, а її периметр — 34 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на 2 відрізки, один з яких в 2 рази більший від другого. Знайдіть основи трапеції, якщо її середня лінія дорівнює 21 см.
Сам. роб № 1 тема 2 Варіант 2
1. Сторони трикутника дорівнюють 4 см, 6 см і 8 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного трикутника.
2. Бічна сторона рівнобічної трапеції дорівнює 6 см, а її периметр — 34 см. Знайти середню лінію трапеції.
3. Діагональ трапеції ділить її середню лінію на 2 відрізки, один з яких в 2 рази більший від другого. Знайдіть основи трапеції, якщо її середня лінія дорівнює 21 см.
Сам. роб № 2 тема 2 Варіант 1
1. Сторони АВ, ВС та CD описаного чотирикутника відповідно дорівнюють 5 см, 6 см і 7 см. Знайдіть довжину сторони AD.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 6 : 12. Знайдіть кут ABC, якщо точка B лежить на більшій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BCA = 60°, BC = 8 см. Знайдіть радіус кола.
BCA = 60°, BC = 8 см. Знайдіть радіус кола.
Сам. роб № 2 тема 2 Варіант 1
1. Сторони АВ, ВС та CD описаного чотирикутника відповідно дорівнюють 5 см, 6 см і 7 см. Знайдіть довжину сторони AD.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 6 : 12. Знайдіть кут ABC, якщо точка B лежить на більшій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BCA = 60°, BC = 8 см. Знайдіть радіус кола.
BCA = 60°, BC = 8 см. Знайдіть радіус кола.
Сам. роб № 2 тема 2 Варіант 1
1. Сторони АВ, ВС та CD описаного чотирикутника відповідно дорівнюють 5 см, 6 см і 7 см. Знайдіть довжину сторони AD.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 6 : 12. Знайдіть кут ABC, якщо точка B лежить на більшій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BCA = 60°, BC = 8 см. Знайдіть радіус кола.
BCA = 60°, BC = 8 см. Знайдіть радіус кола.
Сам. роб № 2 тема 2 Варіант 1
1. Сторони АВ, ВС та CD описаного чотирикутника відповідно дорівнюють 5 см, 6 см і 7 см. Знайдіть довжину сторони AD.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 6 : 12. Знайдіть кут ABC, якщо точка B лежить на більшій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BCA = 60°, BC = 8 см. Знайдіть радіус кола.
BCA = 60°, BC = 8 см. Знайдіть радіус кола.
Сам. роб № 2 тема 2 Варіант 2
1. Кути A, B та C вписаного у коло чотирикутника відповідно дорівнюють 300 , 750 і 1050 . Знайдіть градусну міру кута D.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 5 : 4. Знайдіть кут ABC, якщо точка B лежить на меншій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BAС = 60°, BА = 10 см. Знайдіть радіус кола.
BAС = 60°, BА = 10 см. Знайдіть радіус кола.
Сам. роб № 2 тема 2 Варіант 2
1. Кути A, B та C вписаного у коло чотирикутника відповідно дорівнюють 300 , 750 і 1050 . Знайдіть градусну міру кута D.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 5 : 4. Знайдіть кут ABC, якщо точка B лежить на меншій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BAС = 60°, BА = 10 см. Знайдіть радіус кола.
BAС = 60°, BА = 10 см. Знайдіть радіус кола.
Сам. роб № 2 тема 2 Варіант 2
1. Кути A, B та C вписаного у коло чотирикутника відповідно дорівнюють 300 , 750 і 1050 . Знайдіть градусну міру кута D.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 5 : 4. Знайдіть кут ABC, якщо точка B лежить на меншій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BAС = 60°, BА = 10 см. Знайдіть радіус кола.
BAС = 60°, BА = 10 см. Знайдіть радіус кола.
Сам. роб № 2 тема 2 Варіант 2
1. Кути A, B та C вписаного у коло чотирикутника відповідно дорівнюють 300 , 750 і 1050 . Знайдіть градусну міру кута D.
2. Хорда AC ділить коло на дві дуги, градусні міри яких відносяться як 5 : 4. Знайдіть кут ABC, якщо точка B лежить на меншій дузі.
3. На колі позначено точки A, B і C, причому AC — діаметр кола, ![]() BAС = 60°, BА = 10 см. Знайдіть радіус кола.
BAС = 60°, BА = 10 см. Знайдіть радіус кола.
Тема 3 Сам. роб. № 1
Варіант 1
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Менша сторона другого трикутника, подібного даному, дорівнює 2,5 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔDEF. EF =14см, DF = 20 см, ВС = 21см. Знайдіть АС.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка OM, якщо ON = 4 м, OP =10 м, MK = 9 м.
Тема 3 Сам. роб. № 1
Варіант 1
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Менша сторона другого трикутника, подібного даному, дорівнює 2,5 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔDEF. EF =14см, DF = 20 см, ВС = 21см. Знайдіть АС.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка OM, якщо ON = 4 м, OP =10 м, MK = 9 м.
Тема 3 Сам. роб. № 1
Варіант 1
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Менша сторона другого трикутника, подібного даному, дорівнює 2,5 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔDEF. EF =14см, DF = 20 см, ВС = 21см. Знайдіть АС.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка OM, якщо ON = 4 м, OP =10 м, MK = 9 м.
Тема 3 Сам. роб. № 1
Варіант 1
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Менша сторона другого трикутника, подібного даному, дорівнює 2,5 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔDEF. EF =14см, DF = 20 см, ВС = 21см. Знайдіть АС.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка OM, якщо ON = 4 м, OP =10 м, MK = 9 м.
Тема 3 Сам. роб. № 1
Варіант 2
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Більша сторона другого трикутника, подібного даному, дорівнює 4 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔMKT. АВ =18 см, АС = 15см, МК = 12 см. Знайдіть МТ.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка NP, якщо OM = 3 м, OK =15 м, ON = 4 м.
Тема 3 Сам. роб. № 1
Варіант 2
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Більша сторона другого трикутника, подібного даному, дорівнює 4 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔMKT. АВ =18 см, АС = 15см, МК = 12 см. Знайдіть МТ.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка NP, якщо OM = 3 м, OK =15 м, ON = 4 м.
Тема 3 Сам. роб. № 1
Варіант 2
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Більша сторона другого трикутника, подібного даному, дорівнює 4 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔMKT. АВ =18 см, АС = 15см, МК = 12 см. Знайдіть МТ.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка NP, якщо OM = 3 м, OK =15 м, ON = 4 м.
Тема 3 Сам. роб. № 1
Варіант 2
1. Сторони трикутника дорівнюють 8 см, 6 см, 5 см. Більша сторона другого трикутника, подібного даному, дорівнює 4 см. Знайдіть решту сторін другого трикутника.
2. ΔABC ~ ΔMKT. АВ =18 см, АС = 15см, МК = 12 см. Знайдіть МТ.
3. Паралельні прямі a і b перетинають сторони кута AOB: OA у точках N і P, OB — у точках M і K відповідно. Знайдіть довжину відрізка NP, якщо OM = 3 м, OK =15 м, ON = 4 м.
Тема 3 Сам. роб. № 2
Варіант 1
1. У трикутнику АВС АВ = 16 см, АС = 20 см. На стороні АВ відклали відрізок АD = 12см, а на стороні АС — відрізок АЕ = 15 см. Чи подібні трикутники АВС і АDЕ ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють: 5 см, 8 см, 9 см і 15 см, 24 см, 27 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN =
BAN =![]() BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
Тема 3 Сам. роб. № 2
Варіант 1
1. У трикутнику АВС АВ = 16 см, АС = 20 см. На стороні АВ відклали відрізок АD = 12см, а на стороні АС — відрізок АЕ = 15 см. Чи подібні трикутники АВС і АDЕ ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють: 5 см, 8 см, 9 см і 15 см, 24 см, 27 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN =
BAN =![]() BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
Тема 3 Сам. роб. № 2
Варіант 1
1. У трикутнику АВС АВ = 16 см, АС = 20 см. На стороні АВ відклали відрізок АD = 12см, а на стороні АС — відрізок АЕ = 15 см. Чи подібні трикутники АВС і АDЕ ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють: 5 см, 8 см, 9 см і 15 см, 24 см, 27 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN =
BAN =![]() BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
Тема 3 Сам. роб. № 2
Варіант 1
1. У трикутнику АВС АВ = 16 см, АС = 20 см. На стороні АВ відклали відрізок АD = 12см, а на стороні АС — відрізок АЕ = 15 см. Чи подібні трикутники АВС і АDЕ ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють: 5 см, 8 см, 9 см і 15 см, 24 см, 27 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN =
BAN =![]() BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
BCK, AK = 0,5 см, KB = 7,5 см, BN = 5 см. Знайдіть NC.
Тема 3 Сам. роб. № 2
Варіант 2
1. У трикутнику АВС АC = 54 см, BС = 42 см. На стороні CВ відклали відрізок BD = 35 см, а на стороні АС — відрізок CN = 9 см. Чи подібні трикутники АВС і NDC ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють 9 см, 10 см, 14 см і 36 см, 40 см, 56 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN=
BAN=![]() BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
Тема 3 Сам. роб. № 2
Варіант 2
1. У трикутнику АВС АC = 54 см, BС = 42 см. На стороні CВ відклали відрізок BD = 35 см, а на стороні АС — відрізок CN = 9 см. Чи подібні трикутники АВС і NDC ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють 9 см, 10 см, 14 см і 36 см, 40 см, 56 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN=
BAN=![]() BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
Тема 3 Сам. роб. № 2
Варіант 2
1. У трикутнику АВС АC = 54 см, BС = 42 см. На стороні CВ відклали відрізок BD = 35 см, а на стороні АС — відрізок CN = 9 см. Чи подібні трикутники АВС і NDC ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють 9 см, 10 см, 14 см і 36 см, 40 см, 56 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN=
BAN=![]() BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
Тема 3 Сам. роб. № 2
Варіант 2
1. У трикутнику АВС АC = 54 см, BС = 42 см. На стороні CВ відклали відрізок BD = 35 см, а на стороні АС — відрізок CN = 9 см. Чи подібні трикутники АВС і NDC ?
2. Визначте, чи подібні трикутники, якщо їх сторони дорівнюють 9 см, 10 см, 14 см і 36 см, 40 см, 56 см.
3. У трикутнику ABC на стороні AB позначили точку K, а на стороні BC — точку N так, що ![]() BAN=
BAN=![]() BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
BCK, AK = 5 см, KB = 3 см, BN = 2 см. Знайдіть NC.
Сам. Роб № 1 Тема 4
Варіант 1
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 3 см і 12 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 5 см і 20 см
3. У прямокутному трикутнику катети дорівнюють 8см і 15см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 10см, а одна з діагоналей — 16см. Знайдіть другу діагональ ромба.
Сам. Роб № 1 Тема 4
Варіант 1
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 3 см і 12 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 5 см і 20 см
3. У прямокутному трикутнику катети дорівнюють 8см і 15см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 10см, а одна з діагоналей — 16см. Знайдіть другу діагональ ромба.
Сам. Роб № 1 Тема 4
Варіант 1
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 3 см і 12 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 5 см і 20 см
3. У прямокутному трикутнику катети дорівнюють 8см і 15см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 10см, а одна з діагоналей — 16см. Знайдіть другу діагональ ромба.
Сам. Роб № 1 Тема 4
Варіант 1
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 3 см і 12 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 5 см і 20 см
3. У прямокутному трикутнику катети дорівнюють 8см і 15см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 10см, а одна з діагоналей — 16см. Знайдіть другу діагональ ромба.
Сам. Роб № 1 Тема 4
Варіант 2
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 4 см і 9 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 9 см і 16 см
3. У прямокутному трикутнику катети дорівнюють 5см і 12см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 41см, а одна з діагоналей — 18 см. Знайдіть другу діагональ ромба.
Сам. Роб № 1 Тема 4
Варіант 2
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 4 см і 9 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 9 см і 16 см
3. У прямокутному трикутнику катети дорівнюють 5см і 12см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 41см, а одна з діагоналей — 18 см. Знайдіть другу діагональ ромба.
Сам. Роб № 1 Тема 4
Варіант 2
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 4 см і 9 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 9 см і 16 см
3. У прямокутному трикутнику катети дорівнюють 5см і 12см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 41см, а одна з діагоналей — 18 см. Знайдіть другу діагональ ромба.
Сам. Роб № 1 Тема 4
Варіант 2
1. Знайдіть висоту прямокутного трикутника, якщо її основа ділить гіпотенузу на відрізки 4 см і 9 см.
2. Знайдіть катет прямокутного трикутника, якщо його проекція на гіпотенузу і гіпотенуза відповідно дорівнюють 9 см і 16 см
3. У прямокутному трикутнику катети дорівнюють 5см і 12см. Знайдіть периметр трикутника.
4. Сторона ромба дорівнює 41см, а одна з діагоналей — 18 см. Знайдіть другу діагональ ромба.
Сам. Роб № 2 Тема 4
Варіант 1
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 5 см і 13 см. Знайдіть синус гострого кута, який лежить проти меншого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 6 см, а бічна сторона – 5 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Сам. Роб № 2 Тема 4
Варіант 1
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 5 см і 13 см. Знайдіть синус гострого кута, який лежить проти меншого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 6 см, а бічна сторона – 5 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Сам. Роб № 2 Тема 4
Варіант 1
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 5 см і 13 см. Знайдіть синус гострого кута, який лежить проти меншого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 6 см, а бічна сторона – 5 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Сам. Роб № 2 Тема 4
Варіант 1
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 5 см і 13 см. Знайдіть синус гострого кута, який лежить проти меншого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 6 см, а бічна сторона – 5 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Сам. Роб № 2 Тема 4
Варіант 2
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 6 см і 10 см. Знайдіть синус гострого кута, який лежить проти більшого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 10 см, а бічна сторона – 13 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Сам. Роб № 2 Тема 4
Варіант 2
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 6 см і 10 см. Знайдіть синус гострого кута, який лежить проти більшого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 10 см, а бічна сторона – 13 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Сам. Роб № 2 Тема 4
Варіант 2
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 6 см і 10 см. Знайдіть синус гострого кута, який лежить проти більшого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 10 см, а бічна сторона – 13 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Сам. Роб № 2 Тема 4
Варіант 2
1. Катет і гіпотенуза прямокутного трикутника відповідно дорівнюють 6 см і 10 см. Знайдіть синус гострого кута, який лежить проти більшого катета.
2. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
3. Основа рівнобедреного трикутника дорівнює 10 см, а бічна сторона – 13 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника.
Тема 5 сам. роб. № 1
Варіант 1
1. Чому дорівнює сума кутів опуклого семикутника?
2. Знайдіть площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, — 7 см.
3. Знайдіть площу рівнобедреного трикутника, бічна сторона якого дорівнює 15 см, а висота, проведена до основи, — 9 см.
4. Периметр прямокутника дорівнює
40 см, а одна з його сторін дорівнює 4 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 1
Варіант 1
1. Чому дорівнює сума кутів опуклого семикутника?
2. Знайдіть площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, — 7 см.
3. Знайдіть площу рівнобедреного трикутника, бічна сторона якого дорівнює 15 см, а висота, проведена до основи, — 9 см.
4. Периметр прямокутника дорівнює
40 см, а одна з його сторін дорівнює 4 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 1
Варіант 1
1. Чому дорівнює сума кутів опуклого семикутника?
2. Знайдіть площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, — 7 см.
3. Знайдіть площу рівнобедреного трикутника, бічна сторона якого дорівнює 15 см, а висота, проведена до основи, — 9 см.
4. Периметр прямокутника дорівнює
40 см, а одна з його сторін дорівнює 4 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 1
Варіант 1
1. Чому дорівнює сума кутів опуклого семикутника?
2. Знайдіть площу паралелограма, сторона якого дорівнює 12 см, а висота, проведена до неї, — 7 см.
3. Знайдіть площу рівнобедреного трикутника, бічна сторона якого дорівнює 15 см, а висота, проведена до основи, — 9 см.
4. Периметр прямокутника дорівнює
40 см, а одна з його сторін дорівнює 4 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 1
Варіант 2
1. Чому дорівнює сума кутів опуклого восьмикутника?
2. Знайдіть площу ромба, діагоналі якого дорівнюють 10 см і 16 см.
3. Основа рівнобедреного трикутника дорівнює 16см, а бічна сторона — 17 см. Знайдіть площу трикутника.
4. Периметр прямокутника дорівнює
26 см, а одна з його сторін дорівнює 9 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 1
Варіант 2
1. Чому дорівнює сума кутів опуклого восьмикутника?
2. Знайдіть площу ромба, діагоналі якого дорівнюють 10 см і 16 см.
3. Основа рівнобедреного трикутника дорівнює 16см, а бічна сторона — 17 см. Знайдіть площу трикутника.
4. Периметр прямокутника дорівнює
26 см, а одна з його сторін дорівнює 9 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 1
Варіант 2
1. Чому дорівнює сума кутів опуклого восьмикутника?
2. Знайдіть площу ромба, діагоналі якого дорівнюють 10 см і 16 см.
3. Основа рівнобедреного трикутника дорівнює 16см, а бічна сторона — 17 см. Знайдіть площу трикутника.
4. Периметр прямокутника дорівнює
26 см, а одна з його сторін дорівнює 9 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 1
Варіант 2
1. Чому дорівнює сума кутів опуклого восьмикутника?
2. Знайдіть площу ромба, діагоналі якого дорівнюють 10 см і 16 см.
3. Основа рівнобедреного трикутника дорівнює 16см, а бічна сторона — 17 см. Знайдіть площу трикутника.
4. Периметр прямокутника дорівнює
26 см, а одна з його сторін дорівнює 9 см. Знайдіть сторону квадрата, рівновеликого прямокутнику.
Тема 5 сам. роб. № 2
Варіант 1
1. Основи трапеції дорівнюють 8 см і 4 см, а її висота — 3 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 64,8 см2, одна основа – 15 см, а інша – на 3 см менше від неї.
3. У рівнобедреній трапеції АВСМ більша основа АМ=20см, ВН - висота, АН=6см,
![]()
![]()
Тема 5 сам. роб. № 2
Варіант 1
1. Основи трапеції дорівнюють 8 см і 4 см, а її висота — 3 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 64,8 см2, одна основа – 15 см, а інша – на 3 см менше від неї.
3. У рівнобедреній трапеції АВСМ більша основа АМ=20см, ВН - висота, АН=6см,
![]()
![]()
Тема 5 сам. роб. № 2
Варіант 1
1. Основи трапеції дорівнюють 8 см і 4 см, а її висота — 3 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 64,8 см2, одна основа – 15 см, а інша – на 3 см менше від неї.
3. У рівнобедреній трапеції АВСМ більша основа АМ=20см, ВН - висота, АН=6см,
![]()
![]()
Тема 5 сам. роб. № 2
Варіант 1
1. Основи трапеції дорівнюють 8 см і 4 см, а її висота — 3 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 64,8 см2, одна основа – 15 см, а інша – на 3 см менше від неї.
3. У рівнобедреній трапеції АВСМ більша основа АМ=20см, ВН - висота, АН=6см,
![]()
![]()
Тема 5 сам. роб. № 2
Варіант 2
1. Основи трапеції дорівнюють 12 см і 6 см, а її висота — 5 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 77 см2, одна основа – 13 см, а інша – на 4 см менше від неї.
3. Знайти площу рівнобедреної трапеції ABCD, якщо висота BH = 9см, основа ВС =9см, а відрізок AH = 3 см.
Тема 5 сам. роб. № 2
Варіант 2
1. Основи трапеції дорівнюють 12 см і 6 см, а її висота — 5 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 77 см2, одна основа – 13 см, а інша – на 4 см менше від неї.
3. Знайти площу рівнобедреної трапеції ABCD, якщо висота BH = 9см, основа ВС =9см, а відрізок AH = 3 см.
Тема 5 сам. роб. № 2
Варіант 2
1. Основи трапеції дорівнюють 12 см і 6 см, а її висота — 5 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 77 см2, одна основа – 13 см, а інша – на 4 см менше від неї.
3. Знайти площу рівнобедреної трапеції ABCD, якщо висота BH = 9см, основа ВС =9см, а відрізок AH = 3 см.
Тема 5 сам. роб. № 2
Варіант 2
1. Основи трапеції дорівнюють 12 см і 6 см, а її висота — 5 см. Знайдіть площу трапеції.
2. Знайдіть висоту трапеції, якщо її площа дорівнює 77 см2, одна основа – 13 см, а інша – на 4 см менше від неї.
3. Знайти площу рівнобедреної трапеції ABCD, якщо висота BH = 9см, основа ВС =9см, а відрізок AH = 3 см.
-
Дякую!
-
-


про публікацію авторської розробки
Додати розробку
